Арккосинус

О.Функциявозрастает наи принимает все значения отдо, значит по теореме о корнев промежуткеуравнениеимеет единственный корень.

Это число называетсяарккосинусомчислаи обозначается.

Т.е. арккосинусомчисланазывается такое число из промежутка, косинус которого равен: .

Так как функция на промежуткестрого убывает, значит, по теореме об обратной функции, она имеет обратную функцию:, переобозначив переменные, получаем

Рассмотрим свойстваэтой функции:

1. Область определения функции:

.

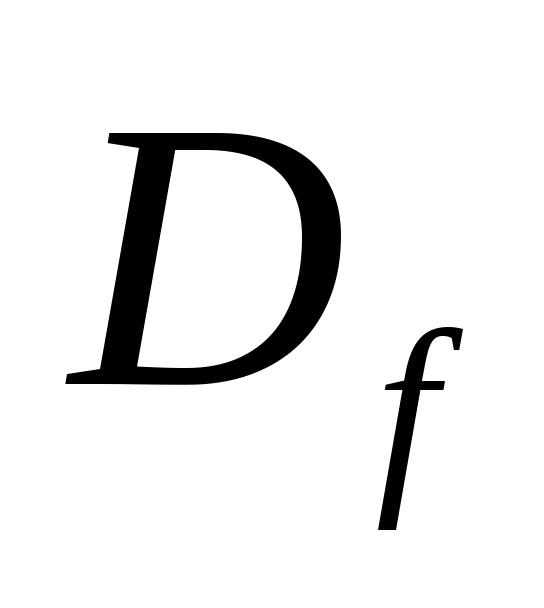
2. Множество значений функции:

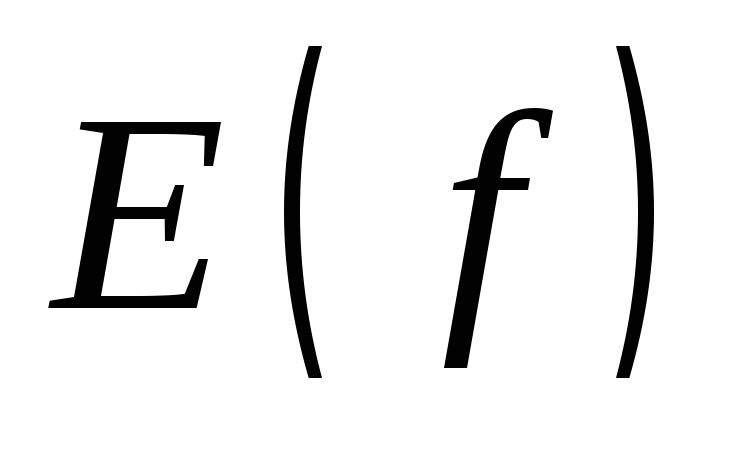
3. Периодичность:

Функция не периодическая, так как она строго убывает на всей области определения (по теореме об обратной функции)

Чётность/нечётность

Из рисунка 21 видно, что , т.е. функцияне является ним четной, ни нечетной.

4. Точки пересечения графика с осями координат.

С осью : если

С осью

5. Промежутки знакопостоянства функции:

В силу того, что функция убывает на и, то

6. Интервалы возрастания/убывания

По теореме об обратной функции, так как функцияубывает на, следовательно убывает на.

7. Наибольшее/наименьшее значение функции

Так как функция строго возрастает на всей области определения и непрерывна, то

8. График функции

(рис 22).

Арктангенс

О.Функциявозрастает наи принимает все действительные значения. Поэтому,, такого, чтопо теореме о корне уравнениеимеет единственный корень.

Это число называетсяарктангенсомчислаи обозначается.

Т.е. арктангенсомчисланазывается такое число из промежутка, тангенс которого равен: .

Так как функцияна промежуткестрого возрастает, значит, по теореме об обратной функции, она имеет обратную функцию:, переобозначив переменные, получаем

Рассмотрим свойстваэтой функции:

1. Область определения функции:

.

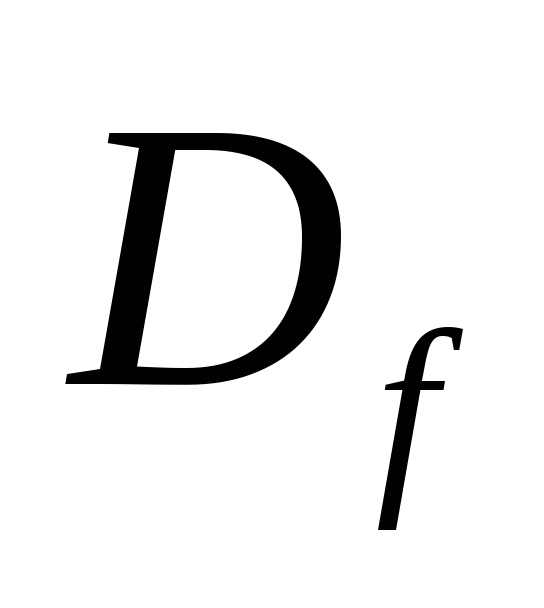
2. Множество значений функции:

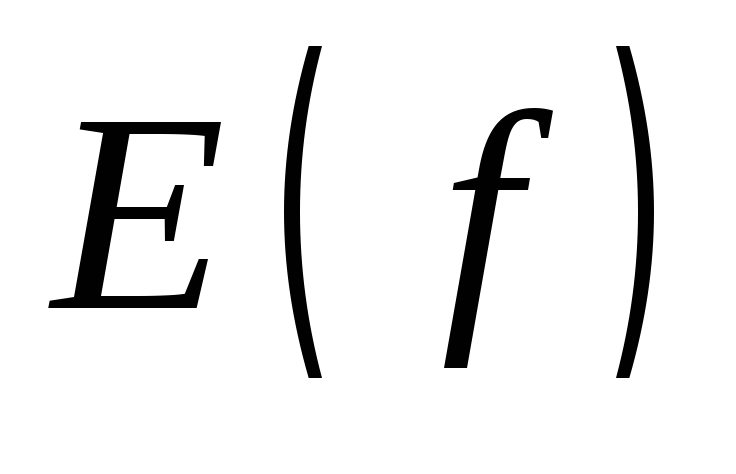
3. Периодичность:

Функция не периодическая, так как она строго возрастает на всей области определения (по теореме об обратной функции)

4. Чётность/нечётность

Из рисунка 23 видно, что , т.е. функциянечетная

5. Точки пересечения графика с осями координат.

С осью : если

С осью

6. П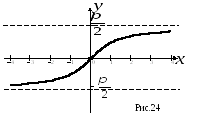ромежутки знакопостоянства функции:

:

7. Интервалы возрастания/убывания

По теореме об обратной функции, так как функциявозрастает на, следовательно возрастает на всей области определения.

8. Наибольшее/наименьшее значение функции

Так как , то функция не имеет ни наибольшего, ни наименьшего значений.

9. График функции. График функции 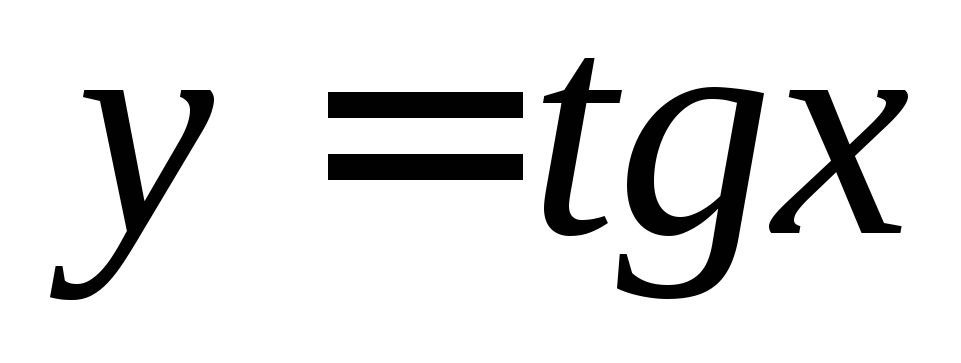имеет горизонтальные асимптоты:. (рис 24).

Арккотангенс

О.Функцияубывает наи принимает все действительные значения, поэтому,, такого, чтопо теореме о корне, уравнениеимеет единственный корень.

Это число называетсяарккотангенсомчислаи обозначается.

Т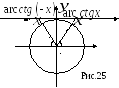.е.арккотангенсомчисланазывается такое число из промежутка, тангенс которого равен: .

Т.е. арккосинусомчисланазывается такое число из промежутка, котангенс которого равен: .

Так как функция на промежуткестрого убывает, значит, по теореме об обратной функции, она имеет обратную функцию:, переобозначив переменные, получаем

Рассмотрим свойстваэтой функции:

1. Область определения функции:

.

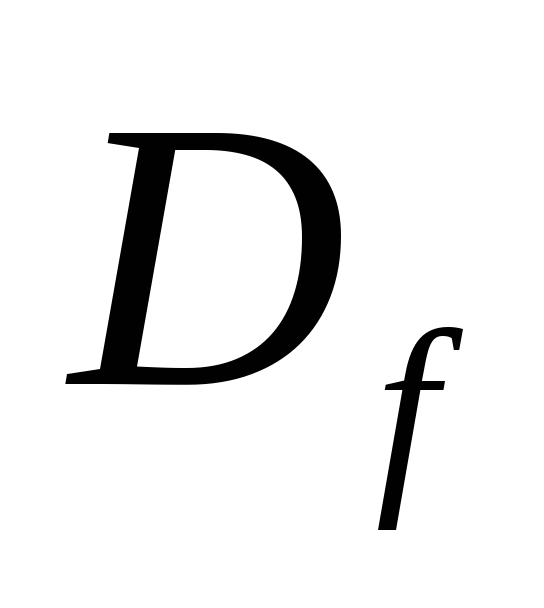
2. Множество значений функции:

3. Периодичность:

Функция не периодическая, так как она строго убывает на всей области определения (по теореме об обратной функции)

4. Чётность/нечётность

Из рисунка 25 видно, что , т.е. функцияне является ним четной, ни нечетной.

5. Точки пересечения графика с осями координат.

С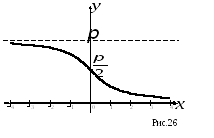осью: если

С осью

6. Промежутки знакопостоянства функции:

В силу того, что функция убывает на всей области определения и , тона всей области определения.

7. Интервалы возрастания/убывания

По теореме об обратной функции, так как функцияубывает наследовательно убывает на всей области определения.

8. Наибольшее/наименьшее значение функции

Так как, то функция не имеет ни наибольшего, ни наименьшего значений.

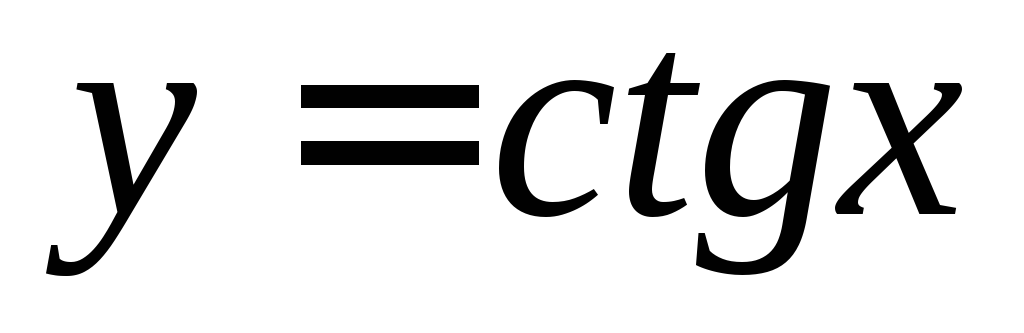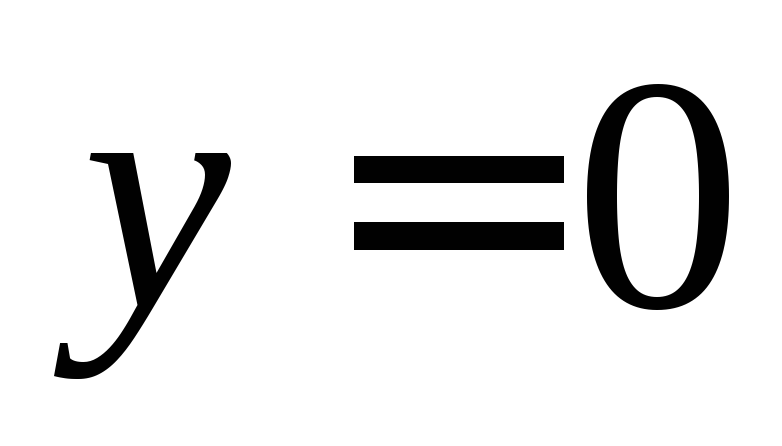9. График функции. График функции имеет горизонтальные асимптоты:и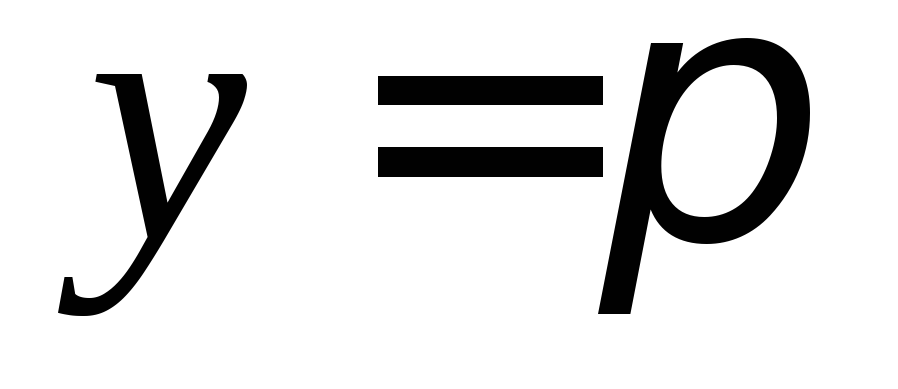. (рис 26).