21. Формулы приведения.

Тригонометрические функции углов вида ,,,могут быть выражены через функции углас помощью формул, которые называютсяформулами приведения.

Формулы приведения предназначены для того, чтобы выражать значения тригонометрических функций произвольных углов через функции острого угла.

В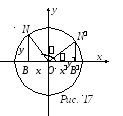се приводимые ниже формулы справедливы при произвольных значениях угла(естественно, входящих в область определения соответствующих функций), хотя применяются преимущественно в тех случаях, когда угол – острый.

Докажем сначала, что для любого

и

Для определённости предположим, что . Тогда для угласправедливо двойное неравенство. Рассмотрим радиусыи, образующие углыис положительным направлением осисоответственно (рис. 17). Опустим из точекиперпендикуляры на ось. Полученные треугольникииравны, поскольку они прямоугольные,, имеют равные гипотенузы () и равные острые углы:.

Из равенства треугольников следует, что и.Следовательно,, . Вторая формула получается с помощью аналогичных рассуждений.

Для тангенса и котангенса формулы приведения следуют из равенств

и .

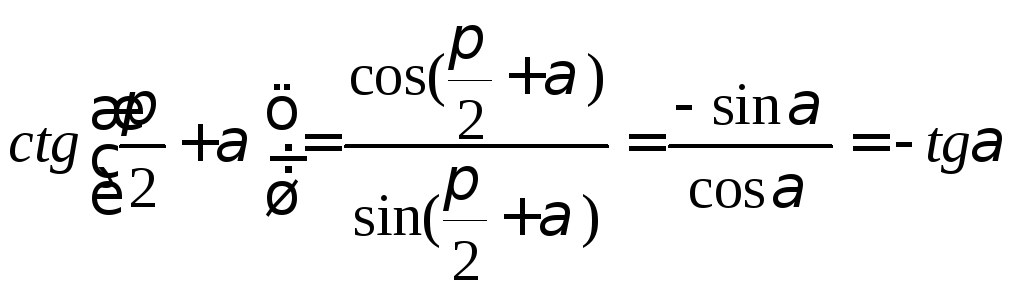Из формул , а также с учётом чётности и нечётности тригонометрических функций можно получить формулы

, ,,.

Например, .

Формулы приведения для синуса и косинуса угла выглядят так:

и .

Для доказательства достаточно представить в видеи дважды воспользоваться формулами. Аналогичные формулы для тангенса и котангенса,можно получить с помощью формул приведения для синуса и косинуса.

Из формул (3) следует:

, ,,. (20.4)

Для доказательства достаточно представить в виде суммыи применить формулы (20.3).

Формулы приведения для углов имеют вид

, ,,.

Для доказательства этих формул надо представить и последовательно применить формулы (20.3) и (20.1).

Справедливы также формулы

, ,,.

Перечисленные выше формулы могут быть обобщены одним правилом:

Любая тригонометрическая функция угла по абсолютной величине равна той же функции угла, если числоn - чётное, и ко-функции этого же угла, если n – нечётное.

При этом если функция угла положительна, когда– острый положительный угол, то знаки обеих функций одинаковы; если отрицательна, то различны.

22. Зависимости между тригонометрическими функциями одного и того же аргумента

Теорема (основное тригонометрическое тождество).

Для любого угла справедливо тождество.

Доказательство.

П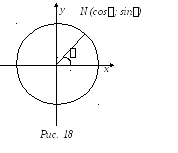усть дан некоторый угол. Тогда координаты конца радиуса тригонометрического круга, составляющего уголс положительным направлением оси, будут равны по определению, (рис.18). Так как квадрат расстояния между любыми двумя точками плоскости, заданными своими координатами, равен сумме квадратов разностей одноимённых координат, то квадрат расстояния от точкидо точки(равный единице, поскольку- конец радиуса единичной длины) определяется равенством,

откуда следует .

Между основными тригонометрическими функциями произвольного аргумента αимеются следующие соотношения.

1. Основное тригонометрическое тождество

.

Доказательство тождества приведено выше.

2. По определению тангенса и котангенса выполнено

, для ,;

, для ,.

3. Перемножая последние два соотношения, получим

для ,.

4. Разделив основное тригонометрическое тождество почленно наии выполнив несложные преобразования, получим соответственно

для ,.

Аналогично для,.