
- •§2. Свободный вектор
- •§3. Сложение и вычитание свободных векторов
- •§4. Умножение свободного вектора на число
- •Лекция 2. Векторное пространство. Базис и координаты вектора §5. Понятие векторного пространства
- •§6. Линейная зависимость векторов
- •§7. Базис векторного пространства. Координаты вектора
- •Лекция 3. Скалярное умножение свободных векторов §8. Проекция вектора на вектор
- •§9. Скалярное умножение свободных векторов
- •Лекция 4 - 5. Векторное и смешанное умножение свободных векторов §10. Ориентация векторного пространства
- •§11. Векторное умножение свободных векторов
- •§12. Смешанное умножение свободных векторов
- •Раздел II. Аналитическая планиметрия Лекция 1. Аффинные системы координат на плоскости. Метод координат §1. Аффинная система координат на плоскости
- •§2. Формулы преобразования координат
- •§3. Метод координат на плоскости
- •Лекция 2. Прямая на плоскости как линия первого порядка §4. Уравнение прямой на плоскости
- •§5. Особенности расположения прямой относительно системы координат
- •Лекция 3. Аналитическое задание полуплоскостей. Вычисление расстояний и углов на плоскости §6. Геометрический смысл знака трехчлена прямой
- •§7. Расстояние от точки до прямой
- •§8. Взаимное расположение двух прямых на плоскости
- •§9. Угол между прямыми
- •Лекция 4. Конические сечения: эллипс, гипербола, парабола §10. Эллипс
- •§11. Гипербола
- •§12. Парабола
- •§13. Директориальное свойство эллипса и гиперболы
- •Лекция 5. Классификация линий второго порядка на плоскости §14. Приведение общего уравнения линии второго порядка к каноническому виду
- •Лекция 6. Общая теория линий второго порядка §15. Центр линии второго порядка
- •§16. Взаимное расположение линии второго порядка и прямой
- •§19. Диаметры линий второго порядка
- •§20. Главные направления, главные диаметры
- •Литература
§5. Особенности расположения прямой относительно системы координат
Относительно
системы координат
![]() прямая
прямая![]() задана уравнением
задана уравнением![]() ,
где
,
где![]() .
.
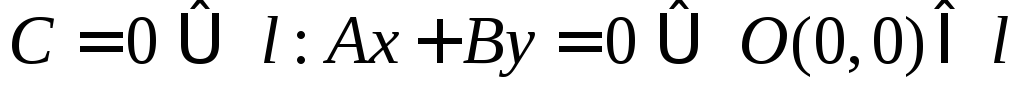 ;
;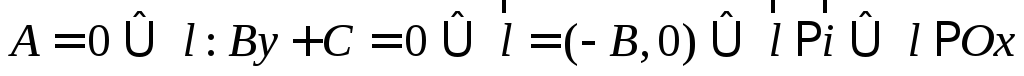 ;
;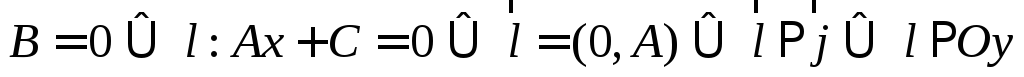 ;
;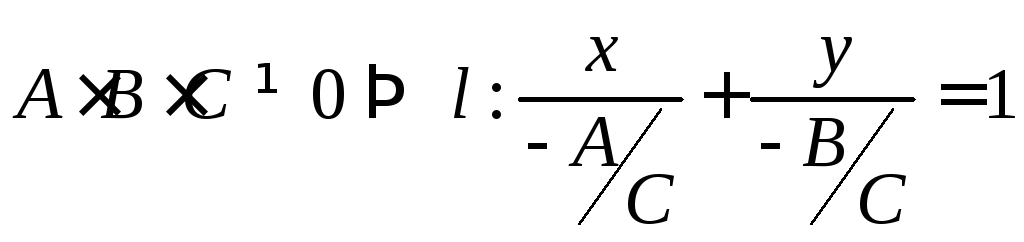 или
или
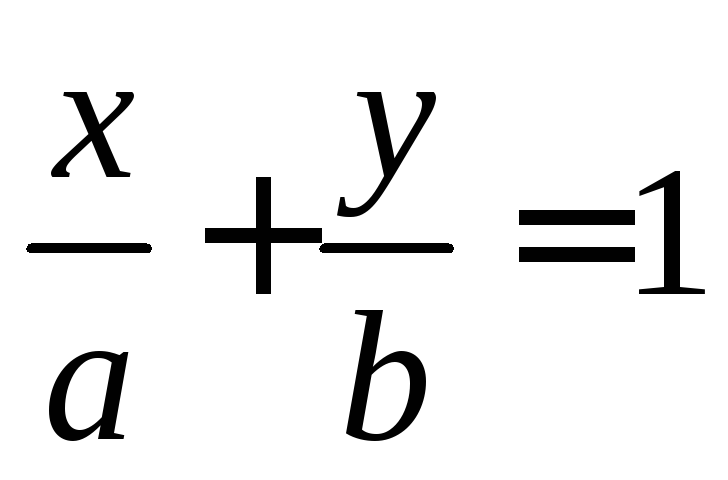 –уравнение
прямой в отрезках.
–уравнение
прямой в отрезках.
Здесь
![]() и
и![]() – отрезки, отсекаемые прямой на
координатных осях.
– отрезки, отсекаемые прямой на
координатных осях.
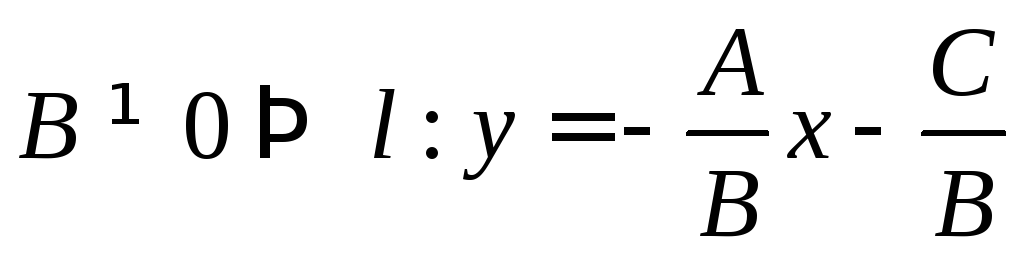 или
или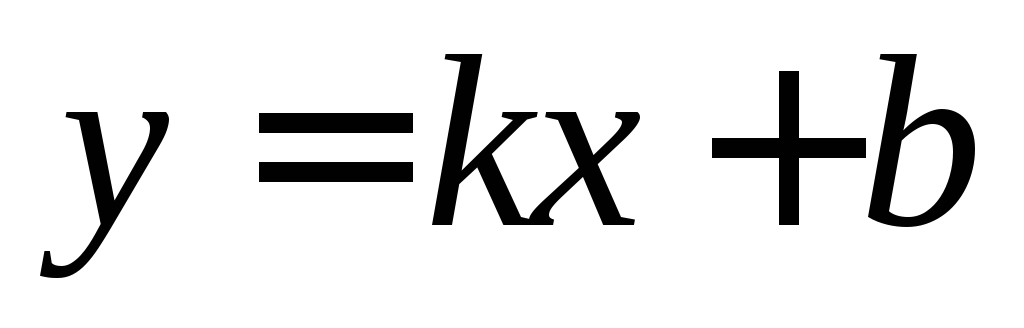 –уравнение
прямой с угловым коэффициентом.
Здесь
–уравнение
прямой с угловым коэффициентом.
Здесь
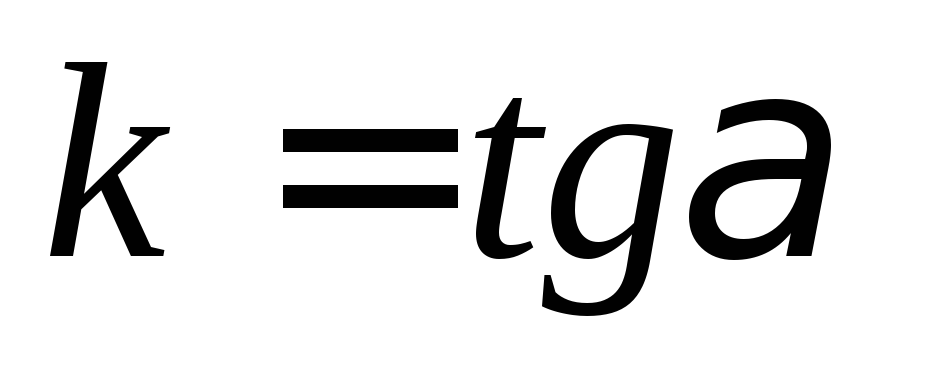 – тангенс угла наклона прямой к оси
– тангенс угла наклона прямой к оси .
.
Лекция 3. Аналитическое задание полуплоскостей. Вычисление расстояний и углов на плоскости §6. Геометрический смысл знака трехчлена прямой
Каждая прямая плоскости разделяет эту плоскость на две части, называемые полуплоскостями. Две точки одной и той же полуплоскости лежат по одну сторону от данной прямой. Любые две точки, принадлежащие различным полуплоскостям, лежат по разные стороны от прямой. Как аналитически, то есть по уравнению прямой и координатам точек определить, лежат эти точки в одной или в разных полуплоскостях относительно данной прямой?
Относительно
аффинной системы координат
![]() прямая задана уравнением
прямая задана уравнением![]() ,
где
,
где![]() .
.
Обозначим
![]() –трехчлен
прямой.
–трехчлен
прямой.
Для
точек
![]() и
и![]() ,
не лежащих на прямой
,
не лежащих на прямой![]() ,
будем иметь
,
будем иметь![]() .
.
Точки
![]() и
и![]() лежат по разные стороны от прямой
лежат по разные стороны от прямой![]() тогда и только тогда, когда отрезок
тогда и только тогда, когда отрезок![]() пересекает прямую
пересекает прямую![]() в некоторой точке
в некоторой точке![]() .
.
Так
как точка
![]() лежит между
лежит между![]() и
и![]() ,
то
,
то![]() и
и![]() ,
,![]() .
.
Точка
![]() лежит на прямой
лежит на прямой![]() ,
поэтому
,
поэтому![]() .
Отсюда получаем
.
Отсюда получаем![]() и
и![]() ,
а значит
,
а значит![]() и
и![]() разных знаков.
разных знаков.
Таким
образом, две точки
![]() и
и![]() лежат по разные стороны от прямой
лежат по разные стороны от прямой![]() тогда и только тогда, когда значения
трехчлена прямой для координат этих
точек
тогда и только тогда, когда значения
трехчлена прямой для координат этих
точек![]() и
и![]() разных знаков.
разных знаков.
Имеем геометрический смысл знака трехчлена:
Каждое
из неравенств
![]() определяет полуплоскость с границей
определяет полуплоскость с границей![]() .
.
§7. Расстояние от точки до прямой
Пусть
на плоскости относительно прямоугольной
системы координат
![]() прямая
прямая![]() задается уравнением
задается уравнением![]() ,
где
,
где![]() .
.
Расстояние
от точки
![]() до прямой
до прямой![]() равняется длине перпендикуляра
равняется длине перпендикуляра![]() ,
проведенного из
,
проведенного из![]() к прямой
к прямой![]() .
.
Так
как
![]() ,
то
,
то![]() .
.
![]() .
Так как
.
Так как![]() равен
либо 1, либо -1, то получаем
равен
либо 1, либо -1, то получаем
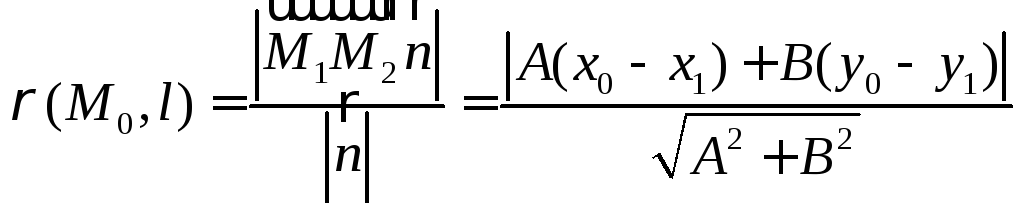 .
Учитывая, что
.
Учитывая, что
![]() ,
то есть
,
то есть![]() ,
получаемформулу
для вычисления расстояния от точки до
прямой
,
получаемформулу
для вычисления расстояния от точки до
прямой
![]() .
.
§8. Взаимное расположение двух прямых на плоскости
Относительно
аффинной системы координат![]() прямые
прямые![]() и
и![]() задаются уравнениями
задаются уравнениями
![]()
Для каждой прямой можно найти точку, принадлежащую этой прямой, и направляющий вектор
![]()
![]()
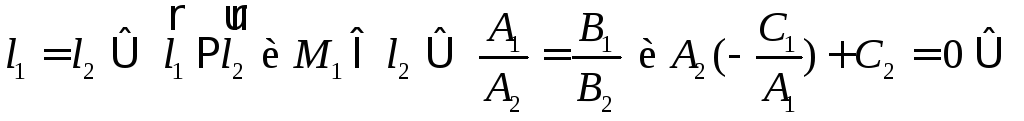
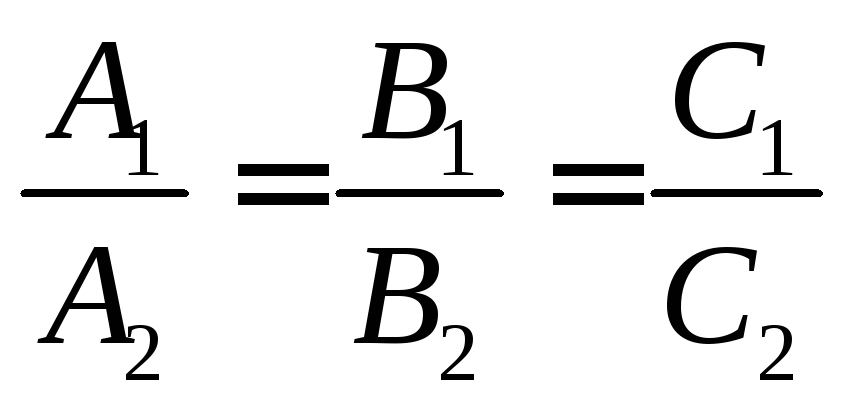
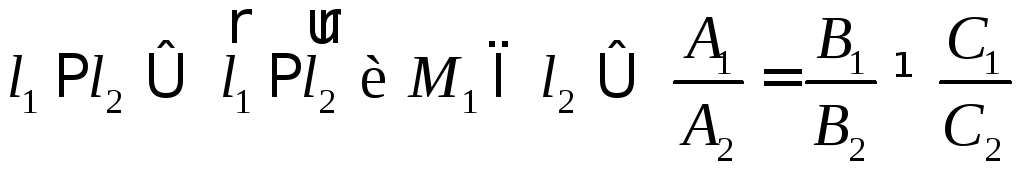 .
. .
.
§9. Угол между прямыми
Углом
между прямыми
![]() и
и![]() называется величина того из четырех
вертикальных углов, образованных этими
прямыми, который не превосходит остальные
углы. Таким образом, угол
называется величина того из четырех
вертикальных углов, образованных этими
прямыми, который не превосходит остальные
углы. Таким образом, угол![]() между прямыми может принимать значения
от 0 до
между прямыми может принимать значения
от 0 до![]() .
.
Иногда
удобно угол между прямыми считать
направленным. Угол между прямыми
![]() и
и![]() ,
заданными в указанном порядке, будем
считать положительным, если поворот от
,
заданными в указанном порядке, будем
считать положительным, если поворот от![]() к
к![]() по этому углу совершается против часовой
стрелки, в противном случае угол будем
считать отрицательным.
по этому углу совершается против часовой
стрелки, в противном случае угол будем
считать отрицательным.
Пусть
на плоскости относительно прямоугольной
системы координат
![]() прямые
прямые![]() и
и![]() задаются уравнениями
задаются уравнениями
![]()
Тогда
![]() ,
,![]() .
.
Угол
 между прямыми
между прямыми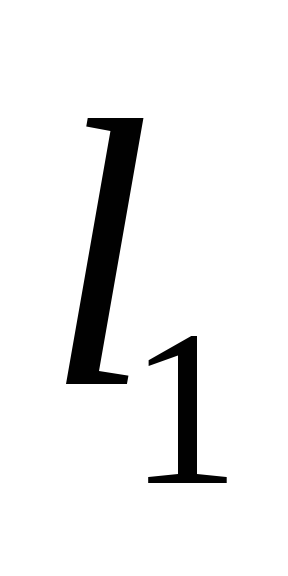 и
и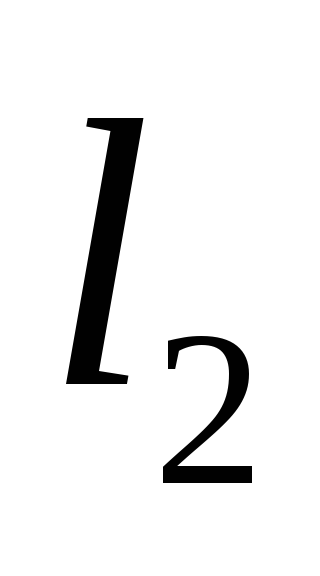 равен
равен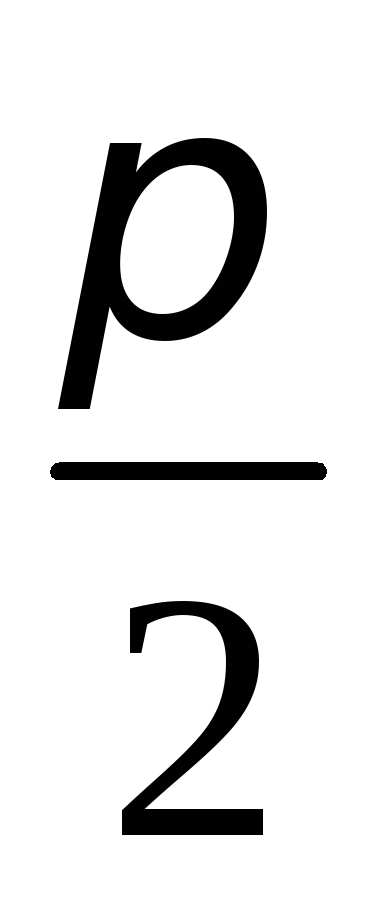 тогда и только тогда, когда направляющие
векторы прямых ортогональны и,
следовательно,
тогда и только тогда, когда направляющие
векторы прямых ортогональны и,
следовательно,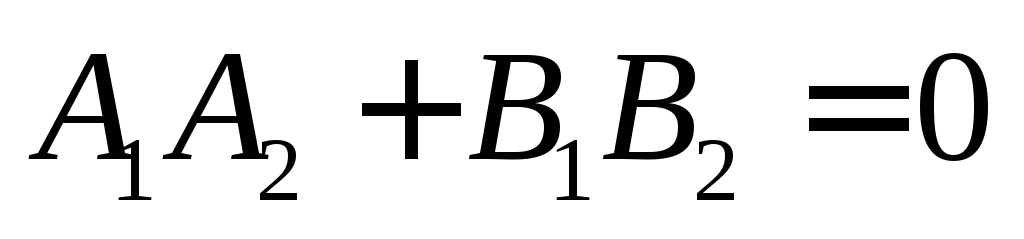 .
.Если угол
 между прямыми отличен от
между прямыми отличен от ,
то он однозначно определяется по
значению его тангенса.
Можно заметить,
что тангенс направленного угла между
прямыми равен тангенсу направленного
угла между направляющими векторами
этих прямых
,
то он однозначно определяется по
значению его тангенса.
Можно заметить,
что тангенс направленного угла между
прямыми равен тангенсу направленного
угла между направляющими векторами
этих прямых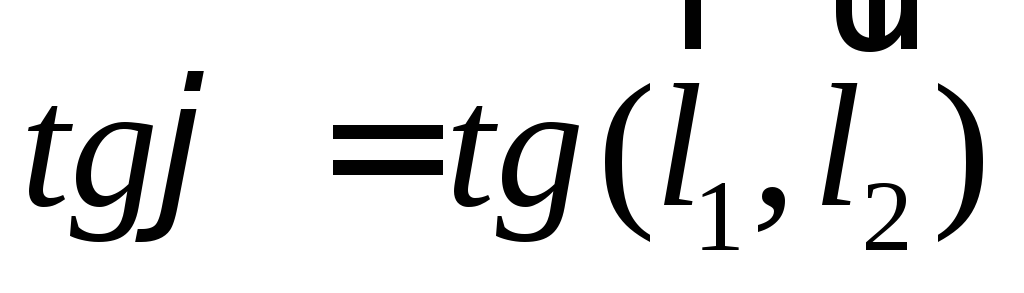 .
.
Как
вычислить тангенс направленного угла
![]() между векторами
между векторами![]() и
и![]() ?
?
Пусть
![]() и
и![]() направленные
углы между вектором
направленные
углы между вектором![]() и направляющими векторами прямых. Для
направленного угла
и направляющими векторами прямых. Для
направленного угла![]() между векторами
между векторами![]() и
и![]() имеем
имеем![]() .
.
Для
вычисления
![]() найдем
найдем![]() и
и![]() :
:
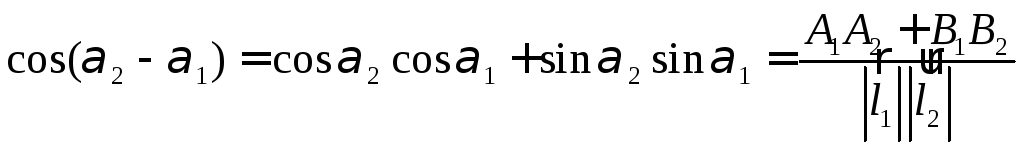 .
.
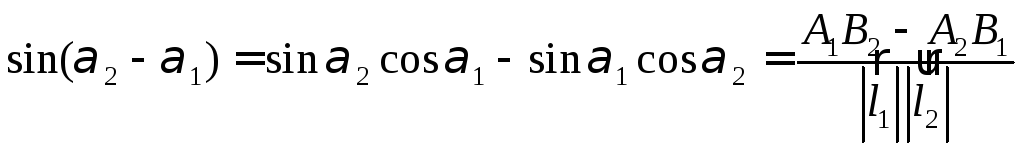 .
.
Таким
образом,
![]() .
.
Возможны случаи
а)
![]() .
.
![]() ,
где
,
где
![]() и
и![]() – угловые коэффициенты прямых
– угловые коэффициенты прямых![]() и
и![]() .
.
б)
![]() ,
(
,
(![]() параллельна, а
параллельна, а![]() не параллельна оси
не параллельна оси![]() ).
).
![]() .
.
в)
![]() (
(![]() параллельна, а
параллельна, а![]() не параллельна оси
не параллельна оси![]() ).
).
![]() .
.
г)
![]() ,
(прямые параллельны оси
,
(прямые параллельны оси![]() ).
).
