Лекция 6. Общая теория линий второго порядка §15. Центр линии второго порядка

Пусть относительно аффинной системы координат линиявторого порядка задана уравнением

(1)

О п р е д е л е н и е. Центром линии второго порядка называется точка, координаты которой удовлетворяют системе

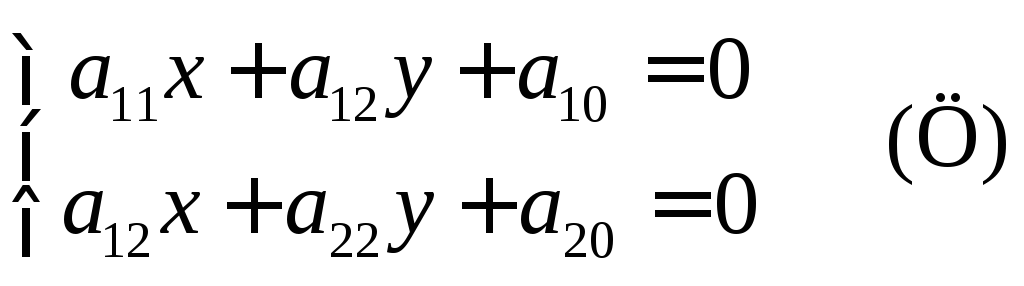
Число центров линии второго порядка зависит от определителя системы (Ц):

• Если 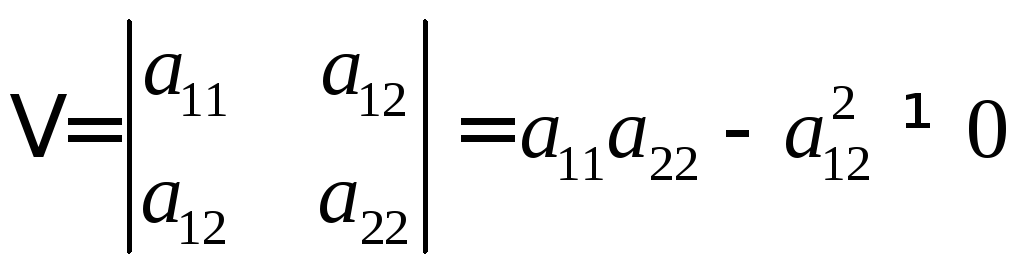, то система (Ц) имеет единственное решение, то есть линияимеет единственный центр и называетсяцентральной линией. Можно проверить, что эллипс, мнимый эллипс, гипербола, пара пересекающихся прямых, пара мнимых пересекающихся прямых являются центральными линиями.

• Если 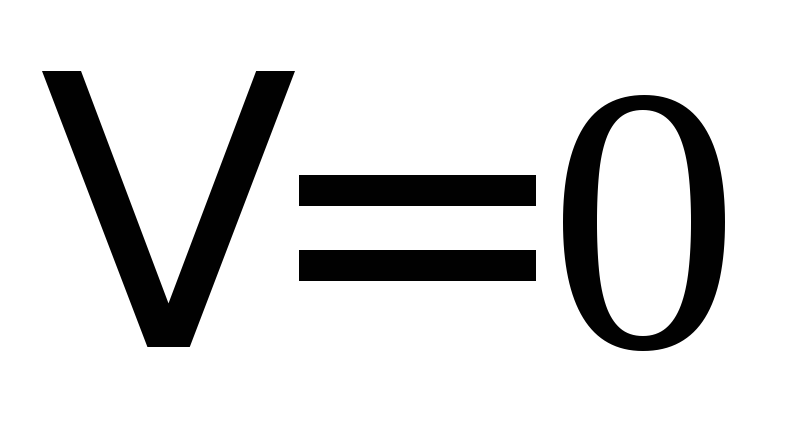, то система (Ц) либо имеет бесконечно много решений, либо не имеет решений. Соответственно линия второго порядка либо имеет бесконечно много центров (пара параллельных прямых, пара мнимых параллельных прямых, пара совпавших прямых), либо не имеет центра (парабола).

Перенеся начало репера в точку– центр линии, получим уравнение этой линии в репере:

, из которого видно, что точка – центр линии второго порядка, является центром симметрии линии.

§16. Взаимное расположение линии второго порядка и прямой

Пусть относительно аффинной системы координат линиявторого порядка задана уравнением

(1),

прямая задана параметрическими уравнениями

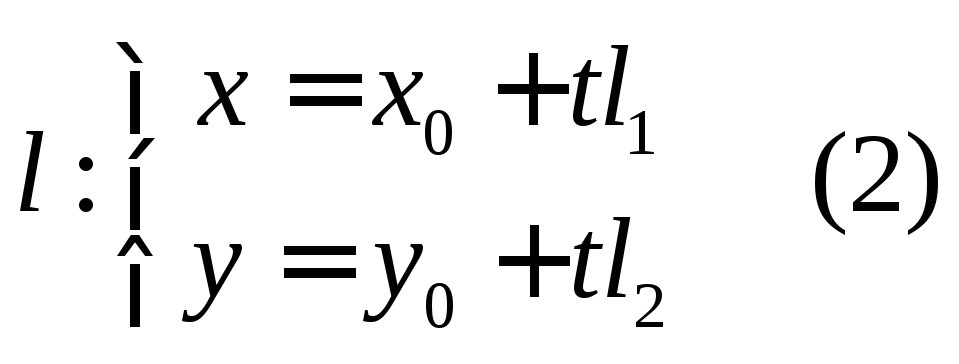
Пересечение прямой и линии второго порядка находится из системы уравнений (1) и (2). Подставляя (2) в (1), получим

где

Возможны случаи:

I. , (*) – квадратное уравнение с дискриминантом.

а) . Уравнение (*) имеет два вещественных корня и прямаяпересекает линиюв двух вещественных точках.

б) . Уравнение (*) имеет два одинаковых корня, прямая пересекает линию второго порядка в двух совпавших точках.

в) . Уравнение (*) имеет два мнимых комплексно сопряженных корня, прямая пересекает линию второго порядка в двух мнимых комплексно сопряженных точках.

II. , то есть. Уравнение (*) принимает вид.

а) . Уравнение (*) имеет единственный корень, прямая пересекает линию второго порядка в одной точке.

б) . Уравнение (*) не имеет корней, прямая не пересекает линию второго порядка.

в) . Уравнение (*) становится тождеством, то есть любая точка прямой лежит на линии второго порядка, прямая является частью линии второго порядка.

О п р е д е л е н и е. Направление, определяемое ненулевым вектором, называется асимптотическим направлением относительно линии второго порядка, если любая прямая, параллельная этому направлению, имеет с линией второго порядка не более одной общей точки, или является частью этой линии.

Из предыдущих рассуждений получаем, что направление, определяемое ненулевым вектором , является асимптотическим относительно линии второго порядка тогда и только тогда, когда. Таким образом, имеем условие асимптотического направления:

.

Сколько может быть асимптотических направлений относительно линии второго порядка?

Заметим, что для определения направления, определяемого вектором достаточно знать отношение координат этого вектора.

I. . В этом случае и из условия (А) получаем, что(в противном случае получаем, что). Из уравнения (А) получаем квадратное уравнение относительно, дискриминант которого . То есть это уравнение не имеет корней, а значит, относительно линии второго порядка нет асимптотических направлений. В этом случае линия называется линией эллиптического типа. Можно проверить, что эллипс, мнимый эллипс, пара мнимых пересекающихся прямых – линии эллиптического типа.

II. .

а) . В этом случае (А) имеет вид. Имеем два асимптотических направления относительно линии второго порядка, определяемые векторамии.

б) . Из уравнения (А) следует, что. Имеем квадратное уравнение, дискриминант которого больше нуля. То есть это уравнение имеет два различных корня, а значит, относительно линии второго порядка существует ровно два асимптотических направления. В этом случае линия называетсялинией гиперболического типа. Можно проверить, что гипербола, пара пересекающихся прямых – линии гиперболического типа.

III. . Рассмотрев случаи, когда равно или не равно нулю, получим, что относительно линии второго порядка существует ровно одно асимптотическое направление. В этом случае линия второго порядка называетсялинией параболического типа. Убедитесь, что парабола, пара параллельных, пара мнимых параллельных и пара совпавших прямых являются линиями параболического типа.

О п р е д е л е н и е. Прямая называется касательной к линии второго порядка, если она пересекает эту линию в двух совпавших точках.

Из предыдущих рассуждений следует, что прямая, задаваемая уравнением (2), является касательной к линии второго порядка , еслии.

Выбрав в качестве начальной точки для прямойточку касания, получим. Тогда, то есть

.

Тогда в качестве направляющего вектора прямой можно выбрать вектор с координатами

.

Каноническое уравнение касательной в точке линии второго порядка будет иметь вид

.

У п р а ж н е н и е. Найти уравнение касательной к эллипсу, гиперболе, параболе, заданным каноническими уравнениями.