
- •§2. Свободный вектор
- •§3. Сложение и вычитание свободных векторов
- •§4. Умножение свободного вектора на число
- •Лекция 2. Векторное пространство. Базис и координаты вектора §5. Понятие векторного пространства
- •§6. Линейная зависимость векторов
- •§7. Базис векторного пространства. Координаты вектора
- •Лекция 3. Скалярное умножение свободных векторов §8. Проекция вектора на вектор
- •§9. Скалярное умножение свободных векторов
- •Лекция 4 - 5. Векторное и смешанное умножение свободных векторов §10. Ориентация векторного пространства
- •§11. Векторное умножение свободных векторов
- •§12. Смешанное умножение свободных векторов
- •Раздел II. Аналитическая планиметрия Лекция 1. Аффинные системы координат на плоскости. Метод координат §1. Аффинная система координат на плоскости
- •§2. Формулы преобразования координат
- •§3. Метод координат на плоскости
- •Лекция 2. Прямая на плоскости как линия первого порядка §4. Уравнение прямой на плоскости
- •§5. Особенности расположения прямой относительно системы координат
- •Лекция 3. Аналитическое задание полуплоскостей. Вычисление расстояний и углов на плоскости §6. Геометрический смысл знака трехчлена прямой
- •§7. Расстояние от точки до прямой
- •§8. Взаимное расположение двух прямых на плоскости
- •§9. Угол между прямыми
- •Лекция 4. Конические сечения: эллипс, гипербола, парабола §10. Эллипс
- •§11. Гипербола
- •§12. Парабола
- •§13. Директориальное свойство эллипса и гиперболы
- •Лекция 5. Классификация линий второго порядка на плоскости §14. Приведение общего уравнения линии второго порядка к каноническому виду
- •Лекция 6. Общая теория линий второго порядка §15. Центр линии второго порядка
- •§16. Взаимное расположение линии второго порядка и прямой
- •§19. Диаметры линий второго порядка
- •§20. Главные направления, главные диаметры
- •Литература
Министерство образования и науки РФ
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
«Уральский государственный педагогический университет»
Толстопятов В.П.
ГЕОМЕТРИЯ
Курс лекций 1 семестр
Учебное пособие
Екатеринбург
2012
Геометрия. Курс лекций 1 семестр/ Учебное пособие / Урал. гос. пед. ун-т. – Екатеринбург, 2012. – 60 с.
Толстопятов В.П., к.ф.-м.н., профессор кафедры геометрии УрГПУ
Уральский государственный
педагогический университет, 2012
СОДЕРЖАНИЕ
Раздел I. Элементы векторной алгебры 4
Раздел II. Аналитическая планиметрия 18
Литература 47
Раздел I. Элементы векторной алгебры
Лекция 1. Свободный вектор. Линейные операции над свободными векторами
§1. Направленные отрезки
Рассматриваем геометрическое пространство, которое изучалось в школьном курсе геометрии.
О
п р е д е л е н и е.
Отрезок называется направленным,
если указан порядок его концов.
Обозначение:
![]() .
.
О
п р е д е л е н и е. Направленные отрезки
![]() и
и![]() называютсясонаправленными
(противоположно
направленными), если
лучи
называютсясонаправленными
(противоположно
направленными), если
лучи
![]() и
и![]() сонаправлены (противоположно направлены).
сонаправлены (противоположно направлены).
О
п р е д е л е н и е. Направленные отрезки
![]() и
и![]() называютсяпротивоположными.
называютсяпротивоположными.
О п р е д е л е н и е. Пару совпавших точек будем называть нулевым направленным отрезком.
О
п р е д е л е н и е. Длиной
направленного отрезка
![]() назовем длину отрезка
назовем длину отрезка![]() .
.
§2. Свободный вектор
О
п р е д е л е н и е .Свободным
вектором
![]() называется множество всех сонаправленных
отрезков одинаковой длины.
называется множество всех сонаправленных
отрезков одинаковой длины.
Если
направленный отрезок
![]() принадлежит вектору
принадлежит вектору![]() ,
то говорят, что
,
то говорят, что![]() –представитель вектора
–представитель вектора
![]() .
Чтобы задать свободный вектор, достаточно
указать какой-либо его представитель,
поэтому записывают
.
Чтобы задать свободный вектор, достаточно
указать какой-либо его представитель,
поэтому записывают![]() .
.
Запись
![]() означает, что направленные отрезки
означает, что направленные отрезки![]() и
и![]() имеют одинаковую длину и сонаправлены.
имеют одинаковую длину и сонаправлены.
Все
нулевые направленные отрезки образуют
нулевой вектор ![]() .
.
О
п р е д е л е н и е. Длиной
свободного вектора
![]() называется длина любого его представителя.
называется длина любого его представителя.
Из определения свободного вектора вытекают следующие два свойства:
![]() (упорядоченная пара точек
однозначно определяет вектор);
(упорядоченная пара точек
однозначно определяет вектор);
![]() (от каждой точки можно отложить
вектор).
(от каждой точки можно отложить
вектор).
У
п р а ж н е н и е. Доказать свойство
![]() .
.
О
п р е д е л е н и е. Вектор
![]() параллелен прямой
параллелен прямой
![]() ,
если его представители параллельны
прямой
,
если его представители параллельны
прямой![]() или лежат на этой прямой. Нулевой вектор
считается параллельным любой прямой.
или лежат на этой прямой. Нулевой вектор
считается параллельным любой прямой.
О
п р е д е л е н и е. Векторы
![]() и
и![]() называютсяколлинеарными
(
называютсяколлинеарными
(![]() ),
если они параллельны одной прямой.
),
если они параллельны одной прямой.
О
п р е д е л е н и е. Пусть
![]() .
Если представители этих векторов
сонаправлены (противоположно направлены),
то ивекторы сонаправлены
(противоположно
направлены):
.
Если представители этих векторов
сонаправлены (противоположно направлены),
то ивекторы сонаправлены
(противоположно
направлены):
![]() ,
,![]() .
.
Очевидно, два вектора равны тогда и только тогда, когда они сонаправлены и их длины равны.
О
п р е д е л е н и е. Противоположно
направленные векторы
![]() и
и![]() одинаковой длины называютсяпротивоположными
векторами. Записывают
одинаковой длины называютсяпротивоположными
векторами. Записывают
![]() .
.
О
п р е д е л е н и е. Три вектора
![]() ,
,![]() ,
,![]() называютсякомпланарными,
если их представители лежат в одной
плоскости или параллельны этой плоскости.
называютсякомпланарными,
если их представители лежат в одной
плоскости или параллельны этой плоскости.
Очевидно, что если два из трех векторов коллинеарны, то эти три вектора компланарны.
§3. Сложение и вычитание свободных векторов
О
п р е д е л е н и е. Сумма
свободных векторов
![]() и
и![]() определяется по «правилу треугольника».
Отложим от точки
определяется по «правилу треугольника».
Отложим от точки![]() вектор
вектор![]() ,
равный вектору
,
равный вектору![]() .
От точки
.
От точки![]() отложим вектор
отложим вектор![]() ,
равный вектору
,
равный вектору![]() .
Вектор
.
Вектор![]() назовем суммой векторов
назовем суммой векторов![]() и
и![]() .
.
Из определения суммы векторов следует свойство:
![]() (аксиома
треугольника).
(аксиома
треугольника).
У п р а ж н е н и е. Доказать теорему о независимости суммы свободных векторов от выбора начальной точки.
У п р а ж н е н и е. Доказать законы сложения векторов:
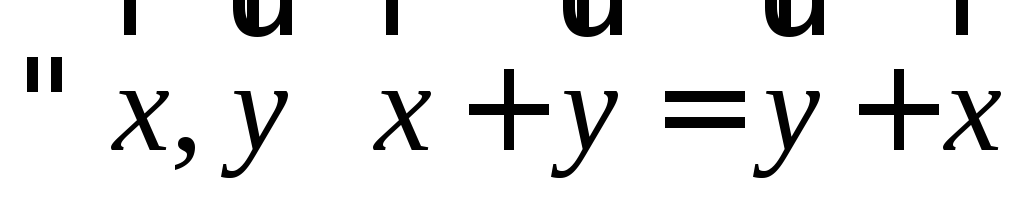 (переместительный закон или
коммутативность);
(переместительный закон или
коммутативность);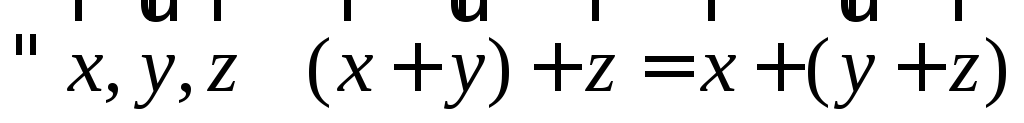 (сочетательный закон или
ассоциативность);
(сочетательный закон или
ассоциативность);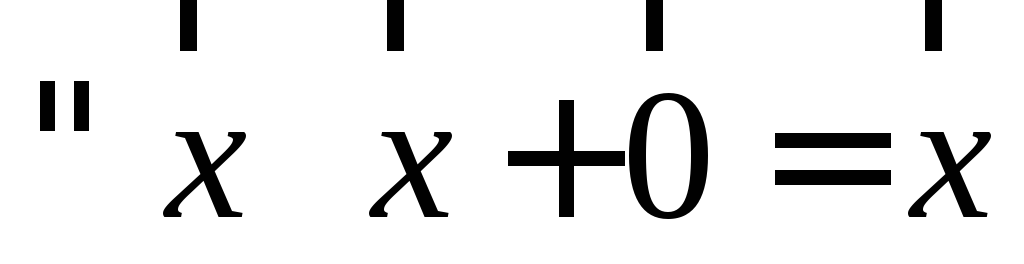 ;
;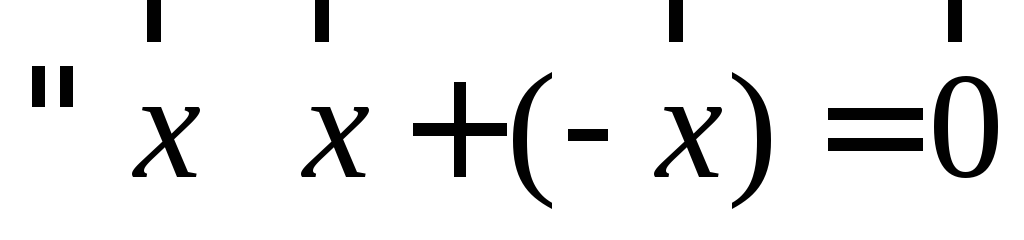 .
.
О
п р е д е л е н и е. Разностью
свободных векторов
![]() и
и![]() называется такой вектор
называется такой вектор![]() ,
что
,
что![]() .
.
Прибавив
к обеим частям равенства
![]() вектор
вектор![]() ,
получим
,
получим![]() .
Таким образом, чтобы вычесть из вектора
.
Таким образом, чтобы вычесть из вектора![]() вектор
вектор![]() ,
нужно к
,
нужно к![]() прибавить вектор, противоположный
вектору
прибавить вектор, противоположный
вектору![]() .
.
Полезно
запомнить, что если два вектора отложены
от одной точки, то вектор, соединяющий
их концы, является разностью этих
векторов. Причем из того вектора, где
сходятся две стрелочки, вычитают второй
вектор:
![]() .
.
§4. Умножение свободного вектора на число
О
п р е д е л е н и е. Произведением
свободного вектора
![]() на действительное число
на действительное число
![]() называется свободный вектор
называется свободный вектор![]() ,
длина которого равна произведению
модуля числа
,
длина которого равна произведению
модуля числа![]() на длину вектора
на длину вектора![]() ,
и этот вектор сонаправлен с вектором
,
и этот вектор сонаправлен с вектором![]() ,
если число
,
если число![]() неотрицательное, и противоположно
направлен, если число
неотрицательное, и противоположно
направлен, если число![]() отрицательное.
отрицательное.
У п р а ж н е н и е. Доказать законы умножения вектора на число:
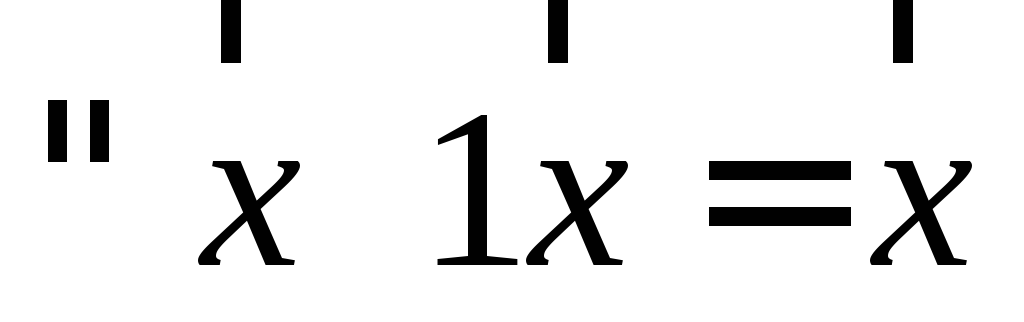 ;
;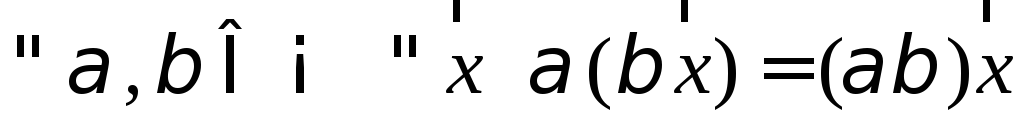 ;
;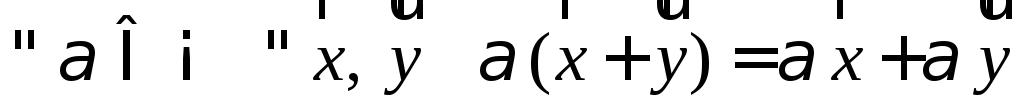 ;
;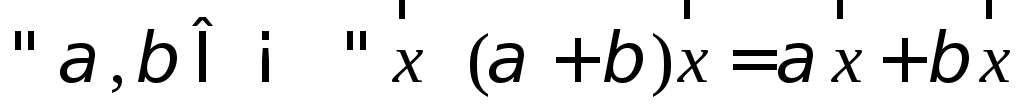 .
.
У п р а ж н е н и е. Доказать условие коллинеарности двух векторов:
Два вектора коллинеарны тогда и только тогда, когда они отличаются друг от друга числовым множителем.
О
п р е д е л е н и е. Выражение
![]() называютлинейной
комбинацией векторов
называютлинейной
комбинацией векторов
![]() .
.
Ясно, что результатом линейной комбинации векторов является вектор.
Доказанные законы сложения векторов и умножения вектора на число, позволяют применять к линейным комбинациям векторов все правила преобразований, установленные в алгебре для многочленов первой степени. Можно приводить подобные; раскрывать скобки; выносить за скобку; переносить с противоположным знаком из одной части равенства в другую; умножать обе части равенства на одно и то же число.
