Построение тренда

Построим тренд по 30 данным.

Формула	R2	Коэффициент Тейла
Linear Y=10,5285+2,46805*t	99,63	0,0242
Square root-Y Y=(4,00091+0,177668*t)2	95,48	0,0551
Multiplicative Y=8,86971*t0,1643202	94,60	0,0996
Square root-X Y=-18,6898+18,3435*sqrt(t)	88,79	0,0729

Перестроим модель вида y=a+b*t тренда по 35 данным:

10,2919+2,4895*t

Дисперсия	2,33
Среднее квадратическое отклонение	1,53
Значение Т-статистики	2,04

Найдем доверительные интервалы для прогноза и оценок модели:

9,183911,41

2,422,55

t(34, 0,05)=2,04

Доверительный интервал: 96,60103,21

ПРОВЕРКА ГИПОТЕЗЫ О ПРАВИЛЬНОСТИ ВЫБОРА ВИДА ТРЕНДА

Проверка гипотезы о правильности выбора вида тренда заключается в том, что отклонения от тренда будут носить случайный характер.

Критерий серий (основанный на медиане выборки)

Рассчитаем отклонения от тренда ₁,₂, … ,₃₀ , отсортировав, найдем медианное значение. Рассмотрим исходный ряд отклонений и сравним полученные значения с медианным _мед по следующему правилу

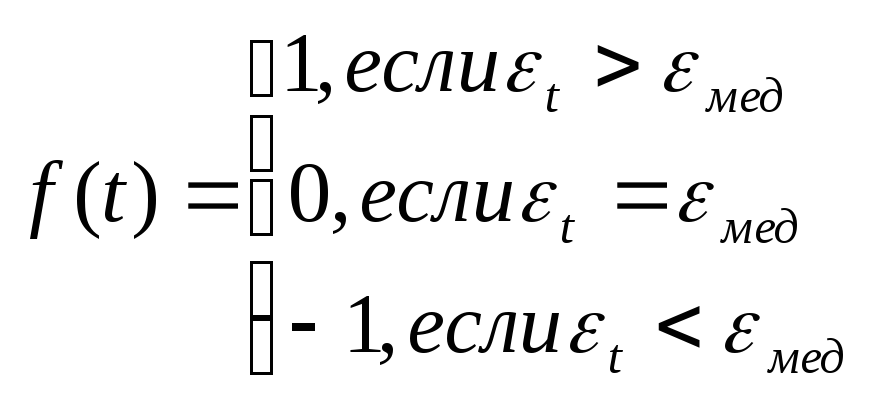
Последовательность идущих подряд 1 или –1 называется серией. Если отклонения от тренда случайные, то чередование серий должно быть также случайным. Для аналитической оценки случайности отклонений используют следующий метод: подсчитывают длину самой длинной серии К_мах(30) и общее число серий (30). Выборка признается случайной если выполняются следующие неравенства (для 5% уровня значимости):

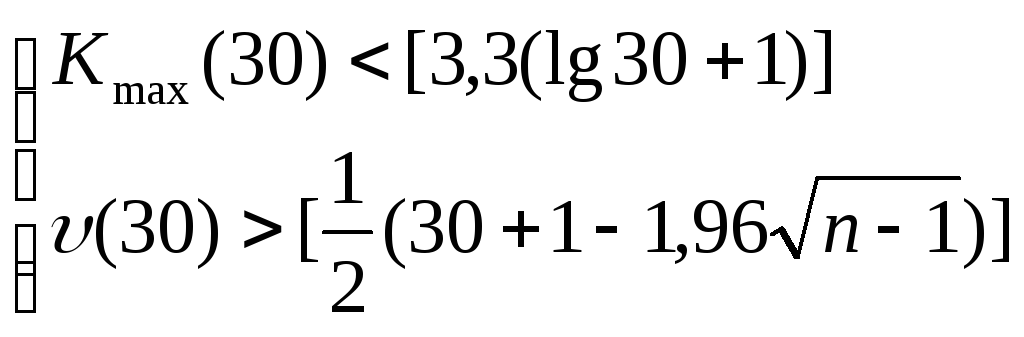
В результате расчетов получили, что медиана _мед = -2,15,

K_max(30) = 6 < 8,175

(30) = 23 > 10,223.

Таким образом, отклонение уравнений временного ряда от тренда случайно, и уравнение тренда составлено правильно.

ПРОВЕРКА ГИПОТЕЗЫ О СТАЦИОНАРНОСТИ СЛУЧАЙНОГО КОМПОНЕНТА

Основным условием стационарности случайного процесса является зависимость автокорреляционной функции только от разности аргументов

t_i – t_j = . На практике ориентируются на   n / 4, в нашем случае  = 7.

Для проверки гипотезы о том, что значение автокорреляционной функции зависит не от выбора начала отсчета наблюдений, а только от величины сдвига , найдем для случайного компонента _t (t = 1, …, 30) значения автокорреляционной функции . Затем, исключив последнее наблюдение найдем новую автокорреляционную функцию , и так далее, исключая k (k = 0, 1, …, K) наблюдений, получим  = 7 групп, содержащих по K + 1 коэффициентов автокорреляции, так как рассматриваемый ряд наблюдений содержит 30 значений, то возьмем К=10, большее количество брать не целесообразно, т.к. ряд не будет коротким и полученные коэффициенты не будут адекватными реальной ситуации.

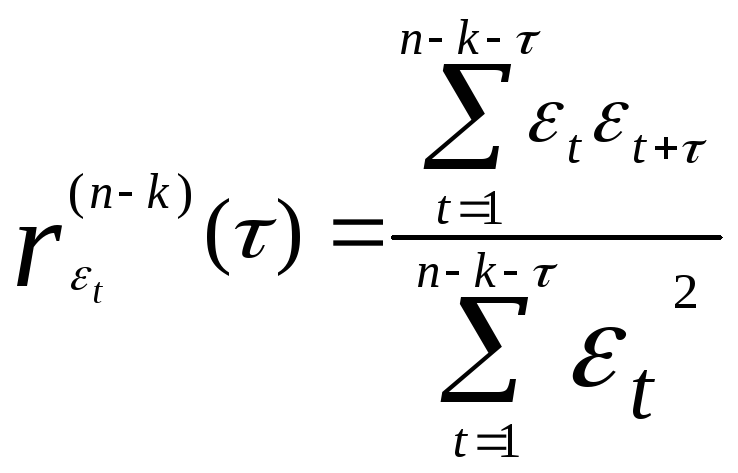
Для стационарного в широком смысле случайного процесса коэффициенты автокорреляции, входящие в одну и ту же группу должны быть однородными.

Для проверки на однородность для каждого из вычисляют величину z-критерия 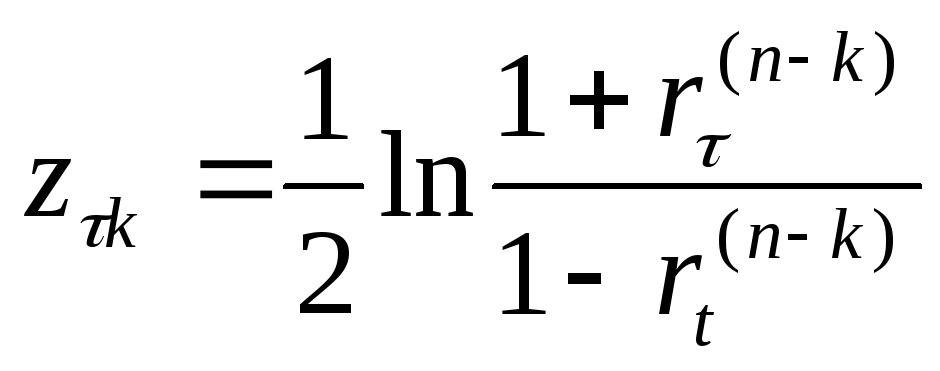, затем рассчитывают для каждой группы 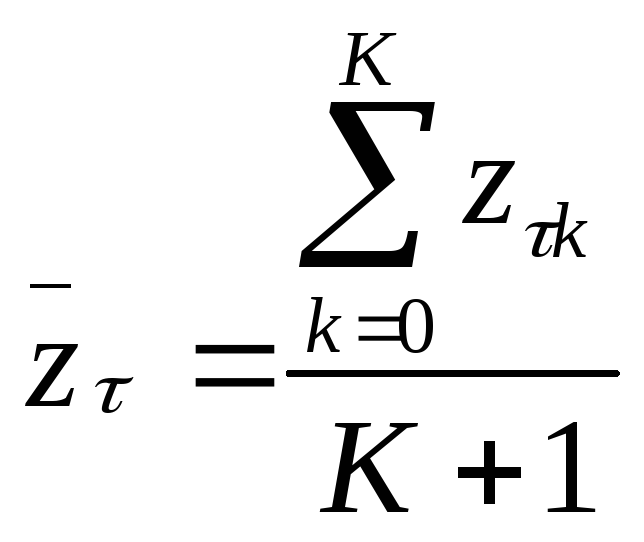. Далее для каждой группы рассчитывается значение 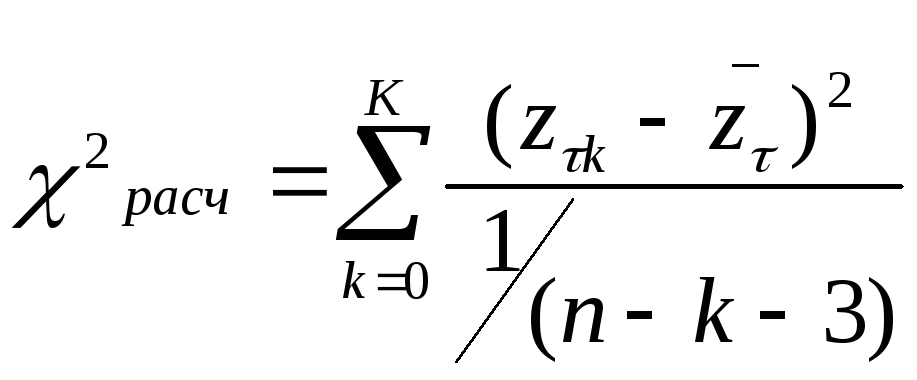, которое сравнивается табличным ² (K).

Если ²_расч < ² (K), то гипотеза об однородности -й группы не отвергается. Если гипотеза об однородности не отвергается для всех групп, то можно принять, что автокорреляционная функция зависит не от начала отсчета, а только от разности t_i – t_j = , т.е. случайный компонент представляет собой стационарный в широком смысле случайный процесс.

Таблица коэффициентов автокорреляции и Z-критерий представлена в приложении №1.

Приведем результаты расчетов ²_расч .

	 = 1	 = 2	 = 3	 = 4	 = 5	 = 6	 = 7	2(0.05, 10)
2расч	0,307	0,174	2,549	0,83	0,621	0,771	0,456	18.3

Таким образом, можно предположить, что отклонения от линейного тренда являются стационарным в широком смысле случайным процессом.

Для наглядности построим коррелограмму, которая в будущем может использоваться для выбора глубины авторегрессионной модели.

ОПРЕДЕЛЕНИЕ НАЛИЧИЯ АВТОКОРРЕЛЯЦИИ В ИСХОДНОМ РЯДУ С ПОМОЩЬЮ КРИТЕРИЯ ДАРБИНА-УОТСЕНА

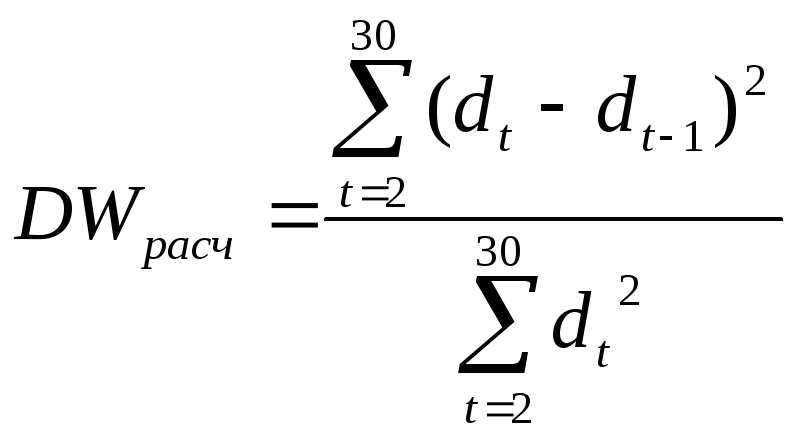, где d_t = y_t - y_t^p. Из данной формулы с помощью преобразований можно получить, что DW[0;4]. Причем при DW = 0 – положительная автокорреляция, DW = 2 – нет автокорреляции, DW = 4 – отрицательная автокорреляция.

Полученное значение сравнивается с табличными верхним d_h и нижним d_l значениями, выбираемыми при уровне значимости , числе факторов в модели  и числе членов временного ряда n.

Могут иметь место следующие случаи:

DW < d_l – положительная автокорреляция;

d_h < DW < 4 - d_h – отсутствие автокорреляции;

DW > 4 – d_l – отрицательная автокорреляция;

d_l < DW < d_h или 4 - d_h < DW < 4 – d_l – нет статистических оснований принять или отвергнуть гипотезу об отсутствии автокорреляции.

В результате расчетов получили, что DW = 3.0005; при  = 0.05,  = 1,

n = 30 - d_l = 1.35 , d_h = 1.49. Тогда 4 – d_l = 2.65, 4 – d_h = 2.61.

В рассматриваемом случае DW > 4 – d_l – отрицательная автокорреляция, поэтому можно переходить к построению авторегрессионой модели.