
НИРС / НИРС ЛР№2. Отчет
.pdf[Введите текст]
Министерство образования Российской Федерации ФГОУ ВПО Поволжский государственный технологический университет
Кафедра РТиМБС
Отчет по лабораторной работе №2
СТАТИСТИЧЕСКИЕ ФУНКЦИИ МАТКАДА
по дисциплине Научно-исследовательская работа студентов
Выполнил: студент РСК-21 Рахмаев А.О.
Проверил: ст. преподаватель Охотников С.А.
Йошкар-Ола, 2013
Рахмаев АО РСК-21
Оглавление сюда

Рахмаев АО РСК-21
Лабораторная работа № 2 Статистические функции маткада
Цель: Получить навыки построения законов распределений с помощью встроенных функций MathCAD. Рассмотреть основные задачи математической статистики и методы их решения в системе MathCAD.
Теория
В Маткаде существуют целый набор встроенных функций для вычисления числовых характеристик случайной величины. К ним относятся:
1.mean (A) – возвращает среднее значение вектора А.
2.cvar(A,B) – возвращает корреляционный момент случайных векторов А и В.
3. stdev(A) – возвращает стандартное (среднеквадратическое) отклонение элементов вектора A.
4.corr(vx,vy) –возвращает коэффициент корреляции векторов vx vy. 5. hist (i,v)- функция построение гистограммы.
В Маткаде имеется целый ряд встроенных функций, позволяющих строить законы распределения случайных величин. К ним, в частности, относятся функции:
1) dnorm(x,μ,σ)- плотность вероятности для нормального распределения. Здесь x- случайная величина, μ – ее математическое ожидание, σ- среднеквадратическое отклонение.
Выражение для нормального закона распределения имеет вид,
где m – математическое ожидание, а σ – среднеквадратическое отклонение случайной величины х.
2)dunif(x,a,b)- равномерная плотность вероятности, где a,b- границы интервала распределения.
3)dt(x,d) - плотность вероятности для распределения Стьюдента, где d- число степеней свободы.
Распределением Стьюдента или “t”- распределением называется распределение отношения
где ξ , ξi – независимые, нормально распределенные случайные величины с нулевым математическим ожиданием и единичной дисперсией. Параметр ‘d” называют числом степеней свободы. Распределение Стьюдента широко используется в дисперсионном анализе.
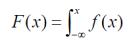
Рахмаев АО РСК-21
4) dchisq(x,d) – плотность распределения χ- квадрат, где х – случайная величина, d- число степеней свободы.
Распределением хиквадрат с “d” степенями свободы называется распределение суммы квадратов “d” независимых случайных величин, каждая из которых подчинена нормальному закону распределения с математическим ожиданием, равным нулю и дисперсией, равной единице. Аналитически это распределение выражается через гамму - функцию. Закон распределения хи – квадрат используется во многих задачах математической статистики.
5)dF(x,d1,d2) – плотность вероятности Фишера, где x, d1, d2, - случайная величина и две степени свободы, соответственно.
Все встроенные функции плотностей вероятностей в Маткаде начинаются с буквы d (distribution)- распределение.
Как известно, функция или интегральный закон распределения F(x) показывает вероятность попадания случайной величины х на отрезок оси абсцисс (-∞, х). и математически записывается как
где f(x) – соответствующая плотность вероятностей.
В Маткаде эти законы строятся с помощью встроенных функций:
pnorm(x,m,σ)- интегральный нормальный закон распределения с математическим ожиданием m и среднеквадратичным отклонением σ;
punif(x,a,b) – интегральный равномерный закон распределения в пределах а и b.
pchisq(x,d) – интегральный закон распределения хи – квадрат с “d” степенями свободы;
pF(x,d1,d2) – интегральный закон распределения Фишера со степенями свободы
“d1”и”d2”.
pt(x,d) – интегральный закон распределения Стьюдента со степенью свободы “d”.

Рахмаев АО РСК-21
Практика Вариант 9
Задача 1. Сгенерировать последовательность случайных чисел R, распределенных по нормальному закону (с использованием функции rnorm). Задайте следующие параметры выборки:
1)объем выборки 100 элементов,
2)математическое ожидание равно N,
3)дисперсия N∙10-1, где N – номер варианта.
Вычислить числовые характеристики, построить гистограмму распределения случайной величины.
Вариант 9
N 9
|
N 10 1 0.949 |
N 10 1 |
Дисперсия, и корень из ней, для вставки в rnorm. |
|
0.9 |
R rnorm(100 N ) |
Получение |
распределения по |
|
|
|
||
mean(R) 8.857 |
нормальному закону. |
||
|
|
|
|
Среднее значение. |
|
|
|
stdev(R) 0.927 |
Среднеквадратичное отклонение. |
||
max(R) 11.892 |
Максимальное число. |
||
min(R) 6.248 |
Минимальное |
число. |
|
|
|||
50
40
30
Gisto gramma j
20
10
0
4 |
6 |
8 |
10 |
12 |
14 |
intj
Гистограмма распределения представлена на рисунке 1.
Задача 2. Рассчитать значения корреляционного момента и коэффициента корреляции по заданным реализациям случайных величин Х, У и Z, W. Проанализировать полученные результаты.
|
103 |
|
3 |
|
12 |
|
144 |
Заданные массивы чисел. |
||||
|
92 |
|
|
2 |
|
|
13 |
|
|
169 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
105 |
|
5 |
|
14 |
|
196 |
|
||||
|
111 |
|
|
9 |
|
|
15 |
|
|
225 |
|
|
|
|
|
|
|
|
|
|
|
||||
X 97 |
|
Y |
0 |
|
Z |
16 |
|
W |
256 |
|
|
|
|
86 |
|
|
1 |
|
|
17 |
|
|
289 |
|
|
|
|
|
|
|
|
|
|
|
||||
120 |
|
6 |
|
18 |
|
324 |
|
|||||
|
89 |
|
|
7 |
|
|
19 |
|
|
361 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
5 |
|
|
20 |
|
|
400 |
|
|
|
cvar(X Y) 16.975 |
cvar(Z W) 213.333 |
corr(X Y) 0.476 |
corr(Z W) 0.998 |
После |
чего |
получаем |
|
корреляционные |
моменты |
и |
|
коэффициенты корреляции.
Проанализировать результаты не представляется возможным, из-за отсутствия математической базы по курсу математической статистике.
Рахмаев АО РСК-21
Задача 3. Построить графики распределения случайной величины на интервале
x:=0..100:
0.1
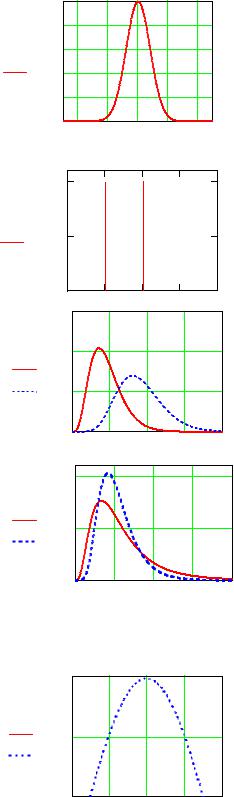
1) нормального закона распределения;
Nor(x) dnorm(x 50 4)
График распределения на рисунке 2.
2) равномерного закона на интервале 10-20;
Ravn(x) dunif(x 10 20)
График на рисунке 3.
3) закона распределения хи – квадрат при числе степеней свободы N, 2N, где N – номер варианта;
d N
d2 2 N
Hi(x) dchisq(x d) Hi2(x) dchisq(x d2)
Графики на рисунке 4.
4) закона z- распределения Фишера (d1=N, d2=N+3; 2 d1=2N, d2=3N+3);
d1 N d2 N 3
0.08
0.06
Nor(x)
0.04 |
|
|
|
|
|
0.02 |
|
|
|
|
|
|
0 |
|
|
|
|
|
30 |
40 |
50 |
60 |
70 |
|
|
|
x |
|
|
|
0.1 |
|
|
|
|
Ravn(x) 0.05 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
|
0.15 |
|
x |
|
|
|
|
|
|
|
|
Hi(x) |
0.1 |
|
|
|
|
|
|
|
|
|
|
Hi2 (x) |
|
|
|
|
|
|
0.05 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
|
|
|
x |
|
|
|
1 |
|
|
|
|
Fish (x) |
|
|
|
|
|
Fish2 (x) 0.5 |
|
|
|
|
|
Fish(x) dF(x d1 d2) |
|
|
|
|
|
|
|
d12 2N |
d22 3N 3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Fish2x( ) dF(x d12 d22) |
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
x |
|
|
||
Графики на рисунке 5. |
|
|
|
|
|
||
|
|
|
|
|
|
||
5) закона распределения Стьюдента |
|
|
|
|
|
|
|
(d=N,d=10N). |
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
d N |
|
|
|
|
|
|
|
Stu(x) dt(x d) |
Stu(x) |
|
|
|
|
|
|
|
0.35 |
|
|
|
|
||
d2 10N |
|
Stu 2(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Stu2(x) dt(x d2) |
|
|
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
Графики на рисунке 6. |
|
1 |
0.5 |
0 |
0.5 |
1 |
|
x
Рахмаев АО РСК-21
Вывод
В общем, и в целом в результате работы получены навыки работы со статистическими функциями MathCAD. Изучены основные математические распределения, и способы их задания в MathCAD. Изучены основные способы статистической оценки множеств значений с помощью функций MathCAD.
