6. Спектральный состав тока в нелинейном элементе при внешнем гармоническом воздействии

Рассмотрим цепь, состоящую из последовательного соединения источника гармонического сигнала , источника постоянного напряжения смещенияи безынерционного нелинейного элемента. Для этого рассмотрим рисунок.

Ток в цепи имеет не синусоидальную форму. Форма тока и напряжения оказывается различными. Причина искажения кривой тока проста: одинаковым приращениям напряжения отвечают неодинаковые приращения тока, т.к. , а дифференциальная крутизна ВАХ на разных участках различна.

Рассмотрим задачу аналитически. Пусть нам известна нелинейная функция . На нелинейный элемент действует напряжение сигнала. Безразмерная величина, тогда- периодическая функция относительно аргументас периодом. Представим ее рядом Фурьес коэффициентами.

Функция четная, поэтому ряд Фурье будет содержать только косинусные составляющие:

.

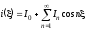Амплитудные коэффициенты гармоник

,

. n=1,2,...

Две последние формулы дают общее решение задачи о спектре тока в нелинейном элементе при гармоническом внешнем воздействии.

.

Т.е. ток, кроме постоянной составляющей , содержит бесконечную последовательность гармоник с амплитудами. Амплитуды гармоник зависят от параметрови, а также от вида аппроксимирующей функции. Рассмотрим каким образом зависит от вида аппроксимирующей функции.

При кусочно-линейной аппроксимации

Подано напряжение .

График тока имеет вид косинусоидальных импульсов с отсечкой. Угол отсечки импульсов тока определяется из равенства .

При степенной аппроксимации

Пусть в окрестности рабочей точки 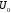ВАХ нелинейного элемента представлена в виде

На вход подается напряжение . Подставляя получаем

Формулы преобразования степеней cos

Получаем соотношения для расчета постоянной составляющей и амплитуд гармоник тока

Постоянная составляющая и амплитуды четных гармоник определяются коэффициентом степенного ряда с четными номерами. Амплитуды нечетных гармоник зависят лишь от нечетных номеров.

Общее выражение

Преобразование спектра входного сигнала в нелинейных цепях является важным явлением. С одной стороны, на нем основана работа целого ряда радиотехнических устройств (модуляторов, детекторов); с другой, из-за не линейности характеристик возникают нежелательные эффекты.

Рассмотрим транзисторный усилитель, нагрузкой которого служит резистор .

Будем полагать, что амплитуда входного сигнала достаточно велика для того, чтобы учитывать не линейность характеристики транзистора. Пусть эта характеристика задается многочленом второй степени

На входе . В коллекторной цепи будем иметь постоянную составляющую тока, а так же токи, отвечающие первой и второй гармоникам частоты сигнала.

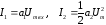
Это гармоники тока, проходя через резистор нагрузки, создают на нем падение напряжения, которое является выходным сигналом. Для того, чтобы количественно оценить степень искажения сигнала на выходе усилителя, вводят величину - коэффициент нелинейных искажений. Эта величина равна отношению среднеквадратического уровня всех высших гармоник тока к амплитуде тока полезного сигнала:

.

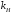В данном случае . Т.к. увеличивается с ростом нелинейных искажений.

Лекция № 4 по курсу

“Теория электрической связи”