4. Прохождение случайных сигналов через линейные цепи с постоянными параметрами

Предположим, что на входе линейной стационарной системы присутствует колебание , представляющее собой некоторую реализацию случайного процесса. Если эта реализация указана заранее, то никакой новой задачи не возникает - к сигналуследует относится как к детерминированной функции. Зная математическую модель системы, например частотный коэффициент передачи, можно найти выходную реакцию.

Однако специфика состоит в том, что полные сведения о входном сигнале недоступны - мы располагаем лишь сведениями об усредненных вероятностных характеристиках случайного процесса .

Цель - исследовать связь между статистическими характеристиками процессов и, которая может быть найдена на основе математической модели системы.

Введем ограничение - будем рассматривать лишь стационарные входные случайные процессы . Математическое ожиданиемгновенных значений реализаций постоянно во времени (), в то время как функция корреляции зависит лишь от величины- абсолютного сдвига между точками на оси времени.

Рассмотрим отдельно взятую реализацию входного сигнала и представим ее в виде интеграла Фурье

где - спектральная плотность.

Выходной сигнал системы будет найден, если известен ее частотный коэффициент передачи

(1)

Предположение о стационарности процесса накладывает условие: среднее значение спектральной плотности.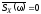

Выполняя статистическое усреднение в обеих частях выражения (1), имеем

(2)

Для того, чтобы вычислить функцию корреляции , необходимо располагать значением выходного сигнала в момент времени.

(3)

Т.к. функция вещественна, поэтому формула (3) не измениться, если в ее правой части перейти к комплексно-сопряженным величинам

(4)

(5)

где ; - спектр мощности стационарного случайного процесса . (Используется фильтрующее свойство дельта-функции).

(6)

Спектр мощности выходного случайного сигнала связан с аналогичным спектром сигнала на входе соотношением

(7)

В прикладных задачах часто приходится иметь дело с односторонними спектрам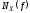и и, которые определены только при положительных частотах,

(8)

поэтому дисперсия выходного сигнала

(9)

Часто приходится рассматривать воздействие на линейные частотно-избирательные цепи широкополосных случайных сигналов, образованных, например, хаотической последовательностью коротких импульсов. В этом случае если эффективная ширина спектра входного случайного процесса значительно превышает ширину полосы пропускания системы, то реальный случайный процесс можно заменить эквивалентным ему белым шумом с односторонним спектром мощности , где- некоторая точка в пределах полосы пропускания цепи.

Тогда формула (9) упростится

(10)

В инженерных расчетах линейную частотно-избирательную цепь, находящуюся под воздействием широкополосного случайного сигнала, удобно характеризовать шумовой полосой пропускания . Она определяется как полоса пропускания идеального полосового фильтра с вещественным коэффициентом передачи, равным максимуму модуля коэффициента передачи реальной цепи. При возбуждении идеальной и реальной систем белым шумом со спектром мощностидисперсии шумовых сигналов на выходах обеих цепей должны совпадать

(11)

Следовательно

(12)

Например, для интегрирующей RC-цепи

;

Следовательно

При этом .

Если входной случайный процесс нормален (гауссов характер законов распределения), то случайный процесс на выходе будет обладать этим свойством независимо от динамических свойств линейной системы.

На основании формулы Дюамеля мгновенное значение отклика

есть результат суммирования предшествующих значений входного сигнала , умноженных на сдвинутую импульсную характеристику цепи.