4. Теорема кодирования для сигнала с помехами
Пропускная способность канала характеризует потенциальные возможности передачи информации. Они раскрываются в фундаментальной теореме К. Шеннона. Применительно к дискретному источнику она формулируется так:
если производительность источника сообщений Н(A) меньше пропускной способности канала С:
, (17)
то существует способ кодирования (преобразования сообщения в сигнал на входе) и декодирования (преобразования сигнала в сообщение на выходе канала), при котором вероятность ошибочного декодирования и ненадёжность Н(А|Â) могут быть сколь угодно малы. Если же H’(A) > C, то таких способов не существует.
А
- ансамбль дискретных сообщений; В -
ансамбль дискретных сигналов.
если
А В обратимо. Если необратимо
и
разность
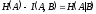можно назватьпотерей
информации
при преобразовании А В. Её называют
также ненадёжностью. Т.о., согласно
теореме Шеннона конечная величина С -
это предельное значение скорости
безошибочной передачи информации по
каналу. Эта теорема, к сожалению, не
конструктивна, т.е. она не указывает
конкретного способа кодирования,
существование которого доказывает. Тем
не менее, значение теоремы трудно
переоценить, ибо она в корне изменила
воззрения на принципиальные возможности
техники связи. До Шеннона считалось,
что в канале с шумами можно обеспечить
сколь угодно малую вероятность ошибки
только при неограниченном уменьшении
скорости передачи информации. Таков,
скажем, путь повышения верности связи
за счёт повторения символов в канале
без памяти.
Сообщения
источника а1
= 0 и а2
= 1 можно передать по двоичному симметричному
каналу с вероятностью ошибок p
< 0,5
двумя кодовыми комбинациями соответственно
n
единиц и n
нулей:
.
Если в месте приёма регистрировать “1”
или “0” по большинству этих знаков в
кодовой комбинации (мажоритарное
декодирование), то ясно, что ошибка
произойдёт при условии, если в кодовой
комбинации не верно будет принятоn/2
или более символов.
Согласно
закону больших чисел вероятность
уплотнения числа ошибок m
в кодовой комбинации длины n
от
их математического ожидания 0 при n
:
(12)
при сколь угодно малом положительном . Т.к. np < n/2 код обеспечит при n безошибочный приём, однако одновременно при этом и скорость передачи информации по каналу 0, тогда как согласно теореме Шеннона существуют коды, обеспечивающие сколь угодно малую вероятность ошибки при конечной скорости передачи информации.