3.4.8. Распределение Стьюдента

Это распределение безразмерной СВ t, которую называют дробь Стьюдента. Она образована отношением двух независимых СВ: уклонением от математического ожидания к нормированному СКО : , (3.39)

где x - нормально распределенная СВ с математическим ожиданием M{x} и неизвестной дисперсией s²,

s² случайная величина, подчиняющаяся распределению ² с r степенями свободы.

Плотность распределения этой дроби предсказал Стьюдент (английский статистик Госсет (1876-1937)) и доказал Р.А.Фишер.

Плотность распределения Стьюдента определяется выражением (рис.3.5д) , (3.40) где .

Числовые характеристики распределения таковы: математическое ожидание M{t}=0 при r>1; дисперсия s² =r/(r-2) при r>2; асимметрия А=0 при r>3; эксцесс E=3(r-2)/(r-4)-3=6/(r-4), при r>4.

Это симметричное распределение с одним параметром r. При малом числе степеней свободы эксцесс положителен, т. е. кривая распределения имеет пик и широкое основание. С увеличением степеней свободы r распределение стремится к нормальному. Например, при r=29 E=0.24. Распределение Стьюдента применяют для установления предела уклонений СВ от среднего при небольшом объеме наблюдений.

Применительно к наблюдениям дробь Стьюдента есть ни что иное, как уклонение наблюдения, нормированное значением стандарта, вычисленного по этим же самым наблюдениям.

(О Стьюденте. В начале 1900х лет один из директоров пивоваренного завода в Дублине (Arthur Guinnes) прочитал книгу по теории вероятностей и решил из этого делать деньги. С этой целью он послал младшего клерка пивоварни Уильяма Госсета на учебу к Карлу Пирсону в Лондон в Университетский колледж. После учебы тот самостоятельно стал работать в этой области на пивоваренном заводе. Одни его разработки оказались очень ценными для пивоварения, другие – общетеоретического плана. Компания не возражала против публикации Госсетом его трудов, но, чтобы конкуренты не узнали об использовании статистики в пивоварении, предлагала публиковать так, чтобы конкуренты не догадались, что автор, служащий пивоварни. В результате в журнале Biometrika был опубликован ряд первоклассных статей под псевдонимом Student.)

3.4.9. F-распределение Фишера-Снедекора

Распределение впервые нашел Р.А. Фишер, изучил распределение Д.У. Снедекор. Это распределение отношения двух СВ Q₁ и Q₂ (см.(3.38)): . (3.41) Обе СВ следуют распределению ² с r₁ и r₂ степенями свободы соответственно. Функция плотности вероятности этого распределения (см. рис.3.5е): , (3.42) где , (r)- гамма-функция. Все числовые характеристики этого распределения определяются числами степеней свободы. Первые две такие: математическое ожидание ;

дисперсия . (3.43)

Распределение применяется для определения интервальных характеристик, для сравнения точности измерений, для оценки существенности влияния фактора (систематических ошибок) на результаты наблюдений, при подборе полиномов, аппроксимирующих кривую.

________________________ _______________________

а) биномиальное б) равномерное

________________________ _____________________

в) антимодальное г) хи-квадрат

_________________________ ____________________

д) Стьюдента е) Фишера

Рис.3.5. Функции вероятности (плотности вероятности) распределений

DIXI

APPENDIX

Учет асимметрии и эксцесса. Функция Шарлье при асимметрии А=0 и эксцессе Е=0 распределение Шарлье совпадает с нормальным, иначе

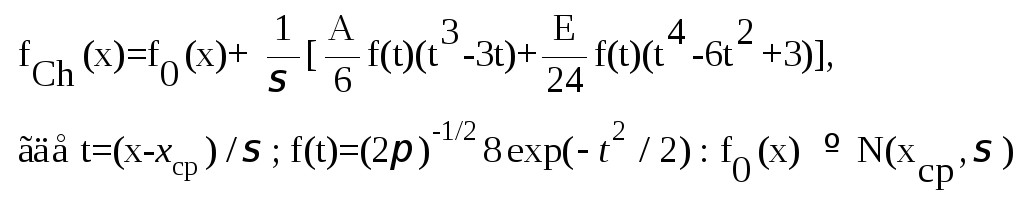, т.е. второе слагаемое есть поправки за А и за Е.

Распределение Гудрича Скорость ветра у земли

Скорость ветра в свободной атмосфере – распределения Релея , где-функция Бесселя нулевого порядка, - модуль результирующего ветра .

Распределение элементов, ограниченных с обеих сторон (количество облаков, направление ветра) – распределение есть функция Пирсона первого порядка

Трехпараметрическая кривая гамма-распределения Крицкого-Менкеля ,показатель степени b находится по методу моментов

Сл. тема интервальные оценки. (из главы GО4)Требование ГОСТ Метод доверительных интервалов (1996 рассказана здесь же)

4.2.3.4. Метод доверительных интервалов. Метод разработан Р. А. Фишером и Ю.Нейманом (ссылка?).

Наглядно суть метода такова. На графике функции плотности вероятности на ее средней части выделяют площадь, составляющую вероятность , оставляя справа и слева обычно равные площадки (1-β)/2. Значения абсцисс, ограничивающих эту площадь, служат границами интервала на оси Х. Вероятность , а также интервал называют доверительными.

Исходя из объема выборки или из других соображений, например, требований производства, определяют доверительную вероятность , с которой интервал накрывает оцениваемую характеристику. Наблюденные значения, не попавшие в интервал, считаются относящимися к другой выборке (например, грубые измерения). Эта вероятность  не может быть маленькой, ибо тогда интервал будет коротким, и некоторые правильные наблюдения не попадут в него. Получим слишком строгий отбор. Но! Вероятность не может быть очень большой, ибо тогда ошибочные наблюдения войдут в доверительный интервал. Интервальная оценка будет ненадежной. Подбирают оптимальное значение , исходя из практической задачи. Обоснование интервала и доверительной вероятности рассмотрим позднее. Обычно принимают =0.7 - 0.99.

Зная теоретическое распределение этой характеристики и объем выборки, находят граничные значения доверительного интервала. Или же, задав доверительный интервал, находят объем выборки -

Рассмотрим доверительные интервалы оценок выборки.

4.2.3.4.1. Доверительный интервал отдельного наблюдения. Вначале по формулам выборочного среднего (4.6) и дисперсии генеральной совокупности (4.1) вычисляют оценки . Далее принимая во внимание, что центрированнаяx_ср и нормированная S случайная величина , (4.26) следует распределению Стьюдента S(t,r) (t-распределению), определяют граничные значения t_.

Распределение Стьюдента при числе степеней свободы (объеме выборки) порядка 30 практически близко к нормальному. Поэтому при большом объеме выборки пользуются нормальным распределением.

1. При r<30 прибегают к t-распределению Стьюдента. Для этого по доверительной вероятности  и числу степеней свободы r=n-1, вычисляем граничное значение интервала t_r . Так как t- распределение симметрично, то левое граничное значение t_r будет отличаться только знаком. Подставляя найденные значения в левую часть равенства (4.26), а в правую -вычисленные значения x_ср и S, вычисляем правую и левую границы значений величины Х: x_пр и x_лев :

x_пр = x_ср + t_rS x_лев = x_ср - t_rS. (4.27)

В результате получаем, что математическое ожидание ₁ СВ x (но не xср!) с вероятностью  лежит на интервале x_ср - t_rS<₁< x_ср + t_rS (4.28)

Предупреждение. При n<10 распределение Стьюдента не дает надежной оценки.

2. При r>30 используем нормальное распределение. Выбираем значение t_ по доверительной вероятности . Число r не учитываем. Далее поступаем согласно выражениям (4.27) и (4.28).

3. При известной заранее оценке стандарта S (заданной точности прибора, точности измерений), т.е. при отсутствии ошибки оценки стандарта, вызванной малым объемом выборки, также используют нормальное распределение для определения доверительного интервала.

4.2.3.4.2. Доверительный интервал дисперсии и стандарта отдельного наблюдения. Будем полагать, что в предыдущем пункте оценки x_ср и S² вычислены. Покажем, что при x N(₁,²), оценка S² следует распределению ². Для этого перейдем к нормированной стандартом и центрированной СВ t=(x-₁)/. Она следует нормальному распределению с параметрами (0,1). Поэтому сумма ее квадратов по определению следует ² -распределению: . Отсюда (4.29). С другой стороны из (4.1) получаем. Подставляя в (4.29) вместо суммы квадратов уклонений от истинного центра оценку этой суммы из выборки, мы получаем оценку дисперсии (²) как функцию от переменной ², где коэффициент для данной выборки постоянен: . (4.30). Здесь доверительный интервал находим по самой оценке S², коя всегда находится внутри интервала.

Другая задача: найти доверительный интервал по априорной оценке, с целью отбраковки некоторой выборки. Рассматриваем серию выборок при постоянной дисперсии ²: Например, несколько человек измеряли один и тот же объект на одном и том же приборе, обеспечивающем точность ² . Находим оценку S² этой дисперсии как функцию ² и объема выборки n: (4.31). Здесь доверительный интервал находим по априорной оценке σ^{2 .} Дисперсия у кого-то из измеряющих может оказаться вне интервала.

Значение переменной ² зависит от числа степеней свободы r и доверительной вероятности . Величина ² есть теоретическое значение степеней свободы, т.е. положительная величина, что следует из определения: «сумма квадратов...». Поэтому вся функция плотности вероятности распределения ² лежит в области положительных значений. Для малых r распределение ² асимметрично. Поэтому при малом данном r мы должны найти по доверительной вероятности  левое и правое граничное значение ² (минимально и максимальное число степеней свободы, так как функция ² непрерывна, то это число дробное).

Вся площадь под кривой функции плотности вероятности ² равна единице. Мы вырезаем в ней область доверительных значений  так, чтобы слева и справа от этой единичной площади отсекались равные по площади критические области p=(1-)/2. Тогда площадь критической области будет ограничена слева вертикальной прямой с абсциссой

, а справа - вертикальной прямой . (4.32)

Пользуясь значениям p_лев и p_пр , из распределения ² для данного r=(n-1) находим значения _лев² и _пр² (минимальное и максимальное числа степеней свободы). С их помощью по (4.30) вычисляем границы доверительного интервала дисперсии. Толкование смысла интервала зависит от надежности дисперсии.

1. Оценка дисперсии найдена из выборки. (Значение дисперсии не известно априори). Подставив значения _лев² и _пр² в (4.30), получаем границы доверительного интервала, накрывающего искомый параметр ² с вероятностью : (4.33)

Интервал показывает пределы (для нас главное правый) возможной дисперсии при данном числе наблюдений: если правая граница далека, то оценка весьма условна.

2. Значение дисперсии известно априори. Оцениваем качество наблюдений. Подставив значения _лев² и _пр² в (4.31), получаем границы доверительного интервала, накрывающего искомую оценку S² с вероятностью : . (4.34)

Если найденная из выборки оценка S² вне расчетного интервала, то либо точность наблюдений не соответствует априорной (низка или высока), либо на наблюдения повлиял некий фактор.

Определение доверительного интервала оценки стандарта (СКО). Для этой цели достаточно извлечь положительный квадратный корень из неравенств (4.33) для искомого параметра σ: , (4.35) или из (4.34) для проверки оценки СКО: . (4.36)

4.2.3.4.3. Доверительный интервал оценки асимметрии. Нулевая гипотеза: асимметрия равна нулю. Если вычисленное значение асимметрии выходит за пределы доверительного интервала, то оно считается существенным, позволяющим считать с вероятностью , что распределение выборки асимметрично, знак указывает направление шлейфа (хвоста) выборки. Если же оценка лежит внутри доверительного интервала, то асимметрия считается несущественной, практически нулевой.

Для нахождения доверительного интервала вычисляется дисперсия асимметрии: . (4.37)

Задается доверительная вероятность  (можно t, так для нормального распределения t_=2 имеем =0.9, а для t_=3 - =0.997). Доверительный интервал будет . (4.38)

4.2.3.4.4. Доверительный интервал оценки эксцесса. Исходным предположением об эксцессе является его равенство нулю. Если оценка эксцесса лежит внутри доверительного интервала, то он считается несущественным, практически нулевым. Если найденная оценка эксцесса выходит за пределы доверительного интервала, то это позволяет считать с доверительной вероятностью , наличие эксцесса, положительного или отрицательного. Для нахождения доверительного интервала вычисляется дисперсия эксцесса: . (4.39)

Задается доверительная вероятность  или непосредственно t для нормального распределения, аналогично асимметрии. Доверительный интервал будет: . (4.40)

Примечание. Встречаются другие варианты формул вычисления S_А и S_Е, но при их упрощении они преобразуются к вышеприведенному виду.