Лекции / Лекции (2 семестр) / VAR-SOST

Лекция 6. Метод переменных состояния.

К числу важнейших параметров, характеризующих свойства инвариантных относительно времени схем, относятся:

1. Переходная характеристика, необходимая при рассмотрении воздействия на схему сигналов произвольной формы;

2. МYП позволяет рассчитывать линейный и нелинейные схемы на постоянном и переменном токе, получил широкое распространение при расчете на ЭВМ. Однако, для указанных целей неудобен, поскольку система управлений по МУП представляет собой систему интегро-дифференциальных уравнений. Можно перейти в область изображений и получить требуемую передаточную функцию в виде дробно-рациональной функции:

H(p)=N(p)/D(p).

Для определения нулей и полюсов необходимо решать уравнения N(p)=0 и D(p)=0. Чтобы найти переходную характеристику, следует умножить D(p) на p. Далее необходимо разложить дробно-рациональную функцию и выполнить обратное преобразование Лапласа для каждого слагаемого.

Данный подход в применении к большим схемам имеет следующие недостатки:

1. Чтобы получить коэффициенты полиномов N(p) и D(p), приходиться вычислять ряд определителей, элементы которых содержат p. Такой процесс решения является нетривиальной задачей.

2. Вычисление корней уравнений N(p)=0 и D(p)=0 производиться по различным итерационным процедурам, при которых возможны значительные численные погрешности.

3. Другим источником погрешностей является процедура разложения дробно-рациональной функции в том случае, когда несколько полюсов совпадают или имеют близкие значения.

4. Вычисление производной n-го порядка при выполнении обратного преобразования Лапласа, как правило, производится через производную (n-1)-го порядка - еще один источник погрешности.

Можно ли повысить эффективность МУП? Да! Однако, это возможно лишь в том случае, когда для вычисления переходной характеристики используются соответствующие дискретные модели схем, методы численного интегрирования и методы разложения матриц. При решении задачи определения нулей и полюсов приходится прибегать к искусственным методам (например, в качестве модели катушки индуктивности применяется пара гиратор-емкость).

Все же остается ряд задач (импульсные системы), при решении которых с помощью МП возникают различные трудности.

Основная идея МЕТОДА ПЕРЕМЕННЫХ СОСТОЯНИЯ состоит в записи уравнений во временной области дифференциальных уравнений первого порядка.

Линейную инвариантную относительно времени схему представляют двумя уравнениями.

[]= [A] * [x] + [B] * [u]

[y] = [C] * [x] + [D] * []

[u] - входной вектор, описывающий m независимых источников, размерности [m x 1];

[y] - вектор, описывающий i выходов (напряжений и/или токов), размерности [i x 1];

[x] - вектор, содержащий n независимых вспомогательных переменных, размерности[n x 1];

[A], [B], [C], [D] - матрицы с постоянными коэффициентами соответствующего размера, причем [A] - всегда квадратная матрица порядка n.

(1) - система n дифференциальных уравнений первого порядка (в общем случае взаимосвязанных), называемая УРАВНЕНИЕМ ПЕРЕМЕННЫХ СОСТОЯНИЯ в нормальной форме. Вспомогательные переменные х, х...х - ПЕРЕМЕННЫЕ СОСТОЯНИЯ, а [x] - вектор переменных состояния.

(2) - выходное уравнение.

Преимущества:

1. Решение таких систем широко известно в математике как в численном, так и в аналитическом виде.

2. Уравнения легко решаются на ЭВМ.

3. Как правило, число уравнений в системе (1) оказывается меньше, чем число уравнений, составленных МУП.

4. Метод может быть обобщен для решения нелинейных систем.

СТЕПЕНЬ СЛОЖНОСТИ И НАЧАЛЬНЫЕ УСЛОВИЯ.

Для любой схемы с сосредоточенными параметрами справедливы 1 и 2 законы Киргофа, а также существует соотношение между током и напряжением для каждого из элементов. Если с их помощью удается получить систему линейно независимых дифференциальных уравнений первого порядка.

[]= [ f ( [x], t) ]

где [x] - набор из n независимых вспомогательных переменных, то говорят, что для данной схемы существует УРАВНЕНИЕ ПЕРЕМЕННЫХ СОСТОЯНИЯ В НОРМАЛЬНОЙ ФОРМЕ.

n - определяет СТЕПЕНЬ СЛОЖНОСТИ схемы.

Состояние схемы определяется минимальным набором элементов.

Набор переменных называется ПЕРЕМЕННЫМ СОСТОЯНИЯ схемы, если для него выполняются условия :

1. Состояние схемы в любой момент времени t и входные действия при t однозначно определяют состояние схемы при любом t> t.

2. переменные состояния совместно с входными воздействиями однозначно определяют значения любых переменных в схеме в любой момент времени.

Общее решение (1) должно содержать n независимых постоянных интегрирования, которые определяются с помощью n НАЧАЛЬНЫХ УСЛОВИЙ. Обычно в качестве начальных условий берутся значения переменных в момент времени t=0. При этом степень сложности схемы равна числу НЕЗАВИСИМЫХ НАЧАЛЬНЫХ УСЛОВИЙ, которые обязательно задаются в виде электрических величин, обеспечивающих получение полного решения [ x (t) ] и [ y (t) ].

Определяющими величинами для линейных схем ( на основании начальных значений которых можно получить решение для всех токов и напряжений в схеме ) являются напряжения (заряды) на конденсаторах и токи (потокосцепления) в катушках индуктивности.

Напряжения на катушках индуктивности и токи через конденсаторы не всегда обеспечивают требуемый результат. Например, при известном токе через конденсатор для расчет напряжения на нем необходимо знать не начальный ток, а начальное напряжение.

Поэтому, помимо указанных условий, переменные состояния выбирают таким образом, чтобы их начальные условия позволяли бы решать систему (1).

ОПРЕДЕЛЕНИЕ ПОРЯДКА СИСТЕМЫ УРАВНЕНИЙ ПО МПС.

Число уравнений в системе равно числу независимых напряжений на емкостях и токов, протекающих через индуктивности.

Зависимость между напряжениями и токами может возникнуть в следующих случаях :

1. СЕ - контур, образованный емкостями и независимыми источниками ЭДС.

2. LJ - сечения, образованные индуктивностями и независимыми источниками тока.

СТЕПЕНЬ СЛОЖНОСТИ RLC цепей : n = , где

b - полное число конденсаторов и индуктивностей.

n - число независимых СЕ контуров.

n _L - число независимых LJ сечений.

Две задачи : формирование уравнений в пространстве состояний и их решение.

ФОРМИРОВАНИЕ УРАВНЕНИЙ В ПРОСТРАНСТВЕ УРАВНЕНИЙ.

Подобно уравнениям, составленным по МКТ, МУП и т.д., уравнения состояния представляет из себя преобразованные к определенному виду уравнения цепи.

Задача состоит в том, чтобы получить уравнения (1) и (2). При получении (1) требуется выразить производные от переменных состояния через сами переменные состояния. Поскольку производные по времени от переменных состояния ( токи через индуктивности и напряжения на конденсаторах ) можно связать с напряжениями на индуктивностях и токами через конденсатор, задача состоит в определении связи между токами через конденсаторы и напряжениями на них, а также на индуктивностях и их токами.

I. Наиболее общий подход к анализу цепей основан на законах Киргофа. Уравнения в пространстве состояний могут быть получены путем преобразований уравнений, записанных по законам Киргофа. Рассмотрим такой подход к получению уравнений на следующем примере :

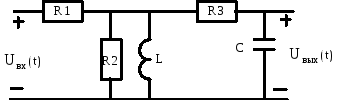
R = 1K; R = 3K; R = 2K; L = 50 мГн; C = 0.01 мкФ

Запишем соотношения между токами и напряжением на реактивных элементах :

; (4)

Выходное уравнение :

Запишем первый закон Киргофа для узла :

(5)

Причем : / R; (6)

Подставим (4) в (5) и (6) :

(7)

(8)

(7) и (8) приводим к форме Коши :

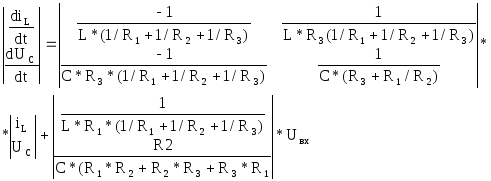
Выходное уравнение : U (9)

Из (9) и (10) можно записать матричные коэффициенты уравнения в пространстве состояний.

[x] = [u] = [U]; [y] = [U];

[A] = ; [C] = [0 1]; [D] = [0];

[B] =

Недостатки :

1. Сложно для схем второго порядка.

2. Наличие взаимных индуктивностей и зависимых источников усложнит процесс получения.

3. Плохо алгоритмизуем, практически невозможно переложить на ЭВМ. При ручных расчетах высока вероятность ошибок.

II. Сведение задачи к расчету цепи по постоянному току.

Рассмотрим общий случай для схемы инвариантной относительно времени (m- число входных переменных; n - число переменных состояния; j - число входных переменных ).

Перепишем исходные уравнения :

[]= [A] * [x] + [B] * [x] (1)

[y] = [C] * [x] + [D] * [u] + ( [D] * [] + ...) (2)

Если в выходном уравнении отсутствуют [ [ D] * [ (t) ] + ...], такая система называется ПРАВИЛЬНОЙ. В дальнейшем будем рассматривать исключительно правильные системы.

В качестве переменных состояния выбраны напряжения на конденсаторах и токи через индуктивности :

В более компактном виде можно записать:

[P] = [Q] * [ z ] (11)

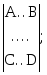где [P] = [Q] = [z] =;

Размерности : [P] - вектор [n+j];

[z] - вектор [m+n];

[Q] - вектор [n+j]; строк и [m+n] столбцов.

Отметим, что матрицы и векторы (11) получены из (1) и (2) простой перенумерацией элементов. Значения элементов остаются неизменными.

Очевидно, что элементы [Q] могут быть определены следующим образом:

q(i,l) = p(i), если z(k) = k=1,..(n+m)

Это означает, что l-й столбец [Q] равен вектору [P], полученному при решении цепи, когда k-й элемент [z] единичным источником , а все остальные члены [z] приравняны к нулю. Данное решение может быть получено для эквивалентной схемы, составленной по следующим правилам:

1. Конденсаторы заменяются короткими замыканиями.

2. Индуктивности заменяются разрывами ветви.

3. Источники ЭДС заменяются короткими замыканиями.

4. Источники тока заменяются разрывами ветви.

5. Выбранный (k-й) элемент заменяется единичным источником (1В- для источников ЭДС и конденсаторов и 1А - для источников тока и индуктивностей).

6. Повторение процедуры до тех пор , когда k не превысит (n+m).

7. В результате вычислений получим токи через все конденсаторы и направление на все индуктивности. Формируем вектор [P’].

8. Переходим от токов через конденсаторы и напряжений на индуктивностях к исходным переменным состояния.

Для выполнения п.8 рассмотрим связь между напряжениями и токами на реактивных элементах.

Производные по времени от [x] можно связать токами через конденсатор и напряжениями на индуктивности.

k = 1, ... K

Или в матричной форме: [I] = [C] * (12)

[I] - вектор токов через конденсаторы размерностью [K x 1];

[U] - вектор напряжений на конденсаторах размерностью [K x 1];

[C] - [ K x K ] диагональная матрица, чьи элементы определяются соотношением C( i , j ) = ( i , j ) * C ( j )

Переходя к производным:

(13)

[S] = [C] -диагональная матрица с положительными членами.

Пусть схема содержит P индуктивностей, которые могут быть связными. Напряжение на j-й индуктивности представляет собой сумму, один из членов которой обусловлен протеканием тока через j-й индуктивность, другие - токами через индуктивности , связанными с j-й:

U (14)

В матричной форме: [U] = [L] * (15)

[ U ] - вектор напряжений на индуктивностях размерностью [P x 1];

[ I ] - вектор токов через индуктивности размерностью [P x 1];

[L] - [P x P ] матрица, диагональные элементы которой являются собственными, а недиагональные члены - взаимными индуктивностями. Члены [L] могут иметь как “+” , так и “-” знаки.

Решаем (15) относительно производных:

(16)

Объединяя (13) и (16) , получим:

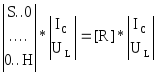[]= (17)

[R] - квадратная матрица размерностью [(P+K) x (P+K)]. Матрица имеет более простой вид, если вектор [x] упорядочен, т.е. конденсаторы и индуктивности объединены в группы. В отсутствии взаимных индуктивностей в матрица [H], а следовательно и [R], представляет собой диагональные матрицы. Если вектор [x] упорядочен, то на главной диагонали [H] вначале будут находиться члены, обратные емкостям, далее - члены, обратные индуктивностям. Возможен и обратный порядок следования членов. При наличии взаимных индуктивностей, матрицу [H] необходимо вычислять обращением матрицы [L]. В данном случае упорядовачивание вектора [x] значительно упростит вид [H].

Используя соотношение (17), можно осуществить переход от вектора к вектору [P’] к вектору [P]. При этом следует отметить , что переход необходимо выполнить не для полного вектора [P], а для его первых n(n=P+K) членов .

Тогда :

[P]=[R]*[P’ ] (18)

Очевидно, что при выполнении описанной процедуры следует оперировать с численными значениями элементов матриц.

Проиллюстрируем алгоритм на примере схемы, рассмотренной ранее.

Вектор переменных состояния как и ранее: [x] = [i U

u=U; y=U;

формируем вектор [P] =[

[P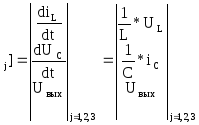

Для получения первого столбца [Q] воспользуемся z(k)=(k , j) при j=1

Для определения вектора [P1] эквивалентная схема будет иметь следующий вид:

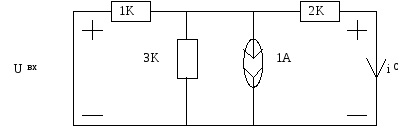
U= -545 B;

i

Выходное напряжение U=0

Следовательно:

[P]=

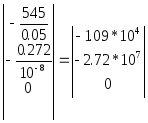
Аналогично для j=2, 3 ;

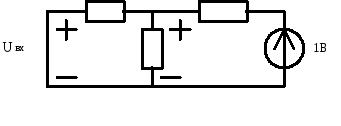
[P] =

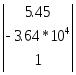
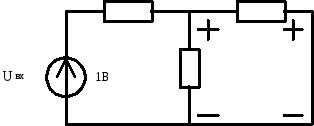
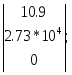
[P] =

[Q] =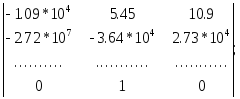

Метод применим для схем, содержащие зависимые источники. Никаких преобразований зависимых источников не производиться.

Недостатки:

1. При построении программ на основании данного алгоритма конденсатор заменяется на малое сопротивление (0.01 Oм), а индуктивность - на большое (10 Ом). Источник погрешности.

2. Дополнительный источник численной погрешности - инвертирование матриц [C] и [L].

Алгоритмы формирования уравнений по МПС, обеспечивающие меньшие численные погрешности, основаны но формировании дерева при правильном или неправильном размещении и используют, как правило, матрицу инциденций.( Л.О. Чуа, Пен-Мин-Лин. Машинный анализ электронных схем. -М.: Энергия, 1980).

III. Формирование уравнения в пространстве состояний на основании дифференциального уравнения n-го порядка.

[]=[A] * [x] + [B] * [x] Метод Бэка.

Пусть имеем:

Введем обозначения:

x = x;

Тогда исходное уравнение может быть представлено в виде:

или в матричной форме:

[] = [A] * [x] + [B] * [u]

РЕШЕНИЕ УРАВНЕНИЙ ПЕРЕМЕННЫХ СОСТОЯНИЯ ВО ВРЕМЕННОЙ ОБЛАСТИ.

Пусть задана схема, описываемая уравнениями (1) и (2):

[] = [A] * [x] + [B] * [u];

[y]= [C] * [x] + [D] * [u];

начальными условиями [x(t)] и входным вектором [u(t)] при t>= t. Требуется найти выходной вектор [y(t)] при t>= t.

Решение выходного уравнения при известных [u(t)] и [x(t)] не вызывает трудностей. Поэтому основное внимание будет уделено решению уравнения (1), которое представляет собой линейное матричное дифференциальное уравнение с постоянными коэффициентами.

Вначале рассмотрим решение скалярного уравнения первого порядка. После получения решения методом вариации постоянных и рассмотрение свойств матричных функций, результат будет обобщен на матричное дифференциальное уравнение.

= a * x + b * u

Задано начальное условие [x(t)]. Требуется определить зависимость x(t) при t>= t. Для отыскания решение воспользуемся методом вариации постоянных.

Вначале рассмотрим тривиальный случай, когда u (t) =0, т.е. уравнение (19) - однородное. Общее решение в этом случае имеет вид:

x(t) = e * K

где К - произвольная постоянная.

ПриU(t) 0, решение (19) будем искать, полагая, что К является функцией от t:

x(t) =e * K(t) (20)

Поскольку предполагается, что (20) является решением (19), подставим его в исходное уравнение и после дифференцирования получим:

a * e * K(t) + e * K(t) = a * e * K(t) +b * u(t); (21)

Следовательно :

(t) = e * b * u(t) = e* b * u(t) (22)

Интегрируя обе части (22) в пределах от t= t до t, получим:

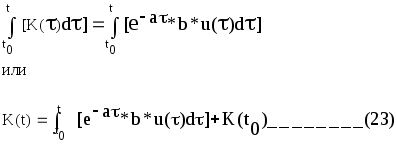
Из уравнений (20) и (23) получаем:

x(t) = 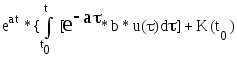} (24)

Для определения положим из уравнения (20) t= t:

x(t) =* K (t)

или K(t) = * x(t)

Таким образом, решение уравнения (19) имеет вид:

x(t) = e* x(t) + [e* b * u()d] (25)

x(t) в момент времени t= t является начальным условием и представляет собой “предысторию” схемы от -до t.

Получение уравнение определяет поведение схемы в диапазоне времени

t<= t < с учетом информации о входном сигнале.

Выходная переменная будет определятся из уравнения:

y(t) = c * x(t) + d * u(t) = c * e * x(t) +

реакция схемы при нулевом

входном воздействии

+ c * 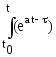* b * u() d ] + d * u(t)

реакция схемы при нулевых начальных условиях

Решение линейного уравнения a * x = k можно представить в форме

x = a* k. Аналогично, решение системы уравнений [A] * [x] = [k] можно представить в форме [x] = * [k]. Решение в обоих случаях имеют одинаковый вид, за исключением того. что во втором случае скалярные величины заменяются на матричные.

При операциях с матрицами следует помнить, что матричное умножение не является коммутативным. Кроме того, непонятно значение и свойства матричной экспоненциальной функции. Поэтому, прежде чем перейти к обобщению решения, полученного для скалярного уравнения, на матричное уравнение, необходимо определить ФУНДАМЕНТАЛЬНУЮ или ПЕРЕХОДНУЮ матрицу состояния системы:

e= [I] + [A] * t +

Можно показать, что ряд сходится при всех значениях t . Из разложения в ряд Тейлора следует, что e представляет собой квадратную матрицу размерности [n x n] , элементы которой являются функцией времени.