Лекции / Лекции (2 семестр) / 3

Лекция 7. СИНТЕЗ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ.

Задача синтеза: Определить структуру и параметры электрической цепи при заданных возмущении и реакции , т.е. требуется построить схему с заданными частотными характеристиками.

1. Аппроксимация полиномами операторных выражений для возмущения и реакции;

2. Реализация (что и будем рассматривать далее);

3. Оптимизация.

Пусть после первого этапа получена передаточная характеристика цепи F(p) (возможно Z(p) или Y(p) ):

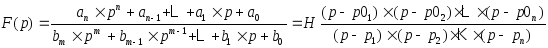
Значения p=¥ , при которых F(p)=¥ называются полюсами функции, p=p0:

F(p)=0 - нулями.

РЕАЛИЗУЕМОСТЬ ОБОБЩЕННЫХ ВХОДНЫХ ФУНКЦИИ.

Свойства входных функций цепи:

1. Все нули и полюса располагаются в левой -полуплоскости или на мнимой оси, причем на мнимой оси не может быть нулей и полюсов кратности >1,

т.е. они будут простыми.

2. Степени полиномов числителя и знаменателя могут различаться не более, чем на 1. В противном случае будет иметь кратный ноль или полюс в бесконечности.

3. Коэффициенты полиномов числителя и знаменателя являются положительными числами.

Для каждой пары комплексно-сопряженных корней:

Т.е. при отрицательных действительных частях имеем положительные коэффициенты. Полиномы с положительными коэффициентами называются полиномами Гурвица.

4. Y(p) и Z(p) являются положительными вещественными функциями

(Re(f)³0) при Re(p) = Re (s+j´w) = s ³ 0 поскольку эти коэффициенты

образуются различным сочетанием R , L , C элементов.

5. При наличии активного сопротивления в какой-либо из ветвей цепи

, в общем случае

СИНТЕЗ РЕАКТИВНЫХ ДВУХПОЛЮСНИКОВ.

В этом случае нули и полюса функции простые и лежат на мнимой оси. Признаком того, что двухполюсник может быть реализован только L и C элементами является то, что полином числителя содержит слагаемые только четных степеней , а знаменателя нечетных (или наоборот).

Существуют два основных подхода к синтезу линейных цепей.

1. Метод Фостера предполагает разложение функции на простые дроби с последующей схемной реализацией.

Запишем разложение исходной дробно-рациональной функции:

(*)

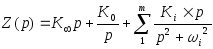K_¥ - вычет функции в полюсе p = ¥ =

K₀ - вычет функции в полюсе p = 0 =

K_i - вычет функции в полюсе p = p_i = j´w =

Схемные реализации:

L₁ L_n

L_¥ C₀

... Z_L = p´L Þ K_¥ = L_¥

C₁ C_n

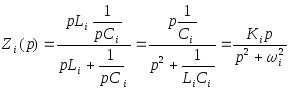
Если же задается функция Y(p) с теми же свойствами:

схемная реализация имеет вид:

. . .

L₁ L_m

C_¥ L₀

C₁ C_m

. . .

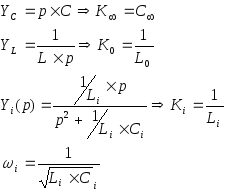
При синтезе реактивных двухполюсников могут встретиться следующие частные случаи:

1. Степень полинома числителя A(p) на 1 выше степени полинома знаменателя B(p) знаменатель содержит нулевой корень.

В этом случае в разложении (*) первые два слагаемые имеет конечную

величину:

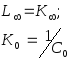
Расположению нулей и полюсов на оси частом соответствует:

Ось частот с расположенными на ней нулями и полюсами называется

ХАРАКТЕРИСТИЧЕСКОЙ СТРОКОЙ.

В начале координат имеется полюс обусловленный емкостью С₀ ,

а в ¥ p_¥ = ¥ , обусловленный наличием индуктивности L_¥ ,

что соответствует схеме:

L_¥ C₀

... для Z(p)

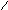. . . для Y(p)

. . .

X_ВХ П

0

. . . w

П

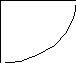
2. Степень полинома числителя А(р) на 1 выше степени полинома знаменателя B(р) ; знаменатель не содержит нулевого корня.

Второе слагаемое в разложении ( * ) отсутствует:

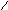
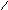
... для Z(p)

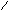
. . . для Y(p)

. . .

X_ВХ

. . . w

3. Степень полинома А(р) не превышает степени полинома В(р); знаменатель содержит нулевой корень.

. Имеется полюс p_¥ = 0, обусловленный С₀

... для Z(p)

. . . для Y(p)

. . .

X_ВХ

w

4. Степень полинома А(р) не превышает степени полинома В(р); знаменатель не содержит нулевого корня.

... для Z(p)

. . . для Y(p)

. . .

X_ВХ

w

. . .

2. Метод Кауэра позволяет проводить синтез, не разлагая полиномы числителями по нулям и полюсам.

Входное сопротивление цепной (или лестничной) схемы представляется непрерывной дробью: