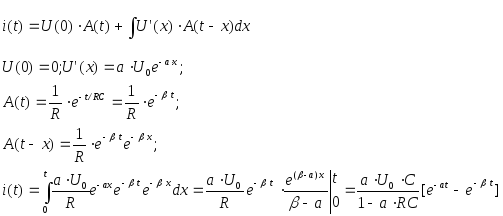Лекции / Лекции (2 семестр) / IMPULS

Лекция 5. Расчет переходных процессов при воздействии

импульсных ЭДС и ЭДС произвольной формы.

Воздействие импульсных напряжений - время действия импульса

меньше времени переходного процесса.

1 Импульсная функция нулевого порядка или единичная функция Хевисайда:

E1(t)=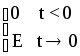

2. Импульсная функция первого порядка или d функция Дирака

K

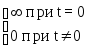
При этом:

Вспомним, что: или 1’(t)= d (t)

Производная функции Хевисайда равна d функции Дирака.

РАСЧЕТЫ ЦЕПЕЙ ПРИ ВНЕЗАПНОМ ВКЛЮЧЕНИИ ПОСТОЯННОГО НАПРЯЖЕНИЯ.

Они нам известны: i(t) =Е A(t)=Е Y(t)

Например

при включении RL цепи i(t) =(E/R)[1-]

или A(t) =Y(t) =(1/R)[1-]

при включении RC цепи i(t) =(E/R)

или A(t) =Y(t) =(1/R)

при включении RLC цепи A(t)=

A(t) или Y(t) является функцией времени, зависящей только от параметров цепи и называется ПЕРЕХОДНОЙ ПРОВОДИМОСТЬЮ.

В более общем случае

В этом случае говорят о ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКЕ цепи.

h(t) - функция временим зависящая от параметров цепи, определяющая реакцию цепи от воздействия единичного скачка напряжения.

РАСЧЕТЫ ЦЕПЕЙ ПРИ ВОЗДЕЙСТВИИ ИМПУЛЬСНОЙ ФУНКЦИИ

ПЕРВОГО ПОРЯДКА

Расчет проводят в предположении, что на цепь воздействуют последовательно два напряжения (прямой и обратной последовательности) бесконечно большой величины, включающиеся через так, что

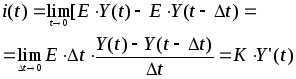
Например для RL цепи

Рассмотрим воздействие Кd(t) на RL цепь более подробно:

1(t)=1;

Следовательно: i(0)=K/L - т.е. за время под воздействием бесконечной ЭДС в RL цепи устанавливается ток равный i(0) .

Результат i(t)=K/L можно трактовать как уменьшениеие по экспоненте тока от начального значений (установившегося мгновенно) до нуля.

Величину Y’(t)=A’(t) называют ИМПУЛЬСНОЙ ПРОВОДИМОСТЬЮ или ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ.

Таким образом, при расчете воздействия импульса тока Кd(t) необходимо;

1. Расчитать реакцию при воздействии единичного напряжения, т.е. h(t)

2. Взять ее производную по времени h’(t) или A’(t)

3.Умножить на величину К , т.е. i(t) =К h’(t)

РАСЧЕТ ЦЕПЕЙ ПРИ ВОЗДЕЙСТВИИ ЭДС ПРОИЗВОЛЬНОЙ ФОРМЫ.

ИНТЕГРАЛ ДЮАМЕЛЯ.

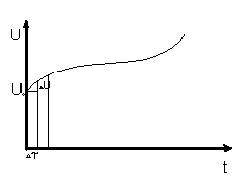
Напряжение можно представить как состоящее из последовательно включающихся ступеней. Тогда ток представляется как сумма токов от воздействия каждой ступени для малых значений интервала.

на интервале 0<t<

- приращение функции в момент времени t=k

Реакция системы, обусловленная воздействием равна

Cуммарная реакция r(t)=U(0)h(t)+=U(0)h(t)+

=U() для малых значений интервала

С учетом замены отношения приращений на производную в соответствующей точке, реакцию системы можно записать в виде:

r(t)=U(0)h(t)+

Уменьшим длительность интервала Dt В результате этого увеличится число разбиений n таким образом, что произведение nDt останется величиной постоянной.

Выполним предельный переход при ; nDt=const

Переходим от суммы к интегралу: r(t)=U(0)h(t)+=U(0)h(t)+

Второе выражение получено заменой переменных. Если взять интеграл по частям, то можно получить еще две формы: r(t)=U(t)h(0)+=U(t)h(0)+

Данные интегралы получили название интеграла Дюамеля. Выбор формы зависит от начальных условий, вида входного воздействия и импульсной или передаточной характеристики цепи.

Интеграл Дюамеля можно также получить исходя из импульсной функции нулевого порядка.

По определению передаточной функции системы равна реакции системы на d-функцию Дирака в области изображений :

H(p)=(p)

Запишем реакцию системы на единичное воздействие. Изображение1(t)=1/p.

Тогда R1(p)=H(p)/p ==> (p)=p R1(p)

Во временной области: 1’(t)=d(t)

Отсюда определим связь реакций системы на воздействие d-функции и 1(t):

r(t)=r1(t)+r1(0) d(t)

Для произвольного входного воздействия: R(p)=H(p)U(p)

Для определения реакции во временной области воспользуемся теоремой свертки (Если требуется определить оригинал от функции, представляющей собой произведение двух изображений, оригиналы для которых известны, то искомый оригинал определяется как свертка оригиналов) .

C учетом того, что реакция системы на единичное входное воздействие представляет собой переходную характеристику, можем записать:

r(t)= U(t)h(0)+

Заменой переменных и интегрированием по частям можно получить все остальные формы интеграла Дюамеля.

Необходимо отметить, что в двух формах интегральный член содержит переходную характеристику, в двух других импульсную.

Пример: на RC цепь воздействует напряжение U(t)=U0[1 ]

Решение операторным методом.

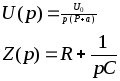
т.е. по теореме разложения:

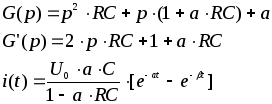
Решение с помощью интеграла Дюамеля.