Лекции / Лекции (2 семестр) / METOD-CHUV

Лекция 10. Чувствительность.

В общем виде под ЧУВСТВИТЕЛЬНОСТЬЮ понимают реакцию схемы на малое изменение параметра ее компонента.

Например, для схемы справедливо соотношение:

R_a

U₀/I₁=(R_a - R_b)/2

R_b Предположим,что R_a =100W,

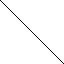
R_b =101W, I₁ =10A.Тогда-

U₀=5В.Если изменить номинал R_a на 10% т.е. R_a =90W, то U₀=55В.Схема очень чувствительна к изменению R_a.

Количественная оценка такого изменения параметров схемы при заданном изменении параметров компонента является КОЭФФИЦИЕНТОМ ЧУВСТВИТЕЛЬНОСТИ.

Сущестьвует ряд причин, по которым необходимо оценивать чувствительность при проектировании схем:

1. Как изменение какого-либо параметра схемы влияет на характеристику цели.

2. Сравнение чувствительности ряда схем, имеющих одну и ту же характеристику при номинальных значениях элементов схем.

3. Невозможность определения процента выхода годных схем, удовлетворяющих требованиям

4. Определение градиента функции, который используется при оптимизации схем.

5. Использование компонентов, работающих в сложных условиях окружающей среды.

Ограничим рассмотрение линейными схемами с сосредоточенными, не зависящими от времени, параметрами. Однако , для анализа нелинейных схем и схем, параметры которых зависят от времени, можно использовать те же методы при незначительной доработки.

Обычным приемом при количественной оценке чувствительности является ее представление в виде отношения изменения выходного параметра к изменению параметра компонента, выраженного в %

Для рассмотрения примера получаем 1100 % изменение выходного параметра при 10% изменении параметра компонента, т.е. чувствительность равна 110.

Пусть схема характеризуется функцией Y. Параметр компонента или элемента схемы изменен на некоторое значение DP_i ,в результате чего функция Y получила при изменении параметра P_i приращение DY.

Тогда :

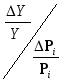
или эту величину называют коэффициентом

относительной чувствительности схемной

функции Y.

Рассмотрим общий случай. Пусть некоторая функция цепи зависит от n параметов:

Y=Y(P₁, ... P_n)

В качестве такой функции могут выступать входное и выходное сопротивления, передаточная характеристика, реакция цепи на некоторое входное воздействие ( во временной области) и т.д.

Значение фукции Y , как правило, зависит от частоты w₀ или времени . Данные параметры (w₀ и t₀ ) будут выступать в качестве независимых переменных.

Обозначим изменение каждого из переменных P₁, ... P_n через DP₁, ... DP_n соответственно. При этом предполагается, что изменение указанных переменных обуславливает изменение функции на DY.

Для определения связи между изменениями переменных и функции, разложим функцию Y в ряд Тейлора (предполагая наличие соответствующих производных). В результате:

(*)

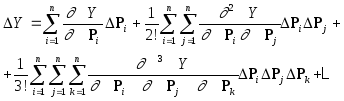Полученное соотношение справедливо, если существуют произодные функции по соответствующим переменным. Не смотря на то, что выражение для изменения DYопределяется бесконечным рядом, вклад членов ряда, начиная с третьего, много меньше по сравнению с первыми двумя членами. В результате ими можно пренебречь, без существенного снижения точности. Более того, при вычислении DYв большинстве случаев можно пренебречь даже вторым членом. В результате формула (*) принимает вид:

Абсолютная чувствительность S_i функции Y=Y(P₁, ... P_n) относительно параметра P_i определяется как частная производная:

Для оценки абсолютной чувствительности относительно всех переменных вводится вектор [G] (транспонированный градиент-вектор), который является вектором-строкой частных производных первого порядка:

Независимые параметры t и w₀ могут принимать ряд значений. Предположим, что независимый параметр принимает значений. Например, если в качестве независимого параметра выступает время, то:

Y= Y(P₁, ... P_n,t_i)= Y_i(P₁, ... P_n)

В таком случае функция у изменяется в зависимости от значения независимой переменной t . Вследствии этого вектор [G] заменяется матрицей размерности [m´n] членами которой являются частные производные. Данная матрица называется матрицей Якоби:

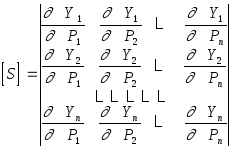
Эту матрицу называют матрицей чувствительности первого порядка

или просто матрицей чувствительности.

Если в выражении (*) производными второго порядка нельзя пренебречь, ввиду их существенного вклада в изменение функции Y, их называют коэффициентами чувствительности втрого порядка.

Производные второго порядка:

использует симметричной матрицы [H] размерности [n´n] вида:

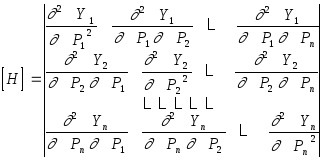
Матрица [H] называется матрицей Гесса или матрицей чувствительности

второго порядка.

При использовании матриц Якоби и Гесса соотношение (*) можно

переписать в виде:

DY=[G]^tD[P]+(1/2)´D[P]^t[H]D[P]

где [P]- вектор, элементами которого являются измерения DP_i :

D[P] = [DP₁DP₂ ... DP_n]^t

Относительная чувствительность.

ОТНОСИТЕЛЬНАЯ чувствительность S^r_i функции

Y= Y(P₁, ... P_n) относительно параметра P_i определяется как:

Если P_i или Y равно нулю, то данная формула непригодна.

В этом случае вводят полунормированные чувствительности:

Определение относительной чувствительности широко используется , так как с его помощью удобно вычислять коэффициенты чувствительности более высоких порядков.

Рассмотрим следствия, вытекающие из определения относительной чувствительности . Для этого запишем функцию схемы в показательной форме:

Y(jw)=½Y(jw)½´exp(jF)

Тогда:

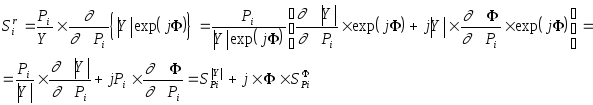
Полученное выражение позволяет для известной чувствительности функции схемы определить чувствительность как амплитудной, так и фазовой характеристики цепи.

Для случая, когда функция цепи может быть представлена в виде дробно-рациональной функции, заданной коэффициентами полиномов числителя и знаменателя

Y(s)=N(s)/D(s)

дифференциируя числитель и знаменатель по P_i

можно получить:

Таким образом, чувствительность функции может быть получена как разность чувствительности числителя и чувствительности знаменателя.

Относительная (нормированная) и полунормированная чувствительности широко используются для расчета схем, при которых необходимо сравнивать чувствительности относительно различных переменных, а полная чувствительность должна быть минимизирована.

ТЕОРЕМА: Сумма относительных чувствительностей S^r_i цепи равна единице для функций проводимости и сопротивления и равна 0 - для коэффициента передачи.

Данная теорема устанавливает важное ограничение на сумму относительных чувствительностей, при этом может осуществляться минимизация относительной чувствительности по ряду параметров или квадратичной чувствительности.

МЕТОДЫ РАСЧЕТА ЧУВСТВИТЕЛЬНОСТИ.

Расчет чувствительности связан с вычислением производных - сложная задача. Существует ряд методов ( со своими достоинствами и недостатками) как аналитических, так и ориентированных на использование ЭВМ.

I. Непосредственное дифференциирование.

Данный подход используется для простейших цепей, для которых достаточно просто получить аналитические зависимости.

Достоинства: эффективен в случае зависимости аналитического

выражения от или , как независимого параметра.

Недостатки: для сложных цепей получить явный вид функции-

задача трудоемкая ( если даже ее можно решить).

Дифференциирование функции в явном виде.

I I. Метод разностей.

Метод основан на использовании подхода, применяемого при численном вычислении производных как первого, так и более высоких порядков - замене производных на соответствующие приращения.

(**)

Для расчета чувствительности функции по каждому из параментов необходмо раз повести вычисления по формуле (**). С учетом того, что необходимо вычислять функцию при номинальных значениях параметров, такой подход потребует (n+1) вычислении функции.

Достоинства: реализация еа ЭВМ.

Недостатки:

1. Как правило, и малы, что приводит к существенным ошибкам.

2. Большой объем вычислений.

3. Точность можно повысить, однако, это приведет к еще большему объему вычислений.

I I I. Метод узловых потенциалов.

На основании метода узловых потенциалов запишем выражение для определения узловых потенциалов:

[j]=([A]´[Y]´[A]^t)^-1´[A]´([I]-[Y]´[E])

Получим выражение для определения изменения узловых потенциалов, обусловленное изменениями токов и напряжений в ветвях, а также изменениями узловых проводимостей.

Поскольку для линейных схем справедлив принцип суперпозиции, влияние [DY] ; [DI] и [DE] на изменение [Dj] можно считать независимыми.

Изменение узловых потенциалов в результате изменения [DI] и[DE]:

[Dj]=([A]´[Y]´[A]^t)^-1´[A]´([DI]-[Y]´[DE])

Уравнение получено для малых изменений токов и напряжения в ветвях по сравнению со значениями самих токов и напряжений.

При малых вариациях узловых проводимостей ветвей [Y] можно записать уравнение:

[A]´[DY]´[A]^t´[j]+[A]´[Y]´[A]^t´[Dj]=-[A]´[DY]´ ´[j]

из которого можно получить:

[Dj]=-([A]´[Ym]´[A]^t)^-1´[A]´{[DY]´([E]+[A]^t´[j])}

Результирующее уравнение для определения изменения узловых потенциалов будет иметь вид:

[Dj]=([A]´[Ym]´[A]^t)^-1´[A]´{[DI]-[Y]´[DE]-[DY]´([E]+[A]´[j])}

Введем обозначения:

[Y_Y]=([A]´[Ym]´[A]^t) - матрица узловых проводимостей;

[DY_Y]=([A]´[DY]´[A]^t) - матрица изменения узловых

проводимостей;

[I_Y]=[A]´([I]-[Y]´[E]) - матрица узловых токов;

[DI_Y]=[A]´([DI]-[Y]´[DE]) - матрица изменения узловых токов.

В этом случае:

[Dj]=[Z_Y]´{[DI_Y]-[A]´[DY]´[E]-[A]´[DY]´[A]´[j]}

В дальнейшем индекс "Y" можно опустить:

[Dj]=[Z]´{[DI]-[A]´[DY]´[E]-[A]´[DY]´[A]´[j]}

Полученное соотношение позволяет определить чувствительность первого порядка при вариациях токов и напряжений независимых источников [E] и [I], а также при изменениях параметров матрицы узловых проводимостей.

После определения изменения узловых потенциалов, можно определить чувствительность.

Достоинства:

1. Базируется на МУП , поэтому полученные при расчете матрицы могут быть использованы для оценки чувствительности.

2. Реализуем на ЭВМ.

Недостатки: требует обращения матрицы узловых проводимостей.

При плохой обусловленности матрицы [Y] данная

процедура приводит к существенным ошибкам вычи-

сления.

Существует метод, позволяющий устранить указанный недостаток: метод присоединной схемы.