Лабораторная работа №5.

Метод Ньютона.

Метод Ньютона – один из итерационных методов, отличающийся идейной простотой и быстрой сходимостью. Правило построения итерационной последовательности ( х_к ) получают из геометрических соображений , отсюда второе название этого метода – метод касательных.

Одномерный случай. Дано уравнение . Преобразуем его к виду и обозначим . Пусть найдена точка х_к - к-ое приближение к корню х^* , положим , тогда .

Таким образом, имеем : . Это и есть итерационная процедура Ньютона.

Геометрический смысл метода Ньютона: приближения к корню х^* осуществляется по абсциссам точек пересечения касательных к графику данной функции, проводимых в точках, соответствующим предыдущим приближениям.

Х_к

Х_к-1

Х_к+1

Х^*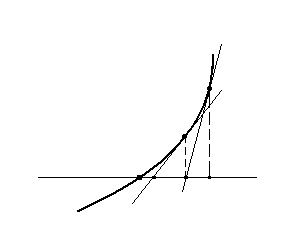

Многомерный случай. Пусть задана система уравнений:

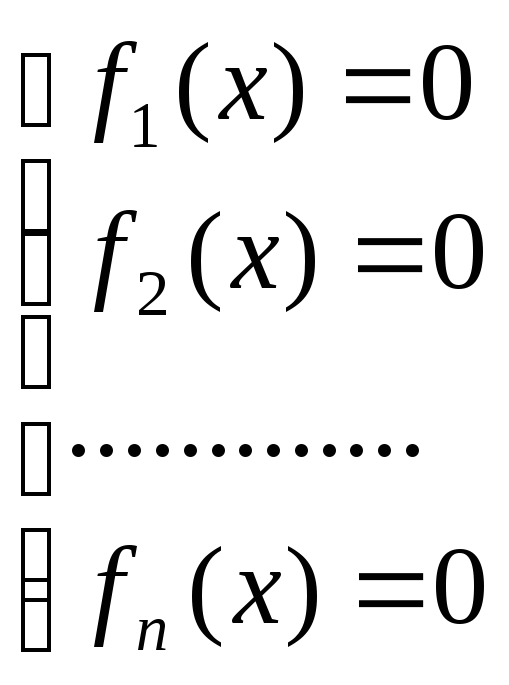где

Эта система эквивалентна уравнению , где - вектор-функция от векторного аргумента.

Аналог одномерного случая:

где 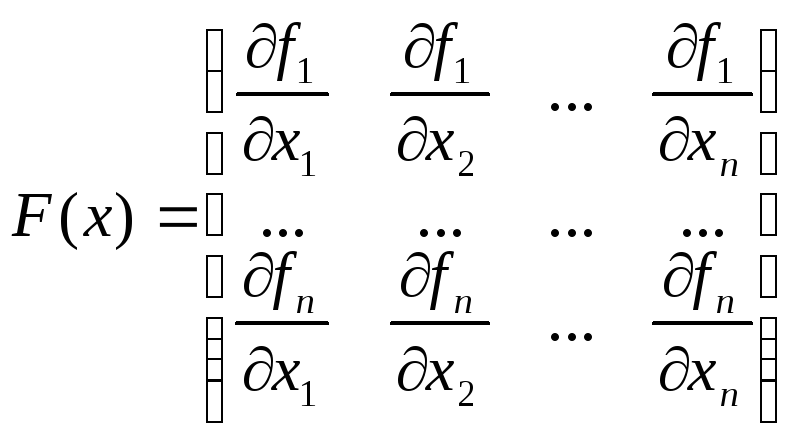- матрица Якоби .

Задание к лабораторной работе.

1.Разобраться в работе функции Nuton, которая вычисляет корни полинома с помощью одномерной итерационной процедуры Ньютона. В качестве параметров ей передаются коэффициенты многочлена, начальное приближение Х₀ и необходимая точность Ерs . Найти корни уравнения =0.

2.Разобраться в работе функции NutonM, реализующей многомерный случай использования метода Ньютона. Параметры функции :

PolynomHandle – строковая константа, соответствующая файлу-функции, содержащему описание вектор-функции ;

EcobyHandle – строковая константа, соответствующая файлу-функции, описывающему матрицу Якоби для данной системы ;

X0 – вектор начальных приближений ;

Eps – необходимая точность.

3. С помощью NutonM найти решения систем, создав соответствующие файлы, описывающие и матрицу Якоби:

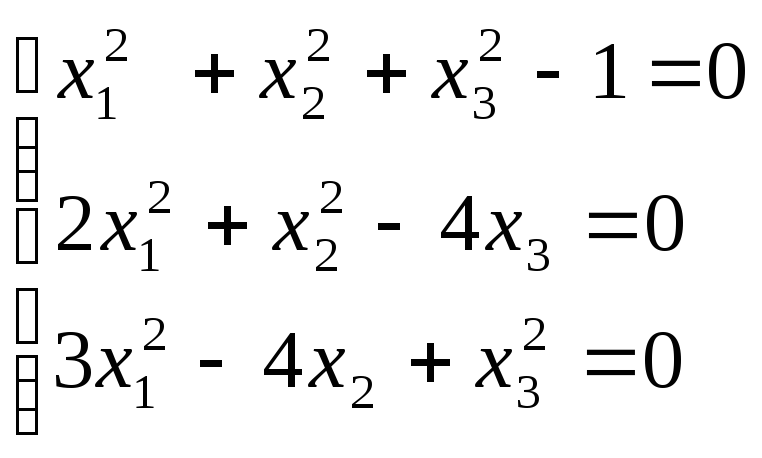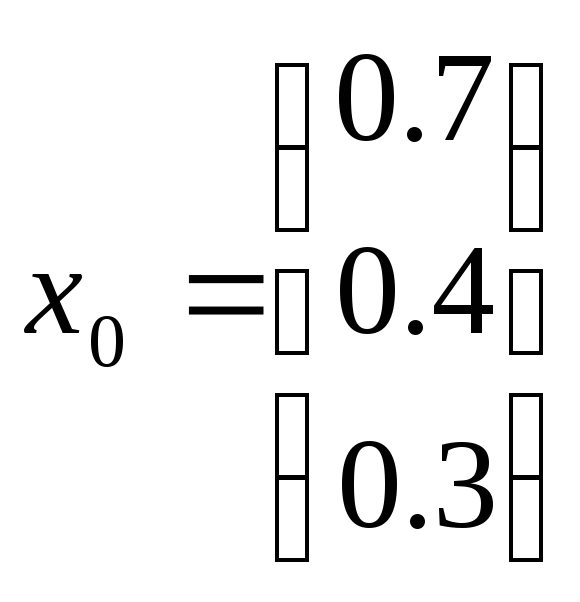
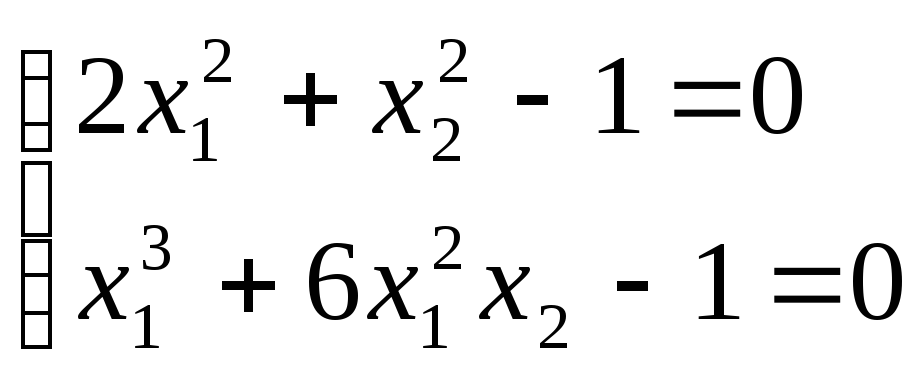в качестве начального приближения взять

в качестве начального приближения взять

EcobyHandle1.m

function [F] = EcobyHandle(X0)

F(1,1) = 2*X0(1);

F(2,1) = 4*X0(1);

F(3,1) = 6*X0(1);

F(1,2) = 2*X0(2);

F(2,2) = 2*X0(2);

F(3,2) = -8*X0(2);

F(1,3) = 2*X0(3);

F(2,3) = -8*X0(3);

F(3,3) = 2*X0(3);

EcobyHandle.m

function [F] = EcobyHandle(X0)

F(1,1) = 4*X0(1);

F(2,1) = 3*(X0(1)^2);

F(1,2) = 2*X0(2);

F(2,2) = 6*(X0(1)^2);

PolynomHandle1.m

function [f] = PolynomHandle(X0)

f(1) = X0(1)^2 + X0(2)^2 + X0(3)^2 - 1;

f(2) = 2*X0(1)^2 + X0(2)^2 -4*X0(3)^2;

f(3) = 3*X0(1)^2 -4*X0(2)^2 + X0(3)^2;

PolynomHandle.m

function [f] = PolynomHandle(X0)

f(1) = 2*X0(1)^2 + X0(2)^2 - 1;

f(2) = 3*X0(1)^2 + 6*(X0(1)^2)*X0(2) - 1;

NutonM.m

function y=NutonM(PolynomHandle, EcobyHandle,X0,Eps)

NumberOfIteracy=0;

OldDelta=0;

while(1)

Ecoby=feval(EcobyHandle,X0);

f=feval(PolynomHandle,X0);

[Strok Stolbcov]=size(f);

if (Strok==1)&(Stolbcov~=1)

f=f';

end;

if (Strok~=1)&(Stolbcov~=1)

error('wrong polynomial value');

break;

end;

if det(Ecoby)==0

error('inverse Ecoby matrix doesn''n exist')

break;

end;

X=X0'-(Ecoby^-1)*f; %the calculation of the next approximation

if norm(X-X0')<Eps; %the precision of the aproximation has been achieved

break;

end;

if OldDelta<norm(X-X0')%if the aproximation is worse

NumberOfIteracy=NumberOfIteracy+1;%error can worse a few times

end;

OldDelta=norm(X-X0');

X0=X';

%if the correct answer cannnot be obtained

if (abs(X0(1))==Inf)|(abs(X0(1))>=NaN)|(NumberOfIteracy>100)

error('there is no answer for this system')

break;

end;

end;

format long y;

y=X;

Распечатка результатов выполнения в среде MatLab

Решение первой системы:

>> NutonM('PolynomHandle', 'EcobyHandle', [0.7 0.4 0.3], 1)

ans =

0.61785714285714

0.63750000000000

0.60833333333333

>> NutonM('PolynomHandle', 'EcobyHandle', [0.7 0.4 0.3], 0.01)

ans =

0.61237243617965

0.59161027791617

0.52443603508544

>> NutonM('PolynomHandle', 'EcobyHandle', [0.7 0.4 0.3], 0.0001)

ans =

0.61237243569579

0.59160797831443

0.52440442503777

Решение второй системы:

>> NutonM('PolynomHandle', 'EcobyHandle', [0.6 0.2], 1)

ans =

0.75218855218855

-0.11313131313131

>> NutonM('PolynomHandle', 'EcobyHandle', [0.6 0.2], 0.01)

ans =

0.69820704478312

-0.15815850640665

>> NutonM('PolynomHandle', 'EcobyHandle', [0.6 0.2], 0.0001)

ans =

0.69821163854414

-0.15811710014957

>> NutonM('PolynomHandle', 'EcobyHandle', [0.6 0.2], 0.001)

ans =

0.69820704478312

-0.15815850640665