ЛАБОРАТОРНАЯ РАБОТА 3. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

ЗАДАНИЯ

1. Вычисление интерполяционного многочлена Лагранжа в точке.

Изучить функцию lagr, разобраться в том, как данная подпрограмма выполняет вычисление интерполяционного многочлена Лагранжа.

Программа:

%Задание 3.1

'Задание 3.1'

clear;

global lagrange;

global newton;

lagrange = 0;

newton = 1;

X = [0 2 3 5];

F = [1 3 2 5];

t = 2.5;

p = lagr(X,F,t);

p

Результат:

p = 2.4792

2.Построение графика интерполяционного многочлена.

Используя вызовы функции lagr, создать собственную ­функцию lag, которая формирует массив значений интерполяционного полинома для заданного набора (массива) значений аргумента T: function P = lag(X,F,T), где P - массив значений полинома, T - массив значений аргумента полинома; X, F - массивы, содержащие соответственно абсциссы и ординаты узлов интерполяции.

Программа:

%Задание 3.2

'Задание 3.2'

T = rand(100)*10;

p = interPol(T, lagrange);

p;

figure(1);

plot(p);

p = interPol(T, newton);

p;

figure(2);

plot(p);

Результат:

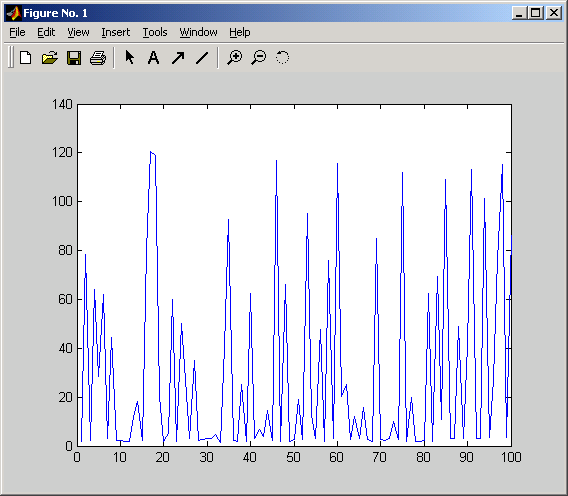
• по форме Лагранжа

• по форме Ньютона

3. Ошибка интерполяции по равноотстоящим узлам.

Для f(x) = cos(x), a = 0, b = 2, h = /100, с использованием функций lag или newt получить массив значений интерполяционных полиномов L_n(x) порядков n=5 и n=8 по равноотстоящим узлам:

x_i = a + i(b-a)/n, i = 0,1,…,n.

Программа:

%Задание 3.3

'Задание 3.3'

clear;

global a;

global b;

global h;

a = 0;

b = 2*pi;

h = pi/100;

n = input ('Введите порЯдок n = ');

X = XLagr(n);

F = FLagr(X, n);

j = 1;

abcissa = [a:h:b];

for i = a:h:b,

Rn(j) = sin(i) - lagr(X, F, i);

j = j + 1;

end

figure(3);

plot(abcissa, Rn);

'МаксимальнаЯ ошибка'

erMax = abs(max(Rn))

'Точка, в которой находитсЯ максимальнаЯ ошибка'

j = 1;

for i = a:h:b,

if abs(Rn(j)) == erMax

argErMax = i

break;

end

j = j + 1;

end

Xteor = erMax - X;

u=prod(Xteor);

'ТеоретическаЯ ошибка'

erTeor=abs(1/factorial(n)*u)

Результат:

Для степени 8

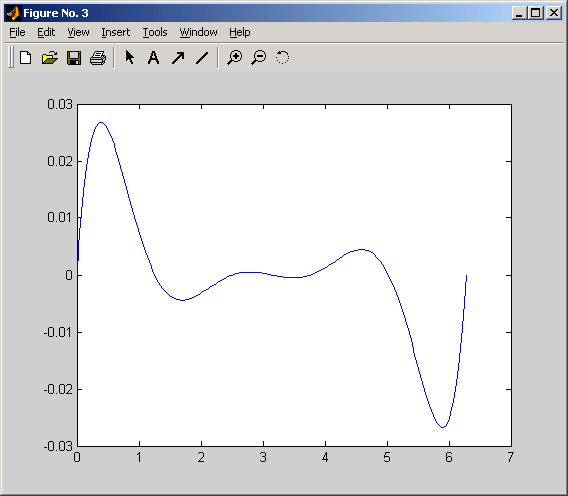
Для степени 5.

Максимальная ошибка в точке t = 0.3770 и равна erMax = 0.0267

Теоретическая ошибка erMaxTeor = 0.0798

4. Ошибка интерполяции по Чебышевским узлам.

Выполнить предыдущий пункт задания, но в качестве узлов интерполяции взять корни многочлена Чебышева T _n+1(x):

, i = 0,1,…,n

(n - порядок интерполяционного полинома). Сравнить значения наибольших ошибок со значениями, полученными в предыдущем пункте.

Программа:

%Задание 3.4

'Задание 3.4'

X = XCheb(n);

F = FLagr(X, n);

j = 1;

for i = a:h:b,

Rn(j) = sin(i) - lagr(X, F, i);

j = j + 1;

end

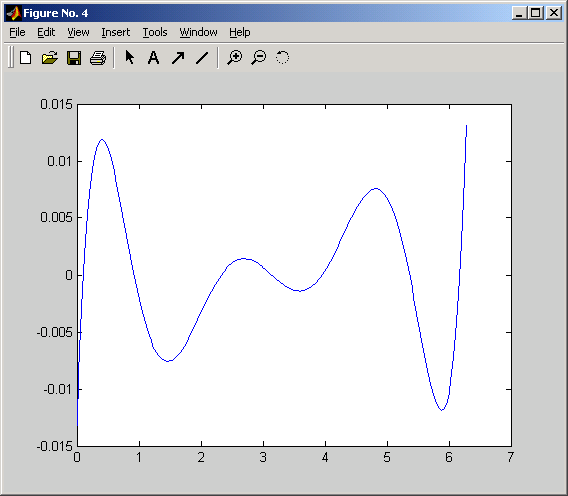
figure(4);

plot(abcissa, Rn);

'МаксимальнаЯ ошибка'

erMax = abs(max(Rn))

'Точка, в которой находитсЯ максимальнаЯ ошибка'

j = 1;

for i = a:h:b,

if abs(Rn(j)) == erMax

argErMax = i

break;

end

j = j + 1;

end

Результат:

Максимальная ошибка в точке t = 0.3770 и равна erMax = 0.0267 для степени 5.