Метод верхней релаксации.

Будем решать данную систему методом верхней релаксации, который является обобщением метода Зейделя. Для ускорения сходимости метода Зайделя его несколько модифицируют введением параметра сходимости .

Двухслойное каноническое итерационное уравнение с параметром >0 записывается в виде:

,k = 0,1,…; z⁰  H_h

A=D+L+T, аB= D+L. В частном случае, при =1 получаем метод Зайделя, при

 >1 – собственно метод верхней релаксации, где

; ;

Применительно к нашей конечно-разностной схеме, метод верхней релаксации записывается в виде:

( 1 )

В этой итерационной процедуре (1) по методу верхней релаксации сначала на (k+1)-й итерации находим промежуточное значение по уже известным на данном шаге значениям сеточной функциис помощью первой формулы (1), а затем окончательное значениенаходим по второй формуле (1). Итерационный процесс сходится для всех, удовлетворяющих неравенству1 < < 2. Вопрос о выборе оптимального значенияиз данного промежутка, которое обеспечивало бы максимальную скорость сходимости метода верхней релаксации, требует анализа спектральных характеристик оператора А, что является достаточно сложным в теоретическом отношении. Но иногда удается получить значения близкие к оптимальным, в результате машинного эксперимента при варьировании параметрав интервале (1,2). Метод верхней релаксации чрезвычайно просто алгоритмизуется для численных расчетов на ЭВМ. Он реализован в программе kurs.m.

Применительно к конкретной задаче оптимальное значение параметра сходимости было определено из машинного эксперимента. С помощью программы getep.m, предназначенной для изучения скорости сходимости в зависимости от параметра сходимости, было найдено оптимальное значение параметра. За основу алгоритма было взято решение данного уравнения на сетке фиксированного размера за фиксированное число шагов.

Результаты выполнения программы занесены в Таблицу 1.

	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
	0.0269	0.0239	0.0198	0.0145	0.0084	0.0027	0.0041	0.0173	0.0934	0.3996	1.5384
	1.41	1.42	1.43	1.44	1.45	1.46	1.47	1.48	1.49
	0.0077	0.0071	0.0065	0.0059	0.0053	0.0048	0.0042	0.0037	0.0031
	1.51	1.52	1.53	1.54	1.55	1.56	1.57	1.58	1.59
	0.0029	0.0021	0.0018	0.0015	0.0013	0.0018	0.0023	0.0029	0.0035
	1.541	1.542	1.543	1.544	1.545	1.546	1.547	1.548	1.549
	0.0014	0.0014	0.0014	0.0013	0.0013	0.0013	0.0012	0.0012	0.0012
	1.551	1.552	1.553	1.554	1.555	1.556	1.557	1.558	1.559
	0.0012	0.0014	0.0014	0.0015	0.0015	0.0016	0.0016	0.0017	0.0017

Таблица 1: Результаты выполнения программы getep.m. Из результатов видно, что оптимальное значение параметра сходимости находится на интервале (1.547,1.552).

Для нахождения более точного значения используем программу scanmu.m, в которой была получена зависимость погрешности (которую можно связать с величиной, обратной скорости сходимости) от параметра сходимости. Графики этой функции на различных интервалах представлены на рисунках.

Рис.1. Нахождение оптимального значения параметра сходимости с помощью программы scanmu.m на интервале (1,2) с точностью  = 0.1. В результате мы получили, что оптимальное значение параметра сходимости находится на интервале (1.4,1.6), что совпадает с нашими расчетами в программе getep.m приведенными выше.

Рис.2. Нахождение оптимального значения параметра сходимости с помощью программы scanmu.m на интервале (1.4,1.6) с точностью  = 0.01. В результате мы получили, что оптимальное значение параметра сходимости находится на интервале (1.54,1.56).

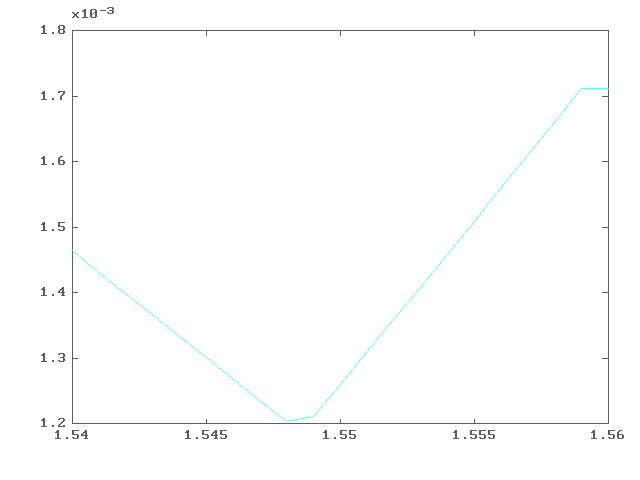
Рис.3. Нахождение оптимального значения параметра сходимости с помощью программы scanmu.m на интервале (1.54,1.56) с точностью  = 0.001. В результате мы получили, что оптимальное значение параметра сходимости находится на интервале (1.545,1.55).

Рис.4. Нахождение оптимального значения параметра сходимости с помощью программы scanmu.m на интервале (1.545,1.55) с точностью  = 0.0001. В результате мы получили, что оптимальное значение параметра сходимости находится на интервале (1.548,1.549).

Таким образом, было получено оптимальное значение параметра сходимости. Это значение и используется при конечных вычислениях в программеkurs.m. График найденной функции и её линии уровня представлены на рисунках.

Рис.5. Изображение найденной функции с помощью программы kurs.m. на сетке с параметрамиM =N = 10,  = 0.001,  = 1.5485.

Рис.6. Изображение линий уровня функции с помощью программы kurs.m. на сетке с параметрамиM =N = 10,  = 0.001,  = 1.5485.

Матрица решения заданного уравнения для M=N=20, приведена в

Таблице 2.