3.3. Метод сеток

Метод сеток состоит в сведении решения краевой задачи к решению алгебраических уравнений для так называемой сеточной функции. Для этого область Gнепрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги.

Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых и будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки –узлы сетки. Функция, определенная в узлах сетки, называетсясеточной функцией.

Пусть ω_h– сетка в некоторой областиG,H_h – линейное пространство сеточных функций, заданных наω_h;H₀ –линейное пространство гладких функций (x); - норма вH₀; - норма вH_h. Предполагается, что:

1. существует оператор проектирования P_hтакой, чтоP_h=_hH_h для любогоH₀;

2. нормы и согласованы, т. е.||P_h || = .

Рассмотрим некоторый дифференциальный оператор λ, заданный вH₀, и операторλ_h, преобразующий сеточную функцию _h в сеточную функциюλ_hh, заданную наω_h.

Погрешностью аппроксимации оператора λразностным операторомλ_hназывается сеточная функцияψ_h = λ_hh – (λ)_h, в сеточном пространствеH_h, где _h= P_h, (λ)_h= P_h(λ), - любая функция изH₀. Если при этом

|| ψ_h ||_h=|| λ_hh-(λ)_h ||_h=O(h^m), то разностный операторλ_hаппроксимирует дифференциальный операторλс порядкомm>0.

При формулировке соответствующей разностной задачи необходимо аппроксимировать не только дифференциальное уравнение, но и краевые и начальные условия.

3.4. Разностная аппроксимация простейших дифференциальных операторов

Пусть дан линейный дифференциальный оператор L, действующий на функциюv=v(x).Заменяя входящие вLv производные разностными отношениями, получим вместоLvразностное выражениеL_hv_h, являющееся линейными комбинациями значений сеточной функцииv_hна некотором множестве узлов сетки, называемомшаблоном. Такая приближенная заменаLv наL_hv_hназываетсяаппроксимацией дифференциальногооператора разностным оператором (или разностной аппроксимацией оператораL).

Изучение разностных аппроксимаций оператора Lвначале производят локально, т.е. в любой фиксированной точкеxобласти_h. Прежде чем приступать к разностной аппроксимации оператора необходимо выбратьшаблон, т.е. указать множество соседних с узломх_iузлов, в которых значения сеточной функцииv_h(x_i)=v(x_i)могут быть использованы для аппроксимации оператораL.

Обозначим (x)=L_hv(x)-Lv(x)приh0. Величина(x)называется погрешностью разностной аппроксимацииLvв точкех.

Говорят, что L_hаппроксимирует дифференциальный операторLспорядкомm>0в точкех, если(x)=L_hv(x)-Lv(x)=О(h^m).

Аппроксимируем данное уравнение, используя пятиточечный шаблон "крест".

Аппроксимация дифференциального оператора на этом шаблоне имеет вид: ,

где h₁- шаг сетки поiиh₂- шаг сетки поj. Погрешность аппроксимации.

Если известна искомая функция U(x,y) в точках:

(i-1,j); (i+1,j); (i,j+1); (i,j-1),

то значение U(x,y)в точке(i,j)может быть приближенно найдено следующим образом:

,

где .

Это уравнение должно выполняться для всех внутренних узлов сетки, т.е. для. Для того, чтобы система стала полностью определенной, надо дополнить ее уравнениями, полученными при аппроксимации начальных и граничных условий.

Аппроксимация 1-го начального условия.

Начальное условие 3-го рода выглядит следующим образом . Для его аппроксимирования разложимU(x,y) в окрестности точки (x,0) в ряд Тейлора:

Используя исходное уравнение и граничное условие, получим:

Перейдем к конечным разностям, записываемым в узле (i,1), т.е. на первом слое:

отсюда

.

Аппроксимация 1-го граничного условия.

Граничное условие 3-го рода выглядит следующим образом . Для его аппроксимирования разложимU(x,y) в окрестности точки (x,) в ряд Тейлора:

Используя исходное уравнение и граничное условие, получим:

Перейдем к конечным разностям, записываемым в узле (i,M-1), т.е. на предпоследнем слое:

отсюда

Аппроксимация 2-го граничного условия.

Граничное условие первого рода выглядит следующим образом:. Оно аппроксимируется следующим равенством:

j=0,1,2,3….N

Аппроксимация 2-го начального условия.

Граничное условие второго рода выглядит следующим образом: (в нашем случае). Для его аппроксимирования разложимU(x,y) в окрестности точки (0,у) в ряд Тейлора:

Используя исходное уравнение и граничное условие, получим:

Перейдем к конечным разностям, записываемым в узле (1,j), т.е. на первом слое:

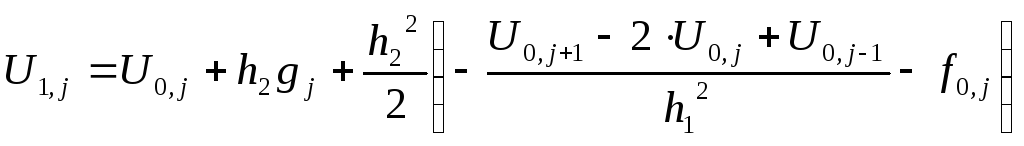
отсюда