§2 Метод сеток.

Метод сеток состоит в сведении решения краевой задачи к решению алгебраических уравнений для так называемой сеточной функции. Для этого область G непрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги. Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых и будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки – узлы сетки. Функция, определенная в узлах сетки, называется сеточной функцией.

Пусть ω_h – сетка в некоторой области G, H_h – линейное пространство сеточных функций, заданных на ω_h ; H₀ –линейное пространство гладких функций (x) ; - норма в H₀ ; - норма в H_h. Предполагается, что:

1. существует оператор проектирования P_h такой, что

P_h=_hH_h для любого H₀

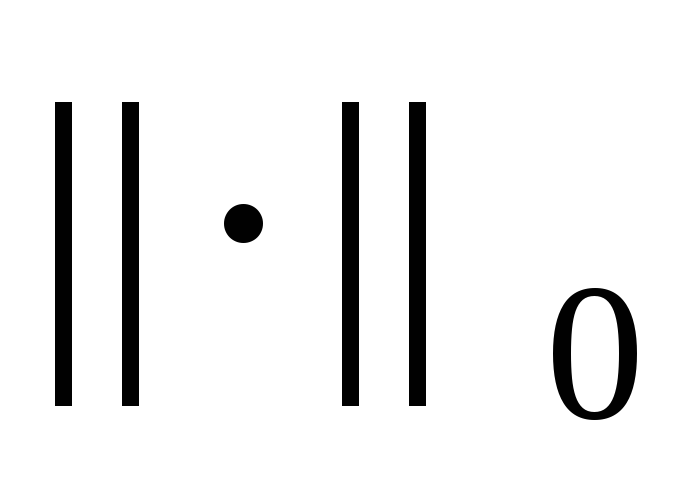2. нормы и 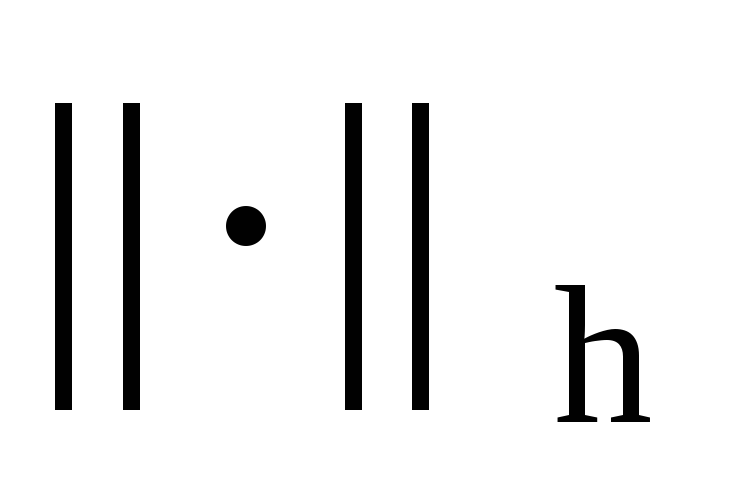согласованы, т. е.

||P_h || =

Рассмотрим некоторый дифференциальный оператор λ, заданный в H₀, и оператор λ_h, преобразующий сеточную функцию _h в сеточную функцию λ_hh, заданную на ω_h.

Погрешностью аппроксимации оператора λ разностным оператором λ_h называется сеточная функция ψ_h = λ_hh – (λ)_h, в сеточном пространстве H_h , где _h= P_h, (λ)_h= P_h(λ), - любая функция из H₀. Если при этом

|| ψ_h ||_h= ||λ_hh - (λ)_h||_h = O(h^m), то разностный оператор λ_h аппроксимирует дифференциальный оператор λ с порядком m>0.

При формулировке соответствующей разностной задачи необходимо аппроксимировать не только дифференциальное уравнение, но и краевые и начальные условия.

§3 Разностная аппроксимация простейших дифференциальных операторов.

Пусть дан линейный дифференциальный оператор L, действующий на функцию v=v(x). Заменяя входящие в Lv производные разностными отношениями, получим вместо Lv разностное выражение L_hv_h, являющееся линейными комбинациями значений сеточной функции v_h на некотором множестве узлов сетки, называемом шаблоном. Такая приближенная замена Lv на L_hv_h называется аппроксимацией дифференциального оператора разностным оператором ( или разностной аппроксимацией оператора L).

Изучение разностных аппроксимаций оператора L вначале производят локально, т.е. в любой фиксированной точке x области _h. Прежде чем приступать к разностной аппроксимации оператора необходимо выбрать шаблон, т.е. указать множество соседних с узлом х_i узлов, в которых значения сеточной функции v_h(x_i)=v(x_i) могут быть использованы для аппроксимации оператора L.

Обозначим: (x)=L_hv(x)-Lv(x) при h0. Величина (x) называется погрешностью разностной аппроксимации Lv в точке х.

Говорят, что L_h аппроксимирует дифференциальный оператор L с порядком m>0 в точке х, если

(x)=L_hv(x)-Lv(x)=О(h^m).

Выполнение работы.

1. Классификация краевой задачи и её физический смысл

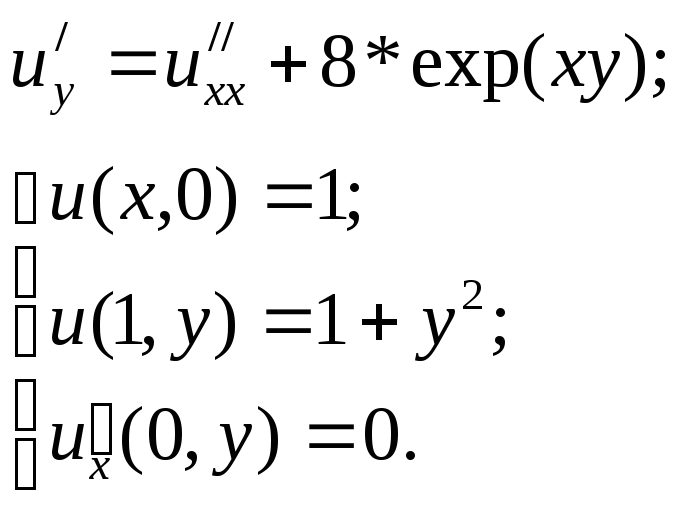
Данное уравнение является уравнением параболического типа и физически отражает процесс распределения тепла в однородном стержне длиной единица. Его решением является функция - значение температуры стержня в точке в момент времениy, где , .

- начальное условие, означающее, что в начальный момент времени температура стержня была равна единице, - граничное условие первого рода, означающее, что в течение всего процесса температура на правом конце стержня изменялась по заданному закону.

- граничное условие второго рода, означающее, что поток тепла на левом конце стержня равен нулю, то есть нет теплообмена левого конца стержня с окружающей средой.

- плотность источников тепла.