Система (2.9) имеет бесконечное множество решений, так как количество уравнений в ней всегда меньше числа неизвестных. Для выделения какого-либо одного решения минимизируется функционал

f=(T f,T f)_H=||T f||²_H=min ,(2.10)

который путем выбора подходящего оператора Т характеризует меру качества решения f.

Из всевозможных функций f, удовлетворяющих условию (2.9), выбирают в качестве решения функцию f, обеспечивающую минимум функционалу качества. Оператор Т в формуле (2.10) обычно имеет вид дифференциального оператора P-гo порядка

, (2.11)

где ₁+₂=P.

Существующие методы решения задачи восстановления функции отличаются выбором пространства Н, в котором предполагается искать решение, и выбором оператора Т. В данной работе для восстановления функции x,y) в двумерной области  (прямоугольник размером n₁n₂) были использованы следующие методы:

Интерполяционный сплайн. При P=2 оператор Т определяется следующим выражением: , (2.12).

Решение принадлежит гильбертову пространству со скалярным произведением,

и имеет вид: , (2.13)

где r_i(x, у) - расстояние между текущей точкой В_i области  и фиксированной точкой В (узел регулярной сетки, в которой восстанавливается значение функции).

Коэффициенты a₁,...a_n, ₁, ₂, ₃ находятся из решения системы уравнений , (2.14).

Основным недостатком метода является плотная заполненность матрицы коэффициентов системы (2.14).

Метод конечных элементов.

Решение ищется приближенно (с заданной точностью) в конечномерном пространстве Н^h (размерностью N) с базисом, элементами которого являются финитные функции (базис типа конечных элементов, N=n₁  n₂)

, (2.15)

i = 1, ... n₁; j = 1, ... n₂,

где ,(2.16)

и имеет вид: 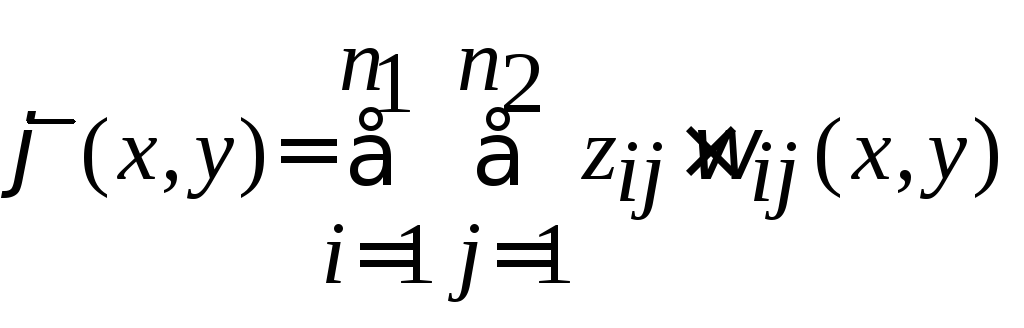,(2.17)

где z_ij - коэффициенты разложения по базису типа конечных элементов, вычисление которых зависит от выбора нормы пространства Н, а следовательно, и функционала качества.

В статье приводятся результаты вычисления, полученные с помощью функционалов качества следующих двух видов:

, (2.18)

, (2.19)

где  - параметр регуляризации.

Минимизация функционалов качества (2.18) и (2.19) приводит к системе линейных уравнений вида.(2.20).

Выбор базиса типа конечных элементов обеспечивает разреженность матриц В и G. Это является основным преимуществом метода конечных элементов.

Решение системы (13) выполнялось методом итераций с использованием следующего выражения: , (2.21)

где D – диагональная матрица с элементами диагонали ab_ij+g_ij , i = j (b_ij , g_ij- элементы матриц В и G соответственно); B'+G' - матрица , диагональные элементы которой заменены нулями.

Параметр регуляризации  в обоих случаях выбирается так, чтобы получить минимальные значения в . Отметим, что в общем случае матрицаG вырожденная. Поэтому по мере уменьшения  сходимость итераций ухудшается. Надежность определения коэффициентов разложения по базису типа конечных элементов z_ij, т. е. восстановленных значений функции в узлах сетки, зависит от плотности распределения исходных данных в области .

Разреженность матрицы позволяет значительно уменьшить объем использованной памяти ЭВМ и ускорить процесс вычисления.

Анализ результатов вычисления.

1. Наиболее точные результаты получены методом интерполяционного сплайна. При n = 80 среднее квадратическое отклонение m = 0,11 и среднее арифметическое отклонение  = - 0,01. Удовлетворительные результаты получены и для n = 20 (m = 0,42;  = - 0,08). Однако, неравномерное распределение исходной информации существенно влияет на точность аппроксимации.

2. Из анализа результатов, полученных методом конечных элементов при  =1 и n = 80 можно сделать вывод, что использование функционала качества вида (2.19) дает более качественные результаты (m = 0,46;  = 0,01) по сравнению с функционалом качества (2.18) (m = 1,16;  = 0,01).

3 Оптимизация параметра регуляризации ( = 1/64) позволяет значительно повысить точность метода конечных элементов. Для функционала качества (2.18) до m=0,28 и  = - 0,01, n = 80, а для (2.19) точность решения почти равна точности метода интерполяционного сплайна (m = 0,18;  = - 0,01, n = 80). При этом сохраняются численные преимущества метода конечных элементов. При недостаточном количестве исходной информации (n = 20) метод конечных элементов дает неудовлетворительные результаты.

Таким образом, при наличии большого числа измерений задачу целесообразно решать методом конечных элементов с функционалом качества (2.19) и с выбором подходящего значения параметра регуляризации . При недостатке исходных данных задачу рекомендуется решать с использованием интерполяционного сплайна.

Из аналитической геометрии.

ПОЛИНОМЫ параметрические Полиномы Бернштейна, Безье, поверхности Кунса

Кривые Безье .Кривые Безье названы по имени французского математика Пьера Безье, впервые предложившего их в начале 70-х годов пр.века фирме «Рено» для моделирования обводов кузова легкового автомобиля. (P. de Casteljau. Courbes et surfaces a poles. Technical Report, A. Citroen, Paris, 1963). Уравнение кривой Безье n-го порядка в многомерном пространстве для каждой координаты запишется так: (1)

где r(t) - параметрически задаваемая координата; - координатыi опорных точек (число которых равно );t - параметр, который принимает значения от 0 до 1, чем больше значений, тем глаже кривая. Вот плоская кривая Безье третьего порядка c четырьмя опорными точками.

Найти,( где-то писал) о постоянной пропорции построения кр. безье и вставить

Полиномы Бернштейна (Сергей Натанович( 5.3.1880- 26.10.68 Новодевичье Кл.) одессит, академик, один из величайших математиков 20 века преп. Харьков, Ленинград, Париж, Москва) предложил (опубликовано в 1912г. Сообщения Харьковского математ. Общества “Demonstration du theoreme de Weierstrass fondee sur la calcul des probalites”).

Линейная комбинация базисных полиномов Бернштейна (или с подстановкой базисных полиномов: ) называетсямногочленом (полиномом) Бернштейна или многочленом в форме Бернштейна степени n. Коэффициенты называютсякоэффициентами Бернштейна или коэффициентами Безье.

(n + 1) базисных многочленов Бернштейна степени n находятся по формуле , где— биномиальный коэффициент. Базисные многочлены Бернштейна степениn образуют базис для линейного пространства Π_n многочленов степени n. Вот некоторые базисные полиномы Бернштейна:

Все рис пропали

Рис. Кубическая кривая Безье и ее годограф (первая производная, тоже кривая Безье, r и ∆r –векторы ее управляющих точек)

Для конструирования криволинейных поверхностей с помощью стандартных параметрических полиномов, полиномов Бернштейна и NURBS (NonUniform Rational B-Spline )в системах геометрического моделирования применяют три основных метода:

Метод тензорного произведения (tensor product surfaces);

Основные свойства рациональных поверхностей Безье:

Поверхность полностью определяется набором вершин характеристической сетки .

Поверхность лежит в выпуклой оболочке точек .

Самой поверхности в общем случае принадлежат только четыре угловые точки сетки. В этих точках касательные плоскости поверхности совпадают с плоскостями угловых граней характеристической сетки.

Граничными кривыми порции поверхности являются рациональные кривые, управляемые набором точек и соответствующих весов.

Рациональная поверхность Безье аффинно- и проективно-инвариантна.

Формой поверхности можно управлять подбором вершин характеристической сетки и соответствующих весовых коэффициентов

Каркасный метод (lofting surfaces); поверхность определяется семейством кривых. Уравнение поверхности записывается в виде: где все???

или

Метод булевой суммы (поверхности Кунса). Задают два семейства граничных кривых (в инаправлениях). Уравнение поверхности Кунса имеет вид:

Граничные кривые представляют собой рациональные кривые Безье, управляющие точки которых получены с помощью методов интерполяции исходных точек поверхности, внутренние точки порции поверхности вычисляются с помощью билинейной интерполяции в двух направлениях. Обобщением поверхностей Кунса являются поверхности, интерполирующие всю заданную криволинейную сетку (поверхности Гордона)

Нелинейные поверхности Кунса (привести картинки )

Кубическая поверхность Безье (Денискин Ю.И. МГАИ (технический университет))

Геометрия построения плоской кривой Безье (полиномы Бернштейна)