Представление полиномов общего вида ,

a_ks –коэффициент полинома, который определяется по известным точкам, k+s=n – степень полинома (число членов),

x,y – координаты точек.

Для каждой определяемой точки составляется уравнение, где x, y и z_xy известны. По ряду точек находится коэффициент a_ks. Если число точек больше n , то коэффициенты находятся под условием минимума суммы наименьших квадратов.

Если число членов равно числу точек, то определитель системы обращается в ноль в следующих случаях:

• при n=2, если три точки лежат на одной прямой;

• при n=5, если шесть точек лежат на одной кривой второго порядка;

• при n=9, если десять точек лежат на одной кривой третьего порядка.

То есть узлы не могут быть расположены произвольно.

Аппроксимация поверхности ортогональными полиномами Чебышёва.

Дана регулярная сетка квадратов, в узлах которой находятся известные точки. Аппроксимирующий полином выражается в виде линейной комбинации ортогональных полиномов Чебышёва:

F(x,y) = a₀₀₀(x) ₀(y) a₀₁₀(x) ₁(y) a₁₀₁(x) ₀(y) a₀₂₀(x)₂(y) a_kl_k(x) _l(y),

где ₀(x), ₀(y), ₁(x), ₁(y),, _k(x) _l(y) – заданная система полиномов, удовлетворяющая условию ортогональности

при kl. Коэффициенты a_kl находятся из выражения .

Преимущество ортогональных полиномов перед степенными в том, что:

а) все решения выполняются согласно теории наименьших квадратов без сопутствующих построений вычислений;

б) при переходе к более высокой степени коэффициенты a_kl не меняются. Вычисляются только соответствующие старшие члены.

При равноотстоящих точках (регулярная матрица высот) ортогональные полиномы легче вычислять, но в этом случае накладываются ограничения на порядок расположения точек на регулярной сетке.

Построение сглаживающей кривой с помощью сплайнов

Сплайном ( сплайн = лекало) называют гладко-кусочную кривую, состоящую из гладко сопряженных полиномов. Широко используются кубические полиномы. Для кубического сплайна в точках узлов первая и вторая производные должны быть непрерывны, чтобы кривая гладко переходила в другую кривую.

Имеем: (x) – полином степени меньшей или равной трём на отрезке [x_i-1 , x_i]; (x_i) = z_i; и ’(x) и ”(x) непрерывны в точках.

Берём первый отрезок [x₀ , x₁], известно, что (x₀) = z₀ и (x₁) = z₁. Зададим: ’(x₀) = z₀’ и ”(x₁) = z₁”. Для следующего отрезка [x₁ , x₂] имеем (x₁) = z₁ и (x₂) = z₂, вычисляем ’(x) и ”(x) по первому сплайну, строим кубическую функцию на отрезке [x₁ , x₂] и так далее.

Другими словами для построения данной кривой необходимо n+1 точка и два начальных условия. Для повышения точности можно задавать по одной производной на каждом конце сплайна. Этот приём аппроксимации широко применяется и включён практически во все программы обрисовки гладких кривых по ЦМВ.

Сглаживание данных сплайн – функциями

Построение гладкой кривой для функции, построенной по экспериментальным данным (x_i , y_i) i =1,..n; x_i+1 > x_i , с помощью сплайн-функции, которая на интервале (x_i , x_i+1) имеет вид:

,

где n-число точек, m- число, отражающее степень (2m-1) сглаживающего сплайна. Сглаживание идет под условием минимума функционала , при условии, гдеq^(m) - производная порядка m функции q(x) , S - выбирается в интервале .

Это условие преобразуется к виду: . Задача минимизации решается методом Лагранжа, т.е. нахождениемабсолютного? минимума функции

Для определения коррелаты P в процедуре метода Ньютона решается нелинейное уравнение. После этого задача сводится к нахождению из системы линейных уравнений, решением по методу Гаусса.

B-spline

B-spline (фундаментальный сплайн) четвёртого порядка (третьей степени 0 1 2 3) из различных видов сплайнов используется наиболее широко. Он имеет минимальный носитель, то есть число отрезков, на которых он отличен от нуля. Полиномиальный сплайн отличен от нуля только на четырёх отрезках. Поэтому, если у нас есть этот сплайн, то во всех точках, кроме данных он тождественно равен нулю.

Любой сплайн порядка m может быть выражен через линейную комбинацию В-сплайнов:,

где -В-сплайн порядка m (степени m-1), c_i – числовой коэффициент.

Интерполирование по регулярной сетке.

Интерполяции я

Линейная. Если дана плотная сеть точек, то применяют линейную интерполяцию. ,где необходимый минимум - три точки. Лучшее качество аппроксимации выполняется при повышении степени полинома, и соответственно применении большего числа точек, но при этом удлиняется процесс решения, возникают искажения.

Квадратичная. Применяют уравнение второй степени: , для его реализации необходимо не меньше шести точек.

Билинейная: ,l – сторона сетки.

Бикубическая: 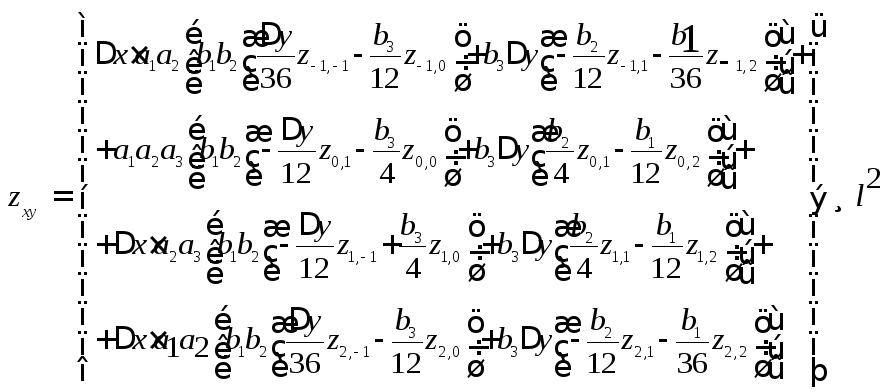, где