
курс лекций ТММ / курс лекций ТММ / Лекции3 и4 тмм
.docxЛекция №3
Кинематический анализ плоских механизмов.
Целью кинематического анализа является определение перемещений,
скоростей и ускорений звеньев или каких-то их точек при заданных размерах и движении ведущего звена.
. Расчёт может быть осуществлён аналитическим или графо-аналитическим методами. Последний метод менее точен, но проще и менее трудоёмок, благодаря чему часто применяется на практике, когда обеспечивает требуемую точность.
При их использовании необходимо по заданным размерам вычертить в масштабе схему механизма в заданном положении (рис.3.1). В данном курсе методика кинематического, силового и динамического расчёта используется для случая кривошипно- ползунного механизма Рассматривается наиболее распространенная схема центрального механизма, в котором линия движения точки В ползуна проходит через центр вращения кривошипа (используется в двигателях внутреннего сгорания). Механизм имеет одну степень свободы: положение всех его подвижных звеньев можно задать с помощью одного независимого параметра (например, угла поворота кривошипа).
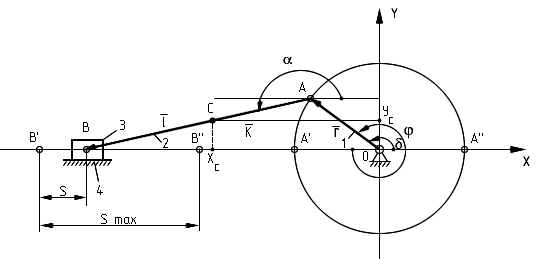
Рис.3.1
Аналитическое определение перемещений, аналогов скоростей и ускорений.
Введем
в рассмотрение правую систему координат
X,
Y
с центром в точке O.
Ось X
параллельна линии движения ползуна.
Считаем известными размеры кривошипа
OA= ,
шатуна AB=
,
шатуна AB=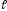 .
Направление вращения кривошипа принимаем
против часовой стрелки. За один оборот
кривошипа ползун перемещается между
двумя крайними положениями B'
и B''
на величину Smax=
.
Направление вращения кривошипа принимаем
против часовой стрелки. За один оборот
кривошипа ползун перемещается между
двумя крайними положениями B'
и B''
на величину Smax= .
Величину перемещения S
отсчитываем от крайнего левого положения
ползуна B'
, а величину угла
.
Величину перемещения S
отсчитываем от крайнего левого положения
ползуна B'
, а величину угла
 от соответствующего положения кривошипа
(OA').
от соответствующего положения кривошипа
(OA').
Введем в рассмотрение замкнутый векторный контур OABO. В любом положении механизма выполняется условие:
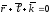 .
(3.1)
Углы, составленные данными векторами
с положительным направлением оси X
и отсчитываемые против часовой стрелки,
соответственно равны ,
,
0. Спроектируем векторное уравнение
(3.1) на оси X,
Y:
.
(3.1)
Углы, составленные данными векторами
с положительным направлением оси X
и отсчитываемые против часовой стрелки,
соответственно равны ,
,
0. Спроектируем векторное уравнение
(3.1) на оси X,
Y:
 ,
(3.2)
,
(3.2)
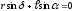 .
(3.3)
.
(3.3)
Учитывая,
что
 и
и
 ,
после преобразований получаем из
уравнений (3.2) и (3.3) функции
положения шатуна и ползуна
;
,
после преобразований получаем из
уравнений (3.2) и (3.3) функции
положения шатуна и ползуна
;
угол
поворота шатуна
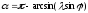 (3.4) перемещение
ползуна
(3.4) перемещение
ползуна
 .
(3.5) Здесь
.
(3.5) Здесь
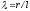 .
.
Определим
координаты произвольной точки С шатуна.
Ее положение задается расстоянием
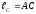 .
В векторной форме
.
В векторной форме
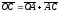 .
В проекциях на оси X,
Y
получаем функции
положения точки С.
.
В проекциях на оси X,
Y
получаем функции
положения точки С.
 ,
(3.6)
,
(3.6)
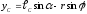 .
.
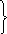
Первая
и вторая производные от функции положения
по углу
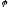 называются аналогами
скоростей и ускорений.
называются аналогами
скоростей и ускорений.
Найдем зависимости для вычисления аналогов скоростей и ускорений звеньев и точек механизма.
Дифференцируя
дважды уравнение (3.4) по
 ,
получим выражения для аналогов угловой
скорости и углового ускорения шатуна
,
получим выражения для аналогов угловой
скорости и углового ускорения шатуна
 ; (3.7)
; (3.7)
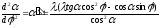 .
(3.8)
.
(3.8)
Дифференцируя
дважды уравнение (3.5) по
 ,
получим зависимости для нахождения
аналогов
скоростей и ускорений ползуна
:
,
получим зависимости для нахождения
аналогов
скоростей и ускорений ползуна
:
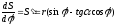 (3.9)
(3.9)
 .
(3.10)
.
(3.10)
Дифференцируя
дважды уравнения (3.6) по
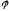 ,
получим в проекциях на оси X,Y
выражения аналогов
скорости и ускорения произвольной точки
С шатуна:
,
получим в проекциях на оси X,Y
выражения аналогов
скорости и ускорения произвольной точки
С шатуна:
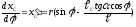 ;
;
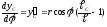 ;
(3.11
;
(3.11
 );
(3.12)
);
(3.12)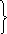
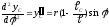 .
.
При
значениях
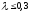 для определения перемещения, аналогов
скорости и ускорения ползуна можно
использовать приближенные завис
для определения перемещения, аналогов
скорости и ускорения ползуна можно
использовать приближенные завис
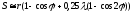 .
(3.13)
.
(3.13)
 .
(3.14) .
.
(3.14) .
 (3.15)
(3.15)
Для
наглядного представления о характере
изменения геометрических и кинематических
параметров механизма строятся
кинематические диаграммы.
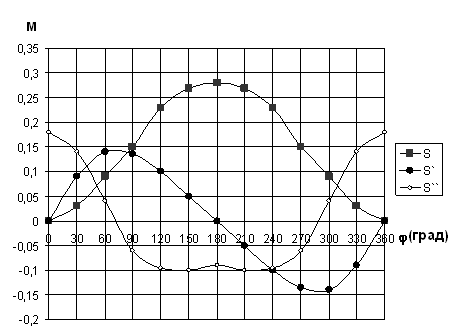
Рис.3.2
При построении необходимо учитывать взаимосвязь между ними, выражающуюся в согласованном расположении характерных точек. Нулевому значению аналога скорости соответствует максимальное (или минимальное) значение перемещения ползуна. Нулевым значениям аналога ускорения соответствуют точки максимума или минимума на графике аналога скорости и точки перегиба на графике перемещения. Точкам максимума или минимума на графике аналога ускорения соответствуют точки перегиба на графике аналога скорости.
Определение скоростей и ускорений звеньев и их точек
Скорости
и ускорения звеньев и их точек определяются
при заданной угловой скорости
 и угловом ускорении
и угловом ускорении
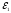 ведущего звена (кривошипа). Для нахождения
скоростей звеньев необходимо
продифференцировать их перемещения по
времени t
в соответствии с правилами дифференцирования
сложных функций.
ведущего звена (кривошипа). Для нахождения
скоростей звеньев необходимо
продифференцировать их перемещения по
времени t
в соответствии с правилами дифференцирования
сложных функций.
Угловая
скорость шатуна:
 .
(3.16)
.
(3.16)
Аналог
углового ускорения шатуна
 определяется по зависимости (3.7).
определяется по зависимости (3.7).
Линейная
скорость ползуна .
 (3.17)
(3.17)
Аналог
скорости ползуна
 находится по зависимости (3.9) или (3.14).
находится по зависимости (3.9) или (3.14).
Линейная скорость точки С шатуна в проекциях на оси X,Y
 ;
;
 .
(3.18)
.
(3.18)
Величины
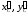 определяются по зависимостям (3.11).
определяются по зависимостям (3.11).
Модуль
вектора скорости
 .
(3.19)
.
(3.19)
Угловое
ускорение шатуна
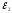 найдем дифференцированием по времени
t
выражения (3.16):
найдем дифференцированием по времени
t
выражения (3.16):
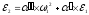 .
(3.20)
Величина аналога углового
ускорения шатуна
.
(3.20)
Величина аналога углового
ускорения шатуна
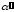 определяется по
определяется по
зависимости (3.8).
Линейное
ускорение ползуна
 найдем дифференцированием по времени
t
зависимости (3.17)
найдем дифференцированием по времени
t
зависимости (3.17)
 .
(3.21)
.
(3.21)
Аналог
ускорения ползуна определяется по зависимости (3.10) или
(3.15).
определяется по зависимости (3.10) или
(3.15).
Линейное
ускорение точки С шатуна в проекциях
на оси X,
Y
находим дифференцированием по времени
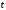 зависимостей (3.18):
зависимостей (3.18):
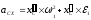 ;
;
 .
(3.22)
.
(3.22)
Величины
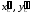 находятся по зависимости (3.12).
находятся по зависимости (3.12).
Модуль
вектора ускорения точки С
 .
(3.23)
.
(3.23)
Лекция № 4
Определение скоростей и ускорений плоских рычажных механизмов методом планов
Данный метод позволяет вычислить величины скоростей и ускорений без использования аналитических зависимостей. Подробное изложение данного метода приведено в работах [1], [2]. Построение планов скоростей и ускорений выполним для кривошипно –ползунного механизма в положении , показанном на рис. 4.1.
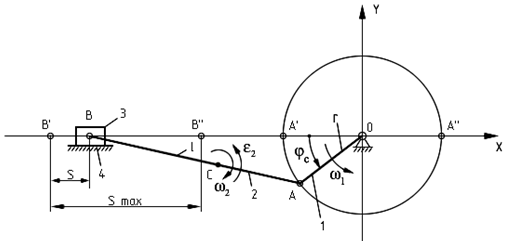
Рис.4.1
Скорость
точки А, принадлежащей звеньям 1 и 2,
определим как окружную во вращательном
движении:
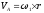 .
Вектор
.
Вектор
 направлен перпендикулярно ОА в сторону
направлен перпендикулярно ОА в сторону
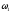 .
Для определения скорости точки В,
принадлежащей звеньям 2 и 3, разложим
движение звена 2 на переносное
поступательное вместе с точкой А и
относительное вращательное вокруг
точки А. Тогда имеем
.
Для определения скорости точки В,
принадлежащей звеньям 2 и 3, разложим
движение звена 2 на переносное
поступательное вместе с точкой А и
относительное вращательное вокруг
точки А. Тогда имеем
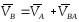 .
(4.1)
.
(4.1)
В
данном уравнении вектор
 известен, линия действия
известен, линия действия
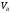 совпадает с линией движения ползуна,
линия действия относительной скорости
совпадает с линией движения ползуна,
линия действия относительной скорости
 перпендикулярна линии АВ шатуна.
перпендикулярна линии АВ шатуна.
Решение этого векторного уравнения производим графически путем построения плана скоростей (рис.4.2).
Из
полюса р проводим отрезок р произвольной длины, изображающий вектор
произвольной длины, изображающий вектор
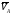 .
Масштаб плана скоростей
.
Масштаб плана скоростей
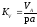 .
Рекомендуется при построении принимать
.
Рекомендуется при построении принимать
 .
Далее из полюса
.
Далее из полюса
 проводим линию действия скорости
проводим линию действия скорости
 параллельно линии хода ползуна, а через
точку
параллельно линии хода ползуна, а через
точку
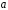 - линию действия
- линию действия
 перпендикулярно АВ. Точка
перпендикулярно АВ. Точка
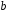 пересечения двух линий определяет
величины векторов.
пересечения двух линий определяет
величины векторов.
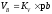 ;
;
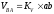 .
.
Направление
векторов
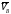 и
и
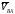 определяется по уравнению (4.1).
определяется по уравнению (4.1).
Угловая
скорость шатуна
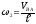 .
Её направление определяется по направлению
скорости
.
Её направление определяется по направлению
скорости
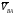 ,
приложенной в точке В.
,
приложенной в точке В.
Для
нахождения вектора скорости точки С
шатуна воспользуемся изображающими
свойствами плана скоростей [1]. В
соответствии с ними три точки одного
звена на схеме механизма и три
соответствующие точки на плане скоростей
образуют подобные и сходственно
расположенные фигуры. В данном случае
три точки А, В, С шатуна находятся на
одной линии. Следовательно, изображающая
точка С на плане скоростей будет
расположена между точками
 и
и
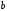 .
Её положение определится из соотношения:
.
Её положение определится из соотношения:
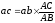 .
Вектор
.
Вектор
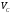 проводим из полюса
проводим из полюса
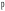 в точку С.
в точку С.
 .
.
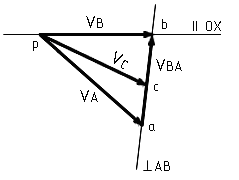 Рис.4.2
Рис.4.2
Построение плана ускорений выполним для того же положения механизма (рис.4.1).
Ускорение
точки А складывается из двух составляющих:
центростремительного и вращательного.
 .
.
Для
упрощения задачи будем считать угловую
скорость кривошипа
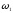 постоянной. Тогда угловое ускорение
кривошипа
постоянной. Тогда угловое ускорение
кривошипа
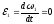 ,
и
,
и
 .
Следовательно,
.
Следовательно,
 .
.
Вектор
 направлен параллельно ОА к центру
вращения.
направлен параллельно ОА к центру
вращения.
Определение ускорения точки В производится на основании разложения движения звена 2 на переносное поступательное с точкой А и относительное вращательное вокруг этой точки.
В
соответствии с этим ускорение точки В
определится из векторного уравнения

Так
как относительное движение - вращательное:
 .
.
Тогда
:
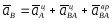 .
(4.2)
.
(4.2)
Следует заметить, что кориолисово ускорение в данном случае равно 0, так как переносное движение поступательное.
Центростремительное
ускорение
 направлено параллельно шатуну от точки
В к точке А.
направлено параллельно шатуну от точки
В к точке А.
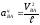 .
.
Вращательное
ускорение
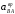 перпендикулярно
перпендикулярно
 .
Линия действия
.
Линия действия
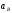 совпадает с линией движения ползуна.
Решение уравнения (4.2) проводим графически
путем построения плана ускорений (рис.
4.3).
совпадает с линией движения ползуна.
Решение уравнения (4.2) проводим графически
путем построения плана ускорений (рис.
4.3).
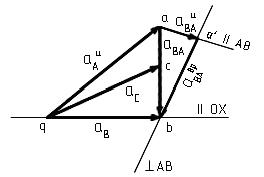
Рис.4.3
Из
полюса
 проводим отрезок
проводим отрезок
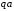 произвольной длины, изображающий вектор
произвольной длины, изображающий вектор
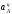 .
Масштаб плана ускорений
.
Масштаб плана ускорений
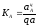 .
Рекомендуется при построении принимать
.
Рекомендуется при построении принимать
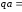 100мм.
Далее, из точки
100мм.
Далее, из точки
 откладываем
откладываем
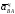 в виде отрезка
в виде отрезка
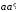 параллельно АВ в направлении от точки
В к точке А.
параллельно АВ в направлении от точки
В к точке А.
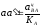
Из
точки
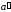 проводим линию действия
проводим линию действия
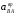 перпендикулярно шатуну АВ, а из полюса
перпендикулярно шатуну АВ, а из полюса
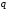 линию действия
линию действия
 параллельно линии хода ползуна.
параллельно линии хода ползуна.
Точка
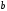 пересечения этих линий определяет
величины ускорений.
пересечения этих линий определяет
величины ускорений.
 ,
,
 .
.
Направление
векторов
 и
и
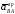 определяются по уравнению (4.2).
определяются по уравнению (4.2).
Угловое
ускорение шатуна
 .
Его направление определяется по
направлению ускорения
.
Его направление определяется по
направлению ускорения
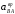 ,
приложенному в точке В.
,
приложенному в точке В.
Для
нахождения вектора ускорения точки С
шатуна воспользуемся изображающими
свойствами плана ускорений, которые
аналогичны свойствам плана скоростей
[2]. Изображающая точка С на плане ускорений
будет находиться между точками
 и
и
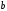 .
Её положение определится из соотношения:
.
Её положение определится из соотношения:
 .
.
Вектор
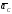 проводим из полюса
проводим из полюса
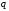 в точку С.
в точку С.
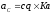 .
.
