Зубчатые механизмы

В технике различают трёхзвенные зубчатые передачи, многоступенчатые передачи и планетарные передачи. Трёхзвенная передача состоит из двух зубчатых колёс и стойки.

Передача, в которой угловая скорость ведомого звена меньше, чем угловая скорость ведущего звена, называется понижающей передачей (редуктор). Если в зубчатой передаче происходит увеличение угловой скорости ведомого звена, передача называется повышающей (мультипликатор).

На рис.2.9 приводятся условные изображения трёхзвенной цилиндрической зубчатой передачи внешнего зацепления (рис.2.9, а), цилиндрической передачи внутреннего зацепления (рис.2.9, б) и реечной зубчатой передачи (рис.2.9,в ).

На условных изображениях плоских и пространственных зубчатых пар колёса на виде с торца изображают штрихпунктирными линиями. Зубья изображают только на зубчатой рейке. На виде сбоку зубчатые колёса изображают сплошными линиями.

Рис.2.9

В некоторых случаях на кинематической схеме требуется различать прямозубые и косозубые колёса. Соответствующие условные обозначения представлены на рис.2.10, а и 2.10, б.

Для различения колёс, вращающихся на оси и закреплённых на валу, применяют условные обозначения колёс по рис.2.10, в и 2.10, г.

Рис. 2.10

На рис.2.11 показано в двух проекциях условное изображение конической зубчатой передачи, которая передаёт вращение между пересекающимися осями.

Рис.2.11

На рис.2.12 приводятся условные изображения червячной передачи с цилиндрическим червяком (рис.2.12, а) и винтовой зубчатой передачи (рис.2.12,б).

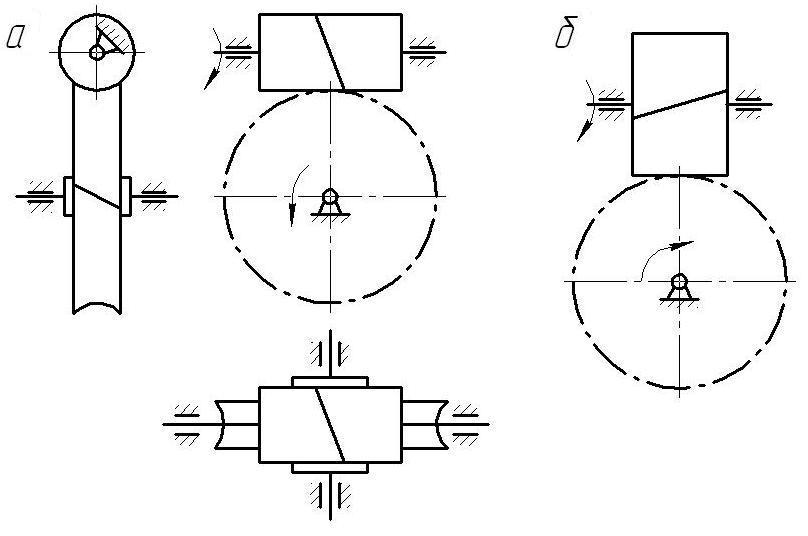
Рис.2.12

Оси колёс в этих передачах перекрещиваются. Червячная передача применяется для передачи вращения от червяка к червячному колесу в качестве понижающей передачи. При зацеплении зубья червяка и колеса находятся в линейном контакте. Винтовая зубчатая передача состоит из двух косозубых (винтовых) колёс. Ввиду того, что зубья в винтовой передаче касаются в точке, её нагрузочная способность ниже, чем нагрузочная способность червячной передачи.

На кинематических схемах червячных и винтовых передач должно быть задано направление винтовой линии червяка в червячной передаче и направление винтовой линии одного из зубчатых колёс винтовой зубчатой передачи. Различают правые и левые винтовые линии.

Для определения направления винтовой линии следует мысленно перемещаться по образующей цилиндрической заготовке червяка или косозубого колеса, начиная движение от любого из двух его торцов, до встречи с винтовой линией и, рассматривая винтовую линию как препятствие, продолжать движение по винтовой линии. Если при этом потребуется повернуть направо, винтовая линия называется правой, при повороте налево-левой винтовой линией. На кинематических схемах по рис.2.12 червяк и косозубое колесо винтовой передачи представляют собой соответственно правый червяк и левое косозубое колесо.

На рис.2.13 представлены условные изображения двух наиболее часто применяемых планетарных механизмов: плоской планетарной передачи (рис.2.13, а) и конической планетарной передачи (рис.2.13, б). Планетарными называются механизмы, которые имеют зубчатые колёса, оси которых вращаются в пространстве. Планетарные механизмы с одной степенью свободы (с одним двигателем) называются планетарными передачами.

Зубчатые колеса а и в планетарных передач называются центральными. Колесо в в рассматриваемых схемах представляет собой неподвижное колесо. Колесо с с подвижной осью вращения называется планетарным (сателлит). Звено h называется водило.

В планетарных механизмах, представленных на рис.2.13, передача движения возможна от колеса а к водилу h и наоборот.

Рис.2.13

ВИНТОВЫЕ МЕХАНИЗМЫ

Простейший винтовой механизм (рис.2.14) состоит из винта 1, гайки 2 и стойки 3. Гайка является одновременно ползуном, который перемещается поступательно в неподвижных направляющих. Этот механизм называют также передачей ''винт-гайка''.

Рис.2.14

СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ.

Числом степеней свободы механизма называется число независимых геометрических параметров, однозначно определяющих положение всех его подвижных звеньев в пространстве.

Для определения числа степеней свободы пространственного механизма можно использовать формулу Малышева:

W = 6(n-1) - 5p₁ - 4p₂ - 3p₃ - 2p₄ - p₅ . (2.1)

Здесь: n - число звеньев механизма, включая неподвижное.

Тогда 6(n-1) - общее число степеней свободы подвижных звеньев до соединения их в кинематические пары.

Соединение звеньев в кинематические пары накладывает связи на относительное движение звеньев и ограничивает их подвижность.

Например, каждая одноподвижная пара (рис.1.1), (рис.1.2) отнимает у механизма пять степеней свободы, пятиподвижная пара (рис.1.9) отнимает одну степень свободы. Соответственно:

р₁ – число одноподвижных кинематических пар;

р₂ – число двухподвижных кинематических пар; и так далее…

р₅- число пятиподвижных кинематических пар.

Примеры наиболее распространённых пар приведены на рис.1.1- рис.1.9.

Для плоских механизмов, звенья которых двигаются в параллельных плоскостях, используется формула Чебышева:

W = 3(n-1) - 2p₁ - p₂ . (2.2)

Если при расчёте по формулам (2.1) или (2.2) получается w ≤ 0, это означает, что данная конструкция не механизм, а статически определимая или неопределимая ферма.

Большинство механизмов, используемых в технике, имеют одну степень свободы, то есть приводятся в движение одним двигателем. Механизмы с двумя степенями называются дифференциальными. Механизмы роботов и манипуляторов имеют четыре и более степеней свободы. Вариант такого механизма показан на рис.2.15.

Рис.2.15

Формулы (2.1) и (2.2) получены из предположения, что все связи, наложенные на механизм, независимы.

В некоторых механизмах эти условия не выполняются. В общее число наложенных связей может войти q избыточных (пассивных) связей, которые не уменьшают подвижностей механизма. По формулам получается w.≤.0, но механизм (при определённых условиях) является работоспособным.

В качестве примера можно рассмотреть широко распространённый плоский кривошипно-ползунный механизм (рис.2.1). В нём все четыре кинематические пары являются одноподвижными. При расчёте по формуле Чебышева (2.2) W = 3 ∙ 3 – 2 ∙ 4 = 1.

Если тот же механизм рассматривать как пространственный, то по формуле Малышева (2.1) W = 6 ∙ 3 – 5 ∙ 4 = -2. !!!

Т.е. в плоском работающем механизме имеются три избыточных (пассивных) связи. Их появление объясняется там, что оси шарниров А, О, В строго параллельны между собой и перпендикулярны плоскости движения ползуна. Если эти условия не выполняются, то работа механизма возможна лишь при изменении подвижностей кинематических пар. Например, если шарнир В заменить на сферический (рис.1.6), а шарнир А на пространственный (рис.1.5), тогда по формуле Малышева (2.1) W = 6 ∙ 3 – 5 ∙ 2 – 4 ∙ 1 – 3 ∙ 1 = 1.

Такое устранение избыточных связей снижает требования к точности изготовления и монтажа звеньев. Однако при этом происходит усложнение конструкции и снижение жёсткости системы.

В ряде случаев избыточные связи вводят специально для повышения жёсткости механизма или устранения неопределённости движения звеньев в некоторых его положениях. Примером может служить плоский механизм сдвоенного параллелограмма (рис.2.16).

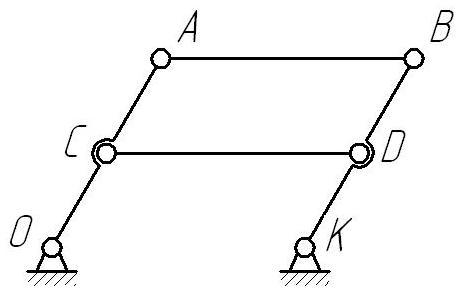
Рис.2.16

При расчёте по формуле (2.2) W = 3 ∙ 4 – 2 ∙ 6 = 0.

А фактически механизм имеет одну степень свободы. Для этого необходимо строгое соблюдение геометрических соотношений:

АВ = СD = ОК, ОА = ВК, AС = ВD и высокой точности изготовления механизма. При этом дополнительное звено СD не вносит новых геометрических связей. Оно введено для увеличения жёсткости механизма и не даёт возможности во время его работы превращаться из механизма параллелограмма в антипараллелограмм.

В некоторых случаях в механизм вводят лишние (пассивные) степени подвижности. Примером может быть установка ролика между толкателем и кулачком для уменьшения износа в кинематической паре (рис.2.7, а). При расчёте по формуле Чебышева (2.2) для плоского механизма: n = 4, р₁ = 3, р₂ = 1

В этом случае W = 3 ∙ 3 – 2 ∙ 3 – 1 = 2 , однако, вторая степень свободы является пассивной (вращение круглого цилиндрического ролика вокруг своей оси).

Этот же механизм может служить примером устранения избыточных связей. Если его рассматривать как пространственный, то при предполагаемом линейном контакте ролика с толкателем по формуле Малышева (2.1) : n = 4,

р₁ = 3, р₃ = 1. W = 6 ∙ 3 – 5 ∙ 3 – 3 ∙ 1 = 0. Это означает, что из-за неточностей изготовления (непараллельность осей ролика и кулачка) линейный контакт цилиндрических поверхностей ролика и кулачка может превратиться в кромочный. Нормальная работа механизма при этом нарушается. Устранить это можно путём применения бочкообразного ролика (рис.2.17), имеющего точечный контакт с кулачком.

Рис.2.17

Тогда получаем при n = 4, р₁ = 3, р₅ = 1, W = 6 ∙3 – 5 ∙ 3 – 1 = 2, т. е. формула даёт тот же результат, что и для плоского механизма. Однако при этом следует учитывать, что точечный контакт ролика и кулачка, снижая требования к точности изготовления и монтажа, одновременно уменьшает величину передаваемых нагрузок.