
курс лекций ТММ / курс лекций ТММ / сил.ан. лекц 5,6
.docxЛекция №5
Силовой анализ плоских рычажных механизмов
Целью силового расчета механизма является определение реакций в кинематических парах, усилий, приложенных к звеньям, ориентировочной мощности двигателя. Результаты могут быть использованы при проектировочных расчетах деталей и узлов механизма.
Силы, действующие в механизме.
-
Внешние силы.
а) Силы и моменты полезного сопротивления. Направлены против движения звена, к которому они приложены. При проектировании должны быть заданы в виде графиков или диаграмм.
б) Движущие силы или моменты. Совпадают с направлением
движения звена, к которому они приложены. Определяются в процессе силового анализа.
в) Силы тяжести подвижных звеньев.
2. Внутренние силы.
а) Реакции в кинематических парах.
Их величина и направление определяются при силовом расчёте.
В плоских механизмах, в основном, используются низшие поступательные и вращательные кинематические пары (рис1.1 и.1.2).
В поступательной паре линия действия реакции перпендикулярна линии относительной скорости перемещения звеньев.
Во вращательной паре линия действия реакции неизвестна. Поэтому приходится её раскладывать на два направления (обычно вдоль задаваемых осей координат.
В плоской кулачковой паре с точечным контактом звеньев (рис.1.4) реакция всегда направлена по нормали в точке контакта.
б) Силы трения в кинематических парах.
В первую очередь это силы трения скольжения.
Трение является сложным физико-химическим процессом, сопровождающимся выделением тепла. Это вызвано тем, что перемещающиеся тела оказывают сопротивление относительному движению. Мерой интенсивности сопротивления относительному перемещению является сила (момент) трения.
Различают трение качения, трение скольжения, а также сухое, граничное и жидкостное трение.
Если суммарная высота микронеровностей взаимодействующих поверхностей:
-
больше, чем высота слоя смазки, то - сухое трение.
-
равна высоте слоя смазки, то - граничное трение.
-
меньше, чем высота слоя смазки, то - жидкостное .
Учет трения скольжения в поступательной кинематической паре.
Без учета
трения реакция направлена по нормали
к взаимодействующим поверхностям. При
учете трения результирующая реакция
Q21
отклоняется от общей нормали на угол
трения
в сторону противоположную направлению
движения.
без учета трения с учетом трения
Fтр=Qn12.tg

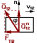
tg = f
Fтр=Qn12.f
Рис.5.1
Коэффициент трения f определяется экспериментально и зависит от:
а) чистоты обработки контактирующих поверхностей;
б) наличия и характера смазки;
в) сочетания трущихся материалов или вида покрытия деталей.
Учет сил трения скольжения во вращательной кинематической паре.


1 - цапфа
rц - радиус цапфы
Δ - зазор
- радиус круга трения;
= О1С
Рис.5.2
Из
ΔО1СК
 =
sin
О1С
= О1К
sin
=
sin
О1С
= О1К
sin
Mc= Q12.О1С = Q12. rц.sin
При малых углах sin ≈ tg = f .
Тогда :
Mc= Q12. rц.f
При учете трения во вращательной КП результирующая реакция отклоняется
от общей нормали на угол трения и проходит касательно к кругу трения радиуса .
Трение качения- трение движения двух твёрдых тел , при котором их скорости в точках касания одинаковы по величине и направлению.
Вследствие контактных деформаций трение качения сопровождается неизбежным скольжением и рассеянием энергии в результате внутреннего трения.
Для расчёта силы трения используется формула Кулона. При качении цилиндра (сферы) по плоскости ( рис.5.3)
Ff= k*Fn/R , где k- коэффициент трения качения;
Fn- cила, с которой цилиндр прижат к плоскости;
R – радиус цилиндра (сферы).
Коэффициент трения качения ( мм.) - берётся из справочников и зависит от твёрдости контактирующих поверхностей.

Рис.5.3
Методика силового расчета рычажного механизма.
Рассмотрим
аналитический метод силового анализа
на примере схемы кривошипно-ползунного
механизма (рис.5.4). Здесь же показаны все
приложенные силы и моменты. При силовом
расчете должны быть заданы (в метрах):
радиус кривошипа
 ,
длина шатуна
,
длина шатуна
 .
Положение центров масс звеньев
определяется расстояниями
.
Положение центров масс звеньев
определяется расстояниями
 ,
,
 ,
,
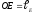 .
.
Задается
средняя угловая скорость кривошипа
 .
.
Считаются
известными: масса кривошипа
 (кг), масса шатуна
(кг), масса шатуна
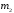 (кг),
(кг),
масса
ползуна
 (кг), масса противовеса
(кг), масса противовеса
 (кг), момент инерции шатуна относительно
центра массы
(кг), момент инерции шатуна относительно
центра массы
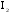 (кгм2).момент
инерции вращающихся масс на валу
кривошипа
(кгм2).момент
инерции вращающихся масс на валу
кривошипа
 (кгм2).
(кгм2).
Положение
механизма на плоскости определяется
углом
 между положительным направлением оси
Х и вектором силы тяжести (отсчитывается
от оси Х против часовой стрелки).
между положительным направлением оси
Х и вектором силы тяжести (отсчитывается
от оси Х против часовой стрелки).
Угол
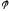 отсчитывается от положения кривошипа
отсчитывается от положения кривошипа
 ,
в котором ползун занимает крайнее
дальнее положение
,
в котором ползун занимает крайнее
дальнее положение
 .
.
Во
всех положениях механизма задается
величина углового ускорения кривошипа
 (с-2).
Его величина определяется в результате
динамического анализа машины .
(с-2).
Его величина определяется в результате
динамического анализа машины .
Отсчет
угла
 ,
направление угловой скорости
,
направление угловой скорости
 и углового ускорения
и углового ускорения
 против часовой стрелки считаются
положительными.
против часовой стрелки считаются
положительными.

Рис.5.4
К ползуну приложена внешняя сила P (Н). Её величина задается в каждом положении механизма и является положительной, если ее направление совпадает с осью Х.
Силы трения в кинематических парах не учитываются.
На
кривошипе должен быть приложен
уравновешивающий момент
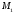 (Нм), величина и направление которого
определяются в каждом положении.
(Нм), величина и направление которого
определяются в каждом положении.
Определяются силы тяжести звеньев:
 (5.1)
(5.1)
где g=9,8 м/с2 .
Исследование ведется по методу кинетостатики [1]. К движущемуся механизму применяются уравнения равновесия статики, но в рассмотрение вводятся инерционные нагрузки (принцип Даламбера) .
Силы инерции звеньев:
 ;
;
 .
(5.2)
.
(5.2)
Здесь
и далее не учитываются касательные
составляющие сил инерции
 и
и
 ,
возникающие при движении кривошипа с
ускорением.
,
возникающие при движении кривошипа с
ускорением.
Инерционные моменты кривошипа и шатуна:
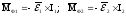 .
(5.3)
.
(5.3)
Величины
ускорений центров масс звеньев
 величины угловых ускорений кривошипа
величины угловых ускорений кривошипа
 ,
шатуна
,
шатуна
 определяются при кинематическом и
динамическом анализе хода машины.
определяются при кинематическом и
динамическом анализе хода машины.
Для нахождения реакций в кинематических парах нужно выделить из механизма статически определимую группу звеньев, в которой число неизвестных реакций равно числу уравнений кинетостатики (три уравнения).
Например, в начале расчётов нельзя рассматривать равновесие шатуна 2, так как в шарнирах А и В неизвестны по величине и направлению реакции со стороны кривошипа R12 и ползуна R32.
В данном случае, рассматриваем равновесие статически определимой структурной группы “шатун-ползун” (рис.5.5).

Рис.5.5
Векторное уравнение равновесия сил:
 .
(5.4)
.
(5.4)
Здесь
 и
и
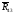 —
реакции со стороны “отброшенных”
звеньев 1 и 4 соответственно на звенья
2 и 3. При этом считаем, что положительное
направление
—
реакции со стороны “отброшенных”
звеньев 1 и 4 соответственно на звенья
2 и 3. При этом считаем, что положительное
направление
 совпадает с осью Y.
совпадает с осью Y.
Проектируя уравнения (5.4) на ось X и используя при этом зависимости (5.1), (5.2),получим:
 .
(5.5)
.
(5.5)
Здесь
 определяются по зависимостям (3.22) и
(3.21).
определяются по зависимостям (3.22) и
(3.21).
Уравнение равновесия моментов всех сил относительно, например, точки A:
 .
(5.6)
.
(5.6)
Это уравнение, выраженное через проекции векторов на оси координат X,Y, имеет вид:

Величины
 определяются по зависимостям (3.6).
Координаты
определяются по зависимостям (3.6).
Координаты
 и
и
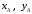 можно вычислить по тем же зависимостям
(3.6), подставляя вместо
можно вычислить по тем же зависимостям
(3.6), подставляя вместо
 соответственно
соответственно
 и
и
 .
.
Используя зависимости (5.1), (5.2), (5.3), после преобразований получаем:
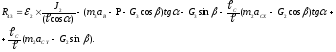
(5.7)
Проектируя уравнение (5.4) на ось Y системы координат и используя при этом зависимости (5.1), (5.2), получим:
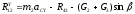 .
(5.8)
.
(5.8)
Определим
реакцию
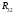 в шарнире
в шарнире
 .
Условие равновесия шатуна запишется в
виде:
.
Условие равновесия шатуна запишется в
виде:

Проектируя данное векторное уравнение на оси X,Y, получим:

 ,
(5.8)
,
(5.8)
 .
.
Для
определения реакции
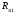 в шарнире О и величины уравновешивающего
момента
в шарнире О и величины уравновешивающего
момента
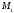 рассмотрим равновесие кривошипа 1
(рис.5.6)
рассмотрим равновесие кривошипа 1
(рис.5.6)

Рис.5.6
Векторное уравнение равновесия сил на кривошипе:
 (5.9)
(5.9)
Проектируя
уравнение (5.9) на оси X,Y
системы координат с использованием
зависимостей (5.1), (5.2) и учитывая, что
 ,
получаем:
,
получаем:
 ,
(5.10)
,
(5.10)
 .
.
Так как точки А, Е, D кривошипа находятся на одной линии, проекции центростремительных ускорений определяются по формулам:
 ;
;
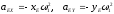 ,
(5.11) где,
,
(5.11) где,
 ;
;
 .
(5.12)
.
(5.12)
Уравнение равновесия моментов всех сил относительно точки О, выраженное через проекции векторов на оси X,Y, после преобразований имеет вид:
 .
(5.13)
.
(5.13)
Вышеприведённые расчеты кинематических и силовых величин целесообразно производить с применением компьютерной техники. При выполнении курсовой работы по ТММ студентам выдается более простой вариант задания, позволяющий использовать лишь инженерный калькулятор.
Расчет перемещений, аналогов скоростей и ускорений ползуна можно вести по приближенным зависимостям (3.13-3. 15).
При силовом расчете учитываются лишь наиболее значимые нагрузки, приложенные на ползуне:
а)
сила сопротивления P
на ползуне, направленная против его
скорости
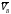 ;
;
б)
сила тяжести ползуна
 ;
;
в)
сила инерции
 .
.
Угловая
скорость кривошипа
 считаетсяпостоянной (
считаетсяпостоянной ( ).
).
В этом случае все полученные зависимости значительно упрощаются. Приведем их для двух наиболее распространенных вариантов расположения схемы механизма.
Вертикальное расположение ползуна.
Ползун
находится ниже центра вращения кривошипа.
Угол
 между осью X
и вектором силы тяжести равен
между осью X
и вектором силы тяжести равен
 .
Схема механизма для данного варианта
вместе с приложенными силами приведена
на рис. 5.7.
.
Схема механизма для данного варианта
вместе с приложенными силами приведена
на рис. 5.7.

Рис.5.7
Преобразуя
вышеприведённые зависимости получим:
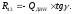 (5.14)
(5.14)
Здесь
 (рис.5.7) (5.15)
(рис.5.7) (5.15)
 —
динамическое
усилие на ползуне от действия внешних
сил и сил инерции.
—
динамическое
усилие на ползуне от действия внешних
сил и сил инерции.
 .
(5.16)
.
(5.16)
Если в рассмотренном положении механизма усилие P направлено против оси X, то подставляем его величину в зависимость (5.16) со знаком “–”.
Так
как внешние силы и инерционные нагрузки,
приложенные к шатуну и кривошипу, не
учитываются :
 .
(5.17)
.
(5.17)
В проекциях на оси X,Y системы координат

 .
(5.18) Полная
величина реакции (по модулю)
.
(5.18) Полная
величина реакции (по модулю)
 .
(5.19 )
.
(5.19 )
Уравновешивающий момент на валу кривошипа
 .
(5.20)
.
(5.20)
Знак
“+” в результатах при расчете по формуле
(5.20) означает, что
 —
движущий момент, знак “–” - момент
сопротивления.
—
движущий момент, знак “–” - момент
сопротивления.
Горизонтальное расположение ползуна.
Ползун
находится слева от центра вращения
кривошипа. Угол
 между осью X
и вектором силы тяжести равен
между осью X
и вектором силы тяжести равен
 .
Схема механизма для данного варианта
вместе с приложенными силами приведена
на рис.5.8.
.
Схема механизма для данного варианта
вместе с приложенными силами приведена
на рис.5.8.

Рис.5.8
Преобразуя зависимости, приведенные в разд. 2, получим
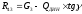 .
(5.21)
.
(5.21)
Здесь
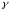 определяется по зависимости (5.15).
определяется по зависимости (5.15).
 –
динамическое
усилие на ползуне от действия внешних
сил и сил инерции
–
динамическое
усилие на ползуне от действия внешних
сил и сил инерции
 .
(5.22)
.
(5.22)
Величину
P
подставляем в зависимости со знаком
“+”, если в данном положении механизма
она направлена по оси X,
и со знаком “–”, если против оси X.
Реакции
 момент
момент
 определяются по зависимостям (5.17),
(5.18), (5.20), (5.20) с использованием зависимости
(5.22).
определяются по зависимостям (5.17),
(5.18), (5.20), (5.20) с использованием зависимости
(5.22).
По
результатам расчетов можно построить
годограф реакции
 (рис. 5.9) и графики
(рис. 5.9) и графики
 и
и
 ,
,
 в зависимости от угла поворота кривошипа
в зависимости от угла поворота кривошипа
 (рис. 5.10; 5.11). Зная в каждом положении
величину М1,
можно найти его среднюю величину МСР
за цикл и определить ориентировочную
величину необходимой мощности на
кривошипе ( в ваттах) N= МСР*
(рис. 5.10; 5.11). Зная в каждом положении
величину М1,
можно найти его среднюю величину МСР
за цикл и определить ориентировочную
величину необходимой мощности на
кривошипе ( в ваттах) N= МСР* СР
СР
В одном из положений механизма можно построить проверочный план сил для ползуна (рис. 5.12). Должно выполняться условие равновесия сил:
 .
(5.23)
.
(5.23)

Рис.5.9
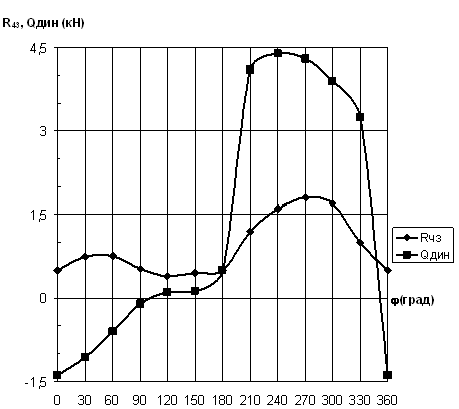
Рис.5.10

Рис.5.11

Рис.5.12
Лекция№6
Уравновешивание инерционных нагрузок.
Механизм является уравновешенным, если, работая на установившемся режиме, он действует на фундамент с некоторыми постоянными по величине и направлению силами и моментами. В действительности звенья движутся с переменными скоростями, а траектории их точек непрямолинейны. Кроме того, неизбежные погрешности изготовления и монтажа. Неоднородность материала и деформации звеньев вызывают смещение центра масс S системы. Указанные обстоятельства вызывают динамические нагрузки в кинематических парах, звеньях, приводят к вибрациям и нарушению плавности движения. Массы звеньев, силы инерции которых вызывают дополнительные нагрузки на опоры, называются неуравновешенными массами. Устранение или уменьшение дополнительных динамических нагрузок на опоры механизма называют уравновешиванием масс. Особенное значение уравновешивание имеет при больших скоростях вращения ,так как величины инерционных нагрузок пропорциональны квадрату угловой скорости ведущего звена механизма.
Статическое уравновешивание рычажных механизмов.
Если
главный вектор сил инерции , который
представляет собой векторную сумму сил
инерции всех подвижных звеньев (например,
рис.5.4) ,
 ,то
такой механизм называется статически
уравновешенным.
,то
такой механизм называется статически
уравновешенным.
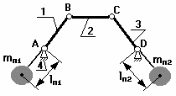
Если
главный момент сил инерции , который
представляет собой векторную сумму
инерционных моментов всех подвижных
звеньев (например, рис.5.4)
,
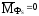 ,,то
такой механизм называется моментно
уравновешенным.
,,то
такой механизм называется моментно
уравновешенным.

Рис.6.1
Рассмотрим случай (рис.6.1), когда механизм необходимо уравновесить статически,
т.е.
 .
Этого можно добиться только тогда, когда
ускорение центра масс
.
Этого можно добиться только тогда, когда
ускорение центра масс .
Для этого нужно, чтобы S à
A.
.
Для этого нужно, чтобы S à
A.
Когда центр масс совмещен с А, то он становиться неподвижным. Этого добиваются с помощью двух противовесов, один из которых устанавливается на продолжении шатуна, а другой на продолжении кривошипа.
Для того чтобы рассчитать массы противовесов, применяют метод замещающих масс, суть которого заключается в том, что масса каждого звена условно разноситься по двум точкам. При этом должны выполняться следующие условия (например для звена АВ):
Разнесем
массу этого звена по точкам А и В так,
чтобы положение центра масс не изменилось.
m = mA + mB
lAB = lAS + lBS
mA lAS = mB lBS
Сосредоточим массу 3-го звена в точке С.
Массу
2-го звена разнесем по шарнирам В и С.
Если на продолжении звена 2 поставить
противовес массой mпр2
и на расстоянии от т.В равное lпр2,
то центр масс звеньев 2 и 3 переместиться
в т.В. При этом

mпр2.lпр2 = (m2C + m3C).lBC
Задаются массой противовеса и определяют lпр2, либо задаются lпр2 и определяют массу противовеса из условия:
mпр1.lпр1 = (m1B + mпр2+ m2В+ m2C+ m3C).lAB
После этого центр масс переместиться в точку А. Однако невсегда конструктивно возможно установить противовес на продолжении шатуна. В этом случае ограничиваются установкой противовеса на звене 1. Центр масс системы смещают на линию АС, который перемещается с линейным ускорением вдоль ползуна. В этом случае механизм – частично статически уравновешен.

Рис.6.2
Его нежелательно устанавливать на высоком фундаменте, т.к. главный вектор сил инерции создает опрокидывающий момент, что недопустимо.
В четырехшарнирном механизме центр масс системы разноситься по точкам А и D, а противовесы устанавливаются на продолжении звеньев 1 и 3.
Следует отметить, что для рычажных механизмов ограничиваются лишь полным или частичным уравновешиванием главного вектора сил инерции. Уравновешивание главного инерционного момента не производится.
Уравновешивание вращающихся звеньев.
Ротор – тело любой геометрической формы, имеющее свое основное движение – движение вращения (коленвал, колесо турбины и т.д.).
Пусть в силу каких-либо причин центр масс ротора смещен от оси вращения О на постоянную величину ест.
Если w=0 , на опоры действует только сила тяжести G=mg. (рис.6.3)


Рис.6.3 Рис.6.4
При вращении ротора (рис.6.4) возникает центробежная сила инерции ФS.
Если
заменить воздействие опоры реакцией и
записать условие статического равновесия
(по принципу Даламбера):

Из рассмотрения данного треугольника следует, что при вращении ротора на его опоре возникает знакопеременная нагрузка Q12, которая достигает максимума, когда ФS и G направлены вниз, и минимума, когда эти вектора направлены по вертикали в разные стороны.
Состояние ротора , характеризующегося таким распределением масс, при котором на его опорах возникает знакопеременная нагрузка, называется неуравновешенностью ротора.
Причины вызывающие неуравновешанность ротора:
-
неточность изготовления ротора;
-
неточность сборки;
-
различные включения при отливке частей ротора;
-
перепады температур.
Мерой
неуравновешенностью ротора является
дисбаланс ( )
– вектор, направленный по ФS
.
)
– вектор, направленный по ФS
.
 ,[г.мм]
,[г.мм]
Для того чтобы определить величину и направление D, в рассмотрение вводят плоскость дисбаланса, в которой этот вектор расположен, и угол дисбаланса.
Процесс определения величины и направления D, и его последующего устранения, называется уравновешиванием ротора или балансировкой.
Существуют 3 вида неуравновешенности:
-
статическая;
-
моментная;
-
динамическая (общий случай).
Статическая неуравновешенность ротора и способы ее устранения
.
Статическая неуравновешенность характеризуется тем, что главная центральная ось инерции ротора расположена параллельно оси его вращения, а центр масс ротора смещен от оси вращения на величину е статическое.
Статическая неуравновешенность проявляется в статике: если ротор установить на призмы, то он, стремясь занять положение устойчивого равновесия, будет поворачиваться.

Рис.6.5
Для устранения статической неуравновешенности по линии действия Dcт устанавливают корректирующую массу mk на расстоянии еk от оси вращения, и эта корректирующая масса создает дисбаланс:

Для статического уравновешивания необходимо, чтобы
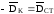
при этом можно задаться величиной m и определить еk , или задаться еk и найти m.
В результате уравновешивания главная центральная ось инерции должна совпасть с осью вращения.
Однако
бывают случаи, когда в силу конструктивных
особенностей ротора нельзя установить
одну корректирующую массу. Тогда
устанавливают две корректирующих масс
в разных плоскостях.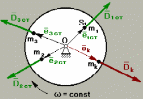
Бывает другой случай статической неуравновешанности, когда ротор по своему объему имеет какие-либо включения сторонних предметов или частиц.
