31) Выносной элемент

При выполнении чертежей в некоторых случаях появляется необходимость в построении дополнительного отдельного изображения какой-либо части предмета, требующей пояснений в отношении формы, размеров или других данных. Такое изображение называется выносным элементом. Его выполняют обычно увеличенным. Выносной элемент может быть выложен как вид или как разрез.

При построении выносного элемента соответствующее место основного изображения отмечают замкнутой сплошной тонкой линией, обычно овалом или окружностью, и обозначают заглавной буквой русского алфавита на полке линии-выноски. У выносного элемента делается запись по типу А (5 : 1). На рис. 191 приведен пример выполнения выносного элемента. Его располагают возможно ближе к соответствующему месту на изображении предмета.

Рифление

Риски на поверхности (как правило, цилиндрической), наносимые для улучшения сцепляемости поверхности детали в эргономических целях … .

32) Способы преобразования геометрических чертежей: Способ замены плоскостей проекции, способ вращения, плоскопараллельного перемещения.

Сущность этого способа заключается в том, что пространственные положения заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекции вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задаче положении..

Последовательность графических построений при решении задач по определению углов наклона плоскости к плоскостям проекция способом замены плоскостей проекций

Для определения угла наклона плоскости треугольника ABC к плоскости проекций П1 или П2 необходимо преобразовать исходный чертеж так, чтобы заданная плоскость заняла проецирующее положение в новой системе плоскостей проекций. Если нужно определить угол наклона атреугольника ABC к плоскости П1, то плоскость проекций П1 оставляют неизменной, а заменяют плоскость П2 на плоскость П3, одновременно перпендикулярную к плоскости П1 и плоскости треугольника ABC. Если необходимо определить угол наклона треугольника ABC к плоскости П2, то оставляют неизменной плоскость проекций П2, а заменяют плоскость П1 на плоскость П3, одновременно перпендикулярную к плоскости П2 и плоскости треугольника ABC. Построение. Заменой фронтальной плоскости проекций П2 преобразуем чертеж так, чтобы основание пирамиды ABC заняло проецирующее положе-

ние по отношению к новой плоскости проекций П3. Для этого:

1. Через вершину C проводят горизонталь треугольника ABC.

2 2. Заменяют плоскость П2 на новую плоскость проекций П3, перпендику-

лярную как плоскости П1, так и плоскости треугольника ABC. На чертеже

новую ось проекций Х1 проводят перпендикулярно к горизонтальной

проеции горизонтали h’.

3. Строят проекции вершин треугольника ABC на плоскость П3. Для это-

го через точки A ’, B ’, С ’ проводят линии связи, перпендикулярные к но- вой оси Х1. Откладывают на них отрезки, равные расстоянию от заменяе-

мых проекций точек A ’’, B ’’, C ’’ до предыдущей оси Х. Проекция тре-

угольника AВС вырождается на плоскости П3 в отрезок прямой линии

(A ’’’ B ’’’ C ’’’), так как треугольник ABC ⊥П3.

4. Искомый угол наклона αo плоскости треугольника ABC к плоскости П1

определяется углом наклона вырожденной проекции (A ’’’ B ’’’ C ’’’) к осиХ1.

Последовательность графических построений при решении задач по определению истинных размеров плоской фигуры

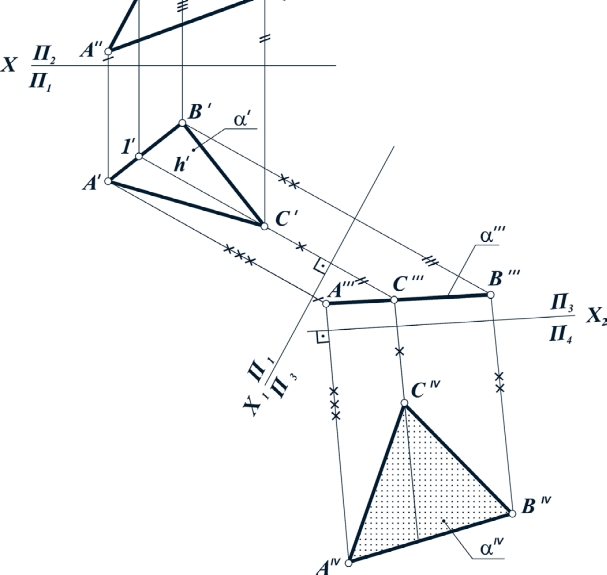
В начале заменяем плоскость П2 на П4 При этом П4 проведем перпендикулярно плоскости АВС (Перпендикулярно горизонтали лежащей в этой плоскости) в результате этой замены плоскость АВС спроецировалась в прямую линию А4В4С4. Затем заменяем плоскость П1 на П5 при этом П5 проведем параллельно получившейся прямой. В результате этой замены получаем плоскость А5В5С5 которая равна натуральной величине плоскости АВС

33)Способ вращения. Сущность этого способа заключается в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических элементов относительно плоскостей проекций путем их вращения вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей. В качестве осей вращения удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точки будут вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

1) Объект вращения. Под объектом вращения следует понимать точку на геометрическом теле. Поэтому в каждой задаче важно определить точки, которые будут вращаться и конечное положение которых надо определить, чтобы получить решение;

2) Ось вращения (выбирается произвольно, если не задана);

3) Плоскость вращения объекта. Она проводится перпендикулярно оси вращения;

4) Центр вращения объекта. Это точка пересечения оси с плоскостью вращения;

 Натуральную величину плоской фигуры удобнее находить с помощью вращения вокруг прямой уровня. Путем такого вращения плоскость, которой принадлежит рассматриваемая фигура, поворачивают в положение, параллельное плоскости проекций. При таком положении плоскости любая принадлежащая ей фигура будет проецироваться в натуральную величину.Вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости П₁. Вращение плоскости вокруг фронтали позволяет перевести ее в положение, параллельное плоскости П₂.На рис.6.3 рассмотрено нахождение натуральной величины треугольника АВС при помощи вращения его вокруг горизонтали.    Каждая точка плоскости треугольника АВС при вращении перемещается по окружности, перпендикулярной оси вращения. Так, точка В перемещается по окружности, плоскость которой перпендикулярна горизонтали. Центр окружности О находится на оси вращения, а величина радиуса равна расстоянию от точки до оси вращения. Так как точка В вращается вокруг горизонтали, то окружность проецируется на П₁ в отрезок прямой, перпендикулярный горизонтали, а на П₂ - в эллипс, который можно не строить.