17)Взаимно перпендикулярные плоскости

а) проекциями трех точек, не лежащих на одной прямой

б) проекциями прямой и точки, взятой вне прямой

в) проекциями двух пресекающихся прямых

г) проекциями двух параллельных прямых

д) проекциями любой плоской фигуры – треугольником, многоугольником, кругом и т.д.

е) более наглядно плоскость может быть изображена при помощи следов – линий пересечения ее с плоскостями проекций

Положение плоскости в пространсвет определяется положением задающих ее фигур.

Прямая линия перпендикулярна плоскости если она перпендикулярна любым двум пересекающимся прямым этой плоскости.

Две плоскости взаимно перпендикулярны если одна из плоскостей имеет прямую линию перпендикулярную другой плоскости.

Прямая линия так же перпендикулярна плоскости если ее проекции перпендикулярны одноименым проекциям направлений горизонтали и фронтали.

Две плоскости могут быть паралельны, пересекаться, быть взаимно перпендикулярными.

Построение взаимно параллельных плоскостей.

Известно, что две плоскости параллельны, если двум пересекающимся прямым, лежащим в одной плоскости, соответствуют две параллельные пересекающиеся прямые другой плоскости. Если же плоскости заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноименных следов (так способ задания плоскости следами есть частный случай задания ее пересекающимися прямыми). Построение параллельных плоскостей на чертеже удобно выполнять с помощью главных линий плоскости - горизонталей и фронталей.

Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям. Или одной точкой , принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух плоскостей.

Общий прием построения линии пересечения двух плоскостей заключается в следующем: вводят вспомогательную плоскость, строят линии пересечения вспомогательной плоскости с двумя заданными и в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

Однако о параллельности профильно проецирующих плоскостей в пространстве можно судить, лишь построив их профильные следы.

Две плоскости пересекаются по прямой линии, общей для обеих плоскостей. Положение прямой линии определяется положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух плоскостей достаточно определить две точки, общие для обеих заданных плоскостей. Если плоскости заданы следами (рис. 4.1), то наиболее рационально отметить точки, являющиеся точками пересечения их одноименных следов (точки M и N прямой MN - линии пересечения плоскостей P и Q).

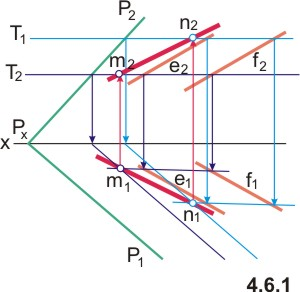
Если же пересекающиеся плоскости (или одна из них) заданы не следами, то для построения линии пересечения их применяется метод вспомогательных секущих плоскостей. Сущность этого метода состоит в том, что обе заданные плоскости пересекаются третьей (обычно плоскостью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной плоскости с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных плоскостей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости. (Задача: На рис. 4.6.1 показано построение линий пересечения двух плоскостей, одна из которых задана следами, а вторая - параллельными прямыми. В качестве вспомогательных секущих плоскостей использованы горизонтальные плоскости Т₁ и Т₂.)

Перпендикулярность плоскостей.