5. Практикум

1. Прямая проходит через точку в направлении вектор нормали:

а) записать общее уравнение плоскости в пространстве;

б) найти отрезки отсекаемые плоскостью на соответствующих осях;

в) найти расстояние от прямой до начала координат.

1. ,; 2.,;

3. ,; 4.,;

5. ,; 6.,;

7. ,; 8.,;

9. ,; 10.,.

2. Записать уравнение плоскости, проходящей через прямую , ортогонально плоскости.

1. ,;

2. ,;

3. ,;

4. ,;

5. ,;

6. ,;

7. ,;

8. ,;

9. ,;

10. ,.

3. Найти проекцию точки на плоскость.

1. ,;

2. ,;

3. ,;

4. ,;

5. ,;

6. ,;

7. ,;

8. ,;

9. ,;

10. ,.

3. Проверить, пересекаются ли прямые и. Если нет, найти расстояние между ними.

1. ,;

2. ,;

3. ,;

4. ,;

5. ,;

6. ,;

7. ,;

8. ,;

9. ,;

10. ,.

3. Вычислить угол между прямой и плоскостью. Составить уравнение проекцим прямой на заданную плоскость.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

3. Записать в общем виде уравнение плоскости проходящей через заданные точки . Вычислить вектор нормали и отрезки, отсекаемые плоскостью на осях координат.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

3. Записать уравнение плоскости проходящей через точку в направлении векторови. Вычислить вектор нормали к данной плоскости

1. , ,;

2. , ,;

3. , ,;

4. , ,;

5. , ,;

6. , ,;

7. , ,;

8. , ,;

9. , ,;

10. , ,.

6. Решение типового варианта

1. Плоскость проходит через точку в направлении вектор нормали:

а) записать общее уравнение плоскости в пространстве;

б) найти отрезки отсекаемые плоскостью на соответствующих осях;

в) найти расстояние от плоскости до начала координат.

Решение:

а) Искомая плоскость проходит через точку и имеет нормальный вектор(рис.1.1), воспользуемся формулой (1.1):

;

раскрывая скобки и приводя подобные, получим общее уравнение плоскости;

б) В полученном общем уравнении перенесем свободный член вправои разделим все на:. Перепишем уравнение в виде (1.3):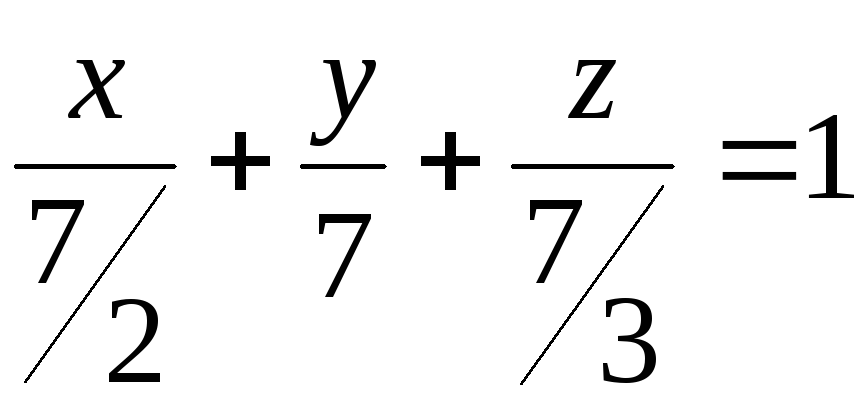. Выражения, стоящие в знаменателях и есть искомые отрезки отсекаемые плоскостью на соответствующих координатных осях.

Для определения отрезков можно воспользоваться и формулами - отрезок отсекаемый плоскостью на оси;- отрезок отсекаемый плоскостью на оси;- отрезок отсекаемый плоскостью на оси.

в) Воспользуемся формулой (2.4), где ,,,- коэффициенты взятые из уравнения плоскости (см. пункт а)),- координаты точки начала координат, получим:

.

2. Записать уравнение плоскости, проходящей через прямую , ортогонально плоскости.

Решении 1:

Искомая плоскость проходит через прямуюи ортогональна заданной плоскости(рис. 6.1). Прямаязадана в каноническом виде (3.3), т.е. некоторой точкойи направляющим векторомкоторый в свою очередь коллинеарен искомой плоскостии будет является для нее первым направляющим вектором.

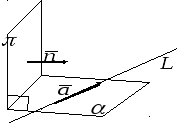
Рис.6.1

Уравнение плоскости задано в общем виде (1.2), т.е. вектором нормали, который также коллинеарен искомой плоскости и является для нее вторым направляющим вектором.

Используя формулу (1.5) запишем уравнение искомой плоскости проходящей через точку в направлении векторови:

.

Раскрывая определитель по первой строке и приводя подобные, получим искомое уравнение

;

Или окончательно: .

Решение 2: В качестве вектора нормали искомой плоскости можно взять вектор, полученный как векторное произведение векторови:

или в координатной форме .

Воспользуемся формулой (1.1). Координаты точки можно взять из уравнения прямой.

, преобразуем его и получим:

.

3. Найти проекцию точки на плоскость.

Решение:

Опустим перпендикуляр из точки на плоскость. Обозначим его, а точку пересечения прямойи плоскостиобозначим точкой. Точкаи будет искомой проекцией (рис.6.2) .

Рис.6.2

Запишем уравнение прямой используя формулу (3.3),- координаты точки, в качестве направляющего вектора прямой возьмём коллинеарный ей вектор нормалиплоскости, тогда. Чтобы найти координаты точки, пересечения прямой и плоскости, решим систему:

,

Для ее решения необходимо уравнение прямой записать в параметрическом виде, т.е. приравняем пропорции параметру:, и выразим переменные:

,

Полученные выражения подставим в первое уравнение системы

;

выразим параметр :,,.

Найдём , подставляя найденное значениев систему:

;

;

.

Это и есть координаты искомой точки .

4. Проверить, пересекаются ли прямые и. Если нет, найти расстояние между ними.

Решение:

Чтобы проверить пересекаются ли прямые необходимо проверить их на принадлежность одной плоскости (компланарность). Условие компланарности – это равенство нулю смешанного произведения трех векторов. Два из них –направляющие вектора прямых: ,. Еще один вектор мы построим на координатах точекитакже взятых из канонических уравнений прямыхи:. Тогда условие компланарности прямых запишется в виде:

;

следовательно, прямые не лежат в одной плоскости не пересекаются и не являются параллельными (в это случае определитель был бы также равен нулю), т.е. они скрещивающиеся и расстояние между ними можно найти как высоту параллелепипеда (рис. 6.3)

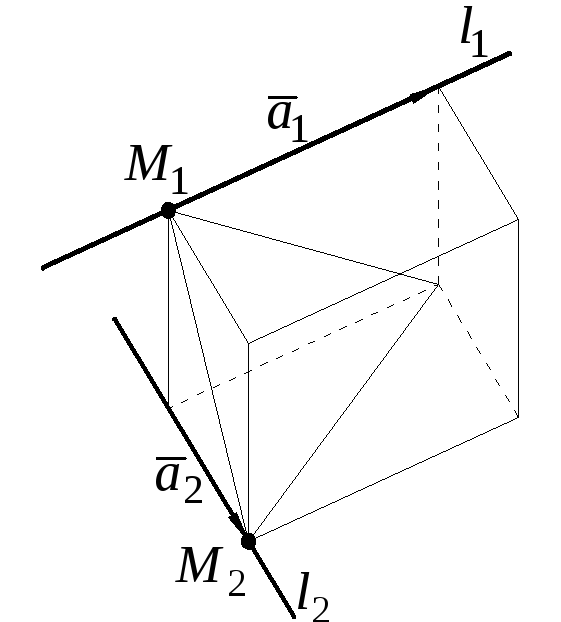
Рис. 6.3

Объем параллелепипеда определим как модуль смешанного произведения векторов , получим. Площадь основания вычислим как модуль векторного произведения векторови.

. Или , тогда. Окончательно получим:.

5. Вычислить угол между прямой и плоскостью. Составить уравнение проекции прямой на заданную плоскость.

Решение:

Запишем уравнение прямой в каноническом виде (3.3). Для этого нам необходимо определить координаты точки принадлежащей прямой и направляющий вектор этой прямой. Для определения координат точки решим систему уравнений.

Т.к. все три переменные пробегают всю числовую прямую, возьмём напримери подставим в систему. Определим теперь переменныеи: умножим второе уравнение наи сложим с первым:

откуда . Умножим второе уравнение наи сложим с первым:

откуда .

Координаты точки принадлежащей прямой.

Найдём координаты направляющего вектора прямой. Вектора нормали к плоскостям будут ортогональны этому вектору и следовательно, можно найти его воспользовавшись свойством векторного произведения:, гдеипо условию. Тогда

;

Координаты вектора . Запишем уравнение прямойв каноническом виде по формуле (3.3):

;

;

Окончательно: .

Найдём угол между прямой и плоскостьюпо формуле (4.3). Где,- вектор нормали плоскости.

.

Определим проекцию прямой. Плоскостьпроведенная ортогонально плоскостии содержащая в себе прямуюна пересечении с плоскостьюобразуют искомую проекцию(рис. 6.4).

Рис.6.4

Составим уравнение плоскости используя формулу (1.5). Направляющими векторами здесь будут векторы- направляющий прямойи- нормаль к плоскости. Координаты точки определим из канонического уравнения прямой. Получим:

;

Раскроем определитель по элементам первой строки

;

;

окончательно получим - уравнение плоскости.

Тогда наша проекция может быть записана в виде пересечения плоскостейи:.

6. Записать в общем виде уравнение плоскости проходящей через заданные точки . Вычислить вектор нормали и отрезки, отсекаемые плоскостью на осях координат.

Решение:

Для нахождения уравнения плоскости воспользуемся формулой (1.4), где - координаты точки;- координаты точки;- координаты точкисоответственно:

или .

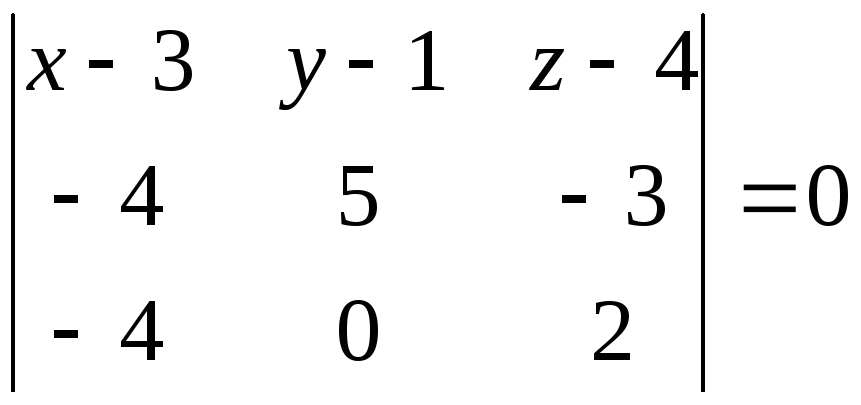Вычислим определитель разложением по первой строке:

;

Приводим подобные, полученный результат делим на :

;

- уравнение искомой плоскости.

Координаты вектора нормали это коэффициенты уравнения при неизвестных , то есть. Отрезки, отсекаемые плоскостью на осях координат, находим приводя уравнение к виду (1.3):

, ,,

.

отрезок на оси ,отрезок на оси,

отрезок на оси .

6. Записать уравнение плоскости проходящей через точку в направлении векторови. Вычислить вектор нормали к данной плоскости.

Решение:

Используя формулу (1.5) запишем уравнение плоскости:

Раскрываем определитель по первой строке и приводим подобные:

;

.

Получили общее уравнение плоскости. Откуда согласно формуле (1.2) определяем координаты вектора нормали:

.