федеральное агенство по образованию

Дальневосточный государственный технический университет

(ДВПИ им. В.В. Куйбышева)

Прямая и плоскость в пространстве Практикум

Методические указания по проведению практических занятий для студентов технических специальностей

Владивосток 2010

Одобрено методическим советом университета

УДК 519

Прямая и плоскость в пространстве.: метод. указания / Сост. Н.Е. Дегтярева, Е.В. Агеева – Владивосток: Изд-во ДВГТУ, 2011. – 24с.

В краткой форме излагается основной теоретический материал, входящий в раздел аналитической геометрии: понятие прямой и плоскости, определение расположения прямой и плоскости в пространстве, углы между прямыми и плоскостями, определение расстояний. Содержит 10 вариантов заданий для самостоятельной работы студентов, дополнительные задания. В решении типового варианта рассмотрены различные методы решения задач.

Методические указания предназначены для студентов технических специальностей.

Методические указания печатаются с оригинал-макета, подготовленного авторами

©Н.Е.Дегтярева

©Изд.-во ДВГТУ, 2011

1. Уравнения плоскости в пространстве.

Произвольный вектор ортогональный к плоскости(рис.1.1) называется еёнормальным вектором или нормалью к плоскости.

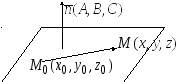
Рис.1.1

Пусть , изаданная точка плоскости, тогда из условия ортогональности векторов(здесь и далеепроизвольная точка плоскости), получим:

(1.1)

- уравнение плоскости проходящей через данную точку в направлении данного вектора нормали.

Раскрывая скобки, и вводя новую константу , получим:

(1.2)

– общее уравнение плоскости.

Преобразовав формулу (1.2) получим уравнение плоскости в отрезках: (1.3)

где 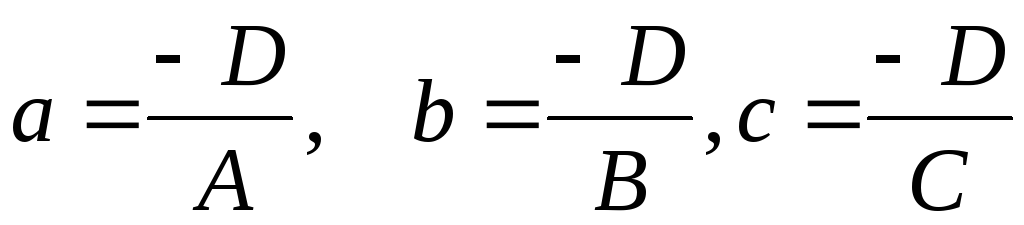- отрезки, отсекаемые плоскостью на координатных осях,исоответственно (рис.1.2).

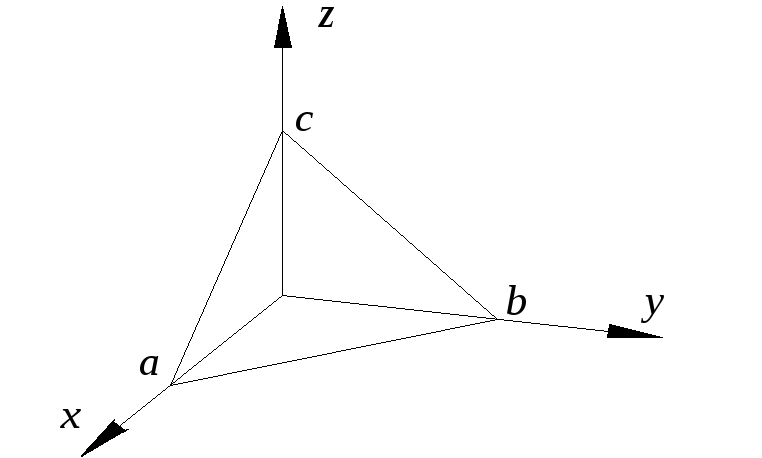
Рис.1.2

Три точки ,, лежат в одной плоскости (рис. 1.3) тогда и только тогда, когда векторы ,,компланарны:.

Рис.1.3

Или в координатной форме:

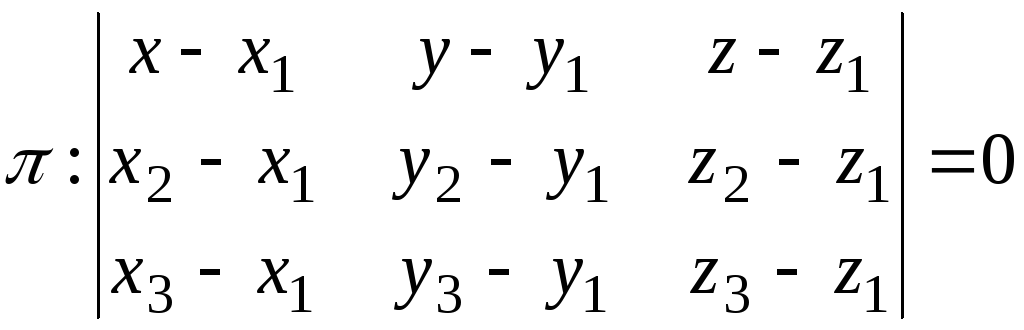(1.4)

уравнение плоскости проходящей через три точки.

Два неколлинеарных между собой вектора принадлежащих одной плоскости или параллельных ей, называются направляющими к этой плоскости.

Для того, чтобы записать уравнение плоскости, проходящей через заданную точку и два направляющих вектора плоскости , воспользуемся условием компланарности векторов(рис.1.4).

Рис.1.4

или в координатной форме:

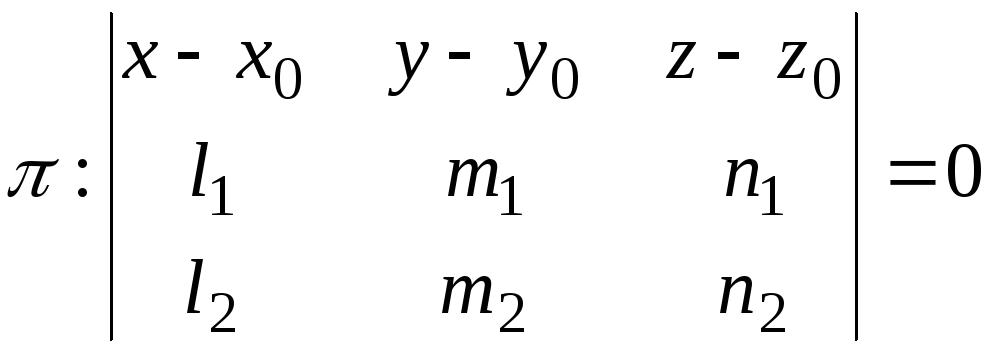(1.5)

2. Угол между двумя плоскостями. Условия параллельности и ортогональности плоскостей. Расстояние от точки до плоскости

Пусть даны две плоскости: ,

. Угол между плоскостями можно определить как угол между их направляющими векторами и(рис. 2.1).

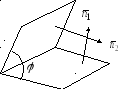
Рис. 2.1

(2.1)

Если , то и соответствующие координаты векторов пропорциональны:

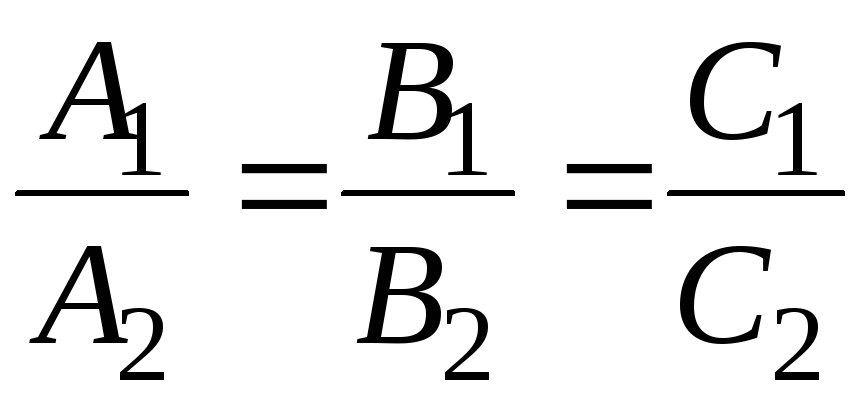(2.2)

Если , тои скалярное произведение этих векторов равно нулю

_(2.3)

_{При решении задач используется формула определения расстояния от точки}

до плоскости заданной общим уравнением

. Данное расстояние вычисляется по формуле:

_(2.4)

3. Уравнения прямой в пространстве

Прямую можно задавать либо двумя уравнениями плоскостей:

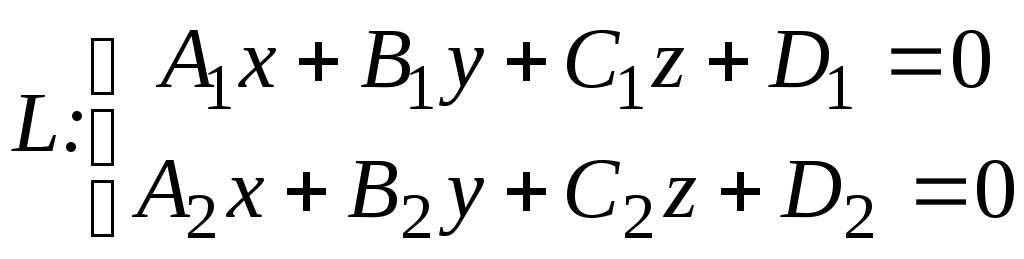(3.1)

Либо пучком плоскостей, проходящих через эту прямую:

(3.2)

Каждый ненулевой вектор будем называтьнаправляющим вектором этой прямой. Уравнение прямой, проходящей через заданную точку и имеющей заданный направляющий векторполучим из условия коллинеарности векторов(рис.3.1):

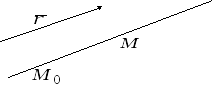
Рис.3.1

Векторы коллинеарны, следовательно их соответствующие координаты пропорциональны:

(3.3)

Уравнение (3.3) принято называть каноническим уравнением прямой.

Уравнение прямой, проходящей через две заданные точки и можно записать используя тоже свойство коллинерности векторов и(рис. 3.2)

Рис.3.2

Получим уравнение прямой проходящей через две точки:

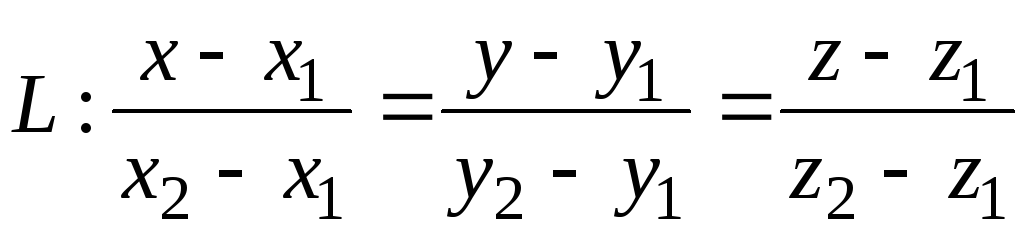(3.4)

Приравняем уравнение (3.3) произвольному параметру :

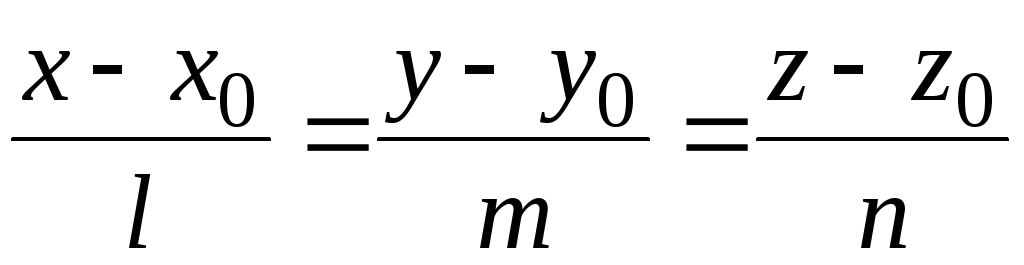
_{Получим систему равенств}

, ,;

_{определяющих параметрическое уравнение прямой:}

_(3.5)

4. Угол между прямой и плоскостью. Условие параллельности и ортогональности двух прямых, прямой и плоскости.

Рассмотрим пару прямых и. Расположение прямых в пространстве можно рассмотреть по расположению их направляющих векторови.

Если прямые параллельны, то координаты их направляющих векторов пропорциональны:

(4.1)

Если прямые ортогональны, то скалярное произведение их направляющих векторов равно нулю:

_(4.2)

Рассмотрим плоскость , и прямуюимеющую направляющий вектор. Пустьφ – угол между прямой и плоскостью(рис. 4.1).

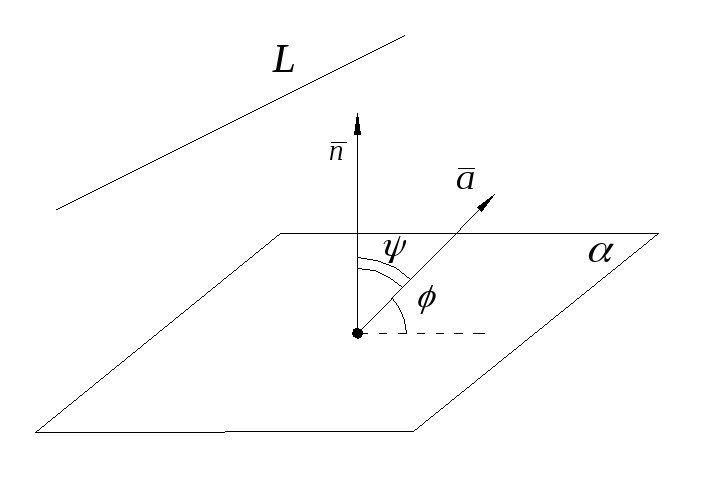
Рис.4.1

Так как ,,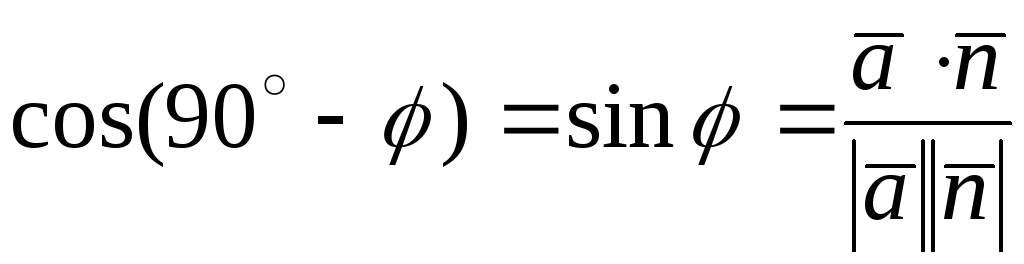 тогда

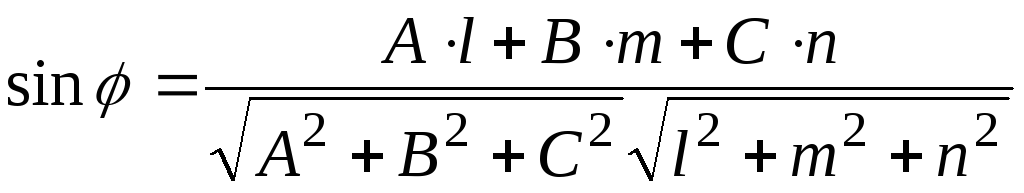(4.3)

Условие коллинеарности и ортогональности прямой и плоскости выводится из взаимного расположения их направляющих векторов:

1) если , тои следовательно,

(4.4)

2) если , тои их координаты пропорциональны

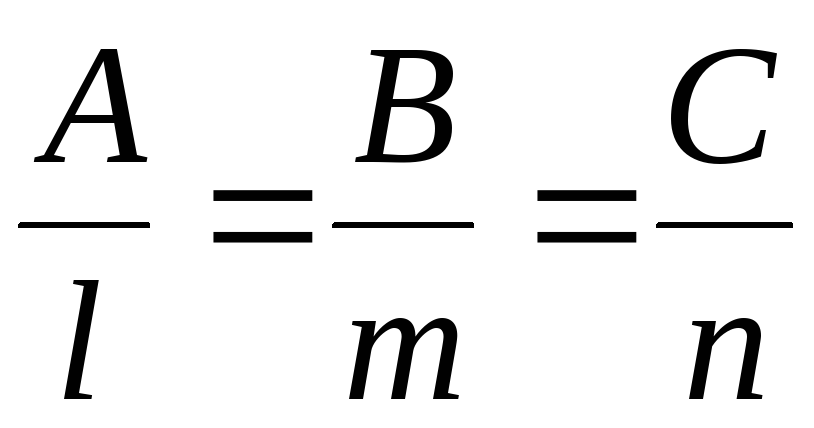(4.5)