2.2.2. Теоремы

Теперь сформулируем теоремы о свойствах основной задачи ЛП.

Теорема 1.

Множество планов основной задачи ЛП является выпуклым (если оно непусто).

Теорема 2.

Если основная задача ЛП имеет оптимальный план, то максимальное значение целевая функция принимает в одной из вершин многогранника решений.

Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.

2.3.Переход от одной формы задачи лп к другой

Как уже было сказано выше, существуют стандартная форма задачи линейного программирования и каноническая форма. В любом случае ищется экстремум целевой функции, т.е. либо максимум, либо минимум. Таким образом, можно выделить задачи на максимум и задачи на минимум. Существуют правила перехода от одной формы задачи ЛП к другой, т.е. переход от задачи на поиск максимума целевой функции к задаче поиска минимума целевой функции целевой функции (FmaxFmin), а также переход от стандартной задачи ЛП к канонической и наоборот (стандартнаяканоническая). Рассмотрим эти правила.

2.3.1. Сведение задачи минимизации к задаче максимизации:

F=c₁x₁+c₂x₂+ …c_nx_nminсводится к

F = -F = - c₁x₁ - c₂x₂ - … c_nx_n  max;

2.3.2. Переход от стандартной задачи к канонической.

Ограничение – неравенство () исходной задачи можно преобразовать в ограничение – равенство добавлением к его левой части дополнительной неотрицательной переменной, т.е.

_i1х₁+_i2х₂+_i3x₃+ …_{in } х_n ()b_iпреобразуется в

_i1х₁ + _i2 х₂ + _i3x₃ + _in х_n + x_n+1 = b_i

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений – неравенств в ограничение – равенства равно числу преобразуемых неравенств.

2.3.3. Переход от канонической задачи к стандартной:

_i1х₁+_i2х₂+_in х_n=b_i

можно записать в виде неравенств

_i1х₁ + _i2 х₂ + … _in х_n  b_i

 _i1х₁  _i2 х₂  … _in х_n   b_i

3. Методы решения задач нелинейного программирования.

Геометрическая интерпретация

3.1. Геометрический способ

3.1.1. Пример геометрической интерпретации задачи ЛП

3.1.2. Этапы решения задачи

Существуют два основных метода решения задачи линейного программирования: решение на основе геометрической интерпретации (геометрический способ) и так называемый симплекс-метод.

3.1. Геометрический способ.

Геометрический способ может быть применен только для двумерных задач, т.е. при n= 2. В этом случае область допустимых значений –выпуклый многоугольник на плоскости (х₁ , х₂ ), являющийся результатом пересечения полуплоскостей, каждая из которых – решение соответствующего неравенства системы ограничений.

Целевая функция позволяет провести семейство параллельных прямых - так называемых линий уровня, отвечающих определенному значению линейной формы (т.е. целевой функции). При этом, смещение прямой по направлению нормального вектора,координаты которого равны коэффициентам при соответствующих переменных в целевой функции приводит к увеличению значения целевой функции; в противоположном направлении – к уменьшению.

Таким образом, решением задачи будет та угловая точка ОДР, которая является крайней в направлении линии уровня.

Непустое множество задачи ЛП образует выпуклый многогранник. Каждая вершина многогранника представляет собой опорный план. В одной из вершин многоугольника (т.е. для одного из опорных планов значения целевой функции является максимальным (при условии, что функция ограничивает сверху на множестве планов.

Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин. Другими словами, оптимальный план реализуется на границе ОДР или в одном из опорных планов.

Нахождение минимального значения F отличается от нахождения максимального ее значения при тех же ограничениях лишь тем, что ЛУ передвигается не в направлении С, а в противоположном.

Отметим свойства целевой функции и ограничений

1. Целевую функцию можно умножать на любую положительную const.

2. К целевой функции можно добавлять любую const.

3. С ограничениями можно как с системой равенств или неравенств проводить эквивалентные алгебраические преобразования.

Пример: Найти решение задачи ЛП при следующих данных:

F = 2X₁+ 3X₂ ® max при

4X₁+ 3X₂  12 (1)

X₁ - X₂  1 (2)

- X₁ + 6X₂  12 (3)

X₁, X₂  0 (4)

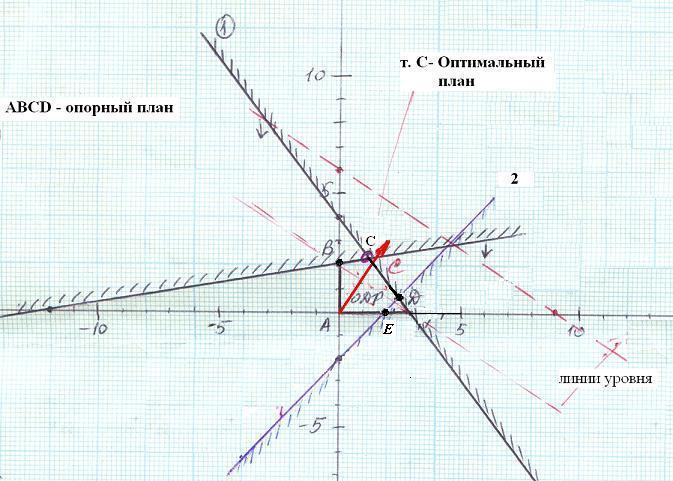
Область допустимых решений задачи (ОДР), или множество планов задачи представляет собой многоугольник, ограниченный прямыми – геометрическим выражением уравнений, преобразованных из неравенств (1)-(3). Поочередно приравнивая в уравнениях (1)-(3) Х₁ и Х₂ к нулю, а также используя условие (4), строим прямые, определяем полуплоскости, соответствующие каждому ограничению задачи и получаем многоугольник ABCD (см. рис.1). Каждая вершина многоугольника представляет собой опорный план.

Примечание: чтобы правильно определить допустимую полуплоскость, удобно ориентироваться по знаку при переменной X₂. Если это минус, а в неравенстве знак  , то допустимые решения будут лежать ниже прямой, если знак  , полуплоскость строится вверх от прямой. Если знак при второй переменной плюс, то, соответственно, плоскости строятся в противоположных направлениях).

В одной из вершин многоугольника (т.е. в одном из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Пункты 1-3 выполнены. Строим направляющий вектор. Начало его совпадает с началом координат, а конец имеет координаты (С₁; С₂), соответствующие коэффициентам в целевой функции. В нашем случае (2; 3).

Рис. 1

Вектор (2; 3) показывает направление роста целевой функции. Для определения вершины многоугольника построим линию уровняF =2X₁+ 3X₂ = h, проходящую через многоугольник решений. Вначале положим h = 6. Нетрудно видеть, что линия уровня перпендикулярна направляющему вектору. Задав новое значение h , больше предыдущего, мы передвигаем линию уровня по направлению вектора . Точка, в которой линия уровня покидает ОДР ( в нашем случае это точкаС) и будет решением задачи, т.е. оптимальным планом. Однако, определив точку на чертеже, необходимо определить точное значение ее координат, т.е. переменных X₁ и X₂. Поскольку точка С находится на пересечении прямых, соответствующих уравнениям (1) и (3), решая совместно эти уравнения, получим значения X₁ = 1,33 и X₂ = 2,22.

Решение записывается в виде X(1,33; 2,22).

Подставив найденные значения переменных в выражение для целевой функции, вычисляем ее максимальное значение: F = 9,33.