
- •1. Структурная схема системы цифровой связи
- •2. Исходные данные для расчета системы цифровой связи
- •3. Расчет системы цифровой связи
- •3.1. Источник сообщения
- •3.2. Аналого-цифровой преобразователь
- •3.3. Кодер
- •3.4. Формирователь модулирующих сигналов
- •3.5. Модулятор
- •3.6. Непрерывный канал
- •3.7. Демодулятор
- •3.8 Декодер
- •График выполнения кр
3.3. Кодер
Используется помехоустойчивый свёрточный код. Выбрать структурную схему свёрточного кодера [1, стр. 251 - 253].
Требуется:
1. Использовать свёрточный код с параметрами:
- степень кодированияk/n= 1/2,
- длина кодового ограниченияK= 3,
- векторы связи g1= 111 иg2= 101.
2. Нарисовать схему кодера,соответствующую заданным параметрам, и определить его импульсную характеристику g(x).











g(x) = 1 +x + x2 + x4+ x5,g = 111011.
3. Изобразить решетчатую диаграмму свёрточного кодера от момента времени t1до момента времениt10.
t1 t2t3 t4 t5t6 t7 t8 t9 t10

Рис. 3.3.2. Решетчатая диаграмма свёрточного кодера
4. На решетчатой
диаграмме свёрточного кодера построить
путь, соответствующий
последовательностиинформационных
символов b(iT)
от АЦП для заданного уровняквантования ,
и определить по нему последовательность
кодовых символовc(iTb)
на выходе кодера.
,
и определить по нему последовательность
кодовых символовc(iTb)
на выходе кодера.
b(iT) = 111110100

c(iTb)= 11 01 10 10 10 01 00 10 11
Рис. 3.3.3. Путь на решетчатой диаграмме кодера для b(iT) = 101110100
Приb(iT) = 111110100c(iTb) = 110110101001001011
5. Определить длительность двоичного символа ТВна выходе кодера (в последовательном формате)

6. Определить техническую скорость передачи VВ
VВ = 1/ТВ=
3.4. Формирователь модулирующих сигналов
Формирователь модулирующих сигналов (ФМС)предназначен для преобразования двоичного цифрового потока от кодера C(t)в модулирующие сигналыI(t) иQ(t), которые необходимо подавать на синфазный и квадратурный входы модулятора для получения заданного сигнального созвездия на его выходе.Ондолжен содержать:
- регистр сдвигадля деления входного потока бит от кодера на группы, передаваемые одним сигналомsКАМ(t) (дибиты приQPSKи квадбиты приQASK);
- преобразователи уровней битовых сигналов(униполярной кодировки в биполярную: приQPSK«0» →h, «1» → –h; приQASK«00» → 3h, «01» →h, «10» → –h, «11» → –3h);
- дополнительно, при QASK, –кодопреобразовательисходного кода квадбит в код Грея для выравнивания минимальных расстояний между сигналами модулятора и соответствующим им квадбитам.
Требуется:
Изобразить сигнальное созвездие для заданного вида модуляции.


а) б)
Рис. 3.4.1. Сигнальные созвездиячетырехуровневой QASK(а) иQPSK(б)
Изобразить график реализации c(t) случайного процессаC(t)
на входе блока ФМС (выходе свёрточного кодера) для первых 16 бинарных интервалов (рис. 3.4.2).

Рис.
3.4.2. Осциллограмма реализации
 с
выхода свёрточного кодера
с
выхода свёрточного кодера
Написать
аналитическое выражение для случайного
процесса
 .
.

где

прямоугольный импульс длительностью
прямоугольный импульс длительностью
 при
при

где

прямоугольный импульс такой же формы,
как
прямоугольный импульс такой же формы,
как ,
но сдвинутыйвправо
относительно импульса
,
но сдвинутыйвправо
относительно импульса
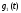 на величину
на величину ,
если
,
если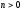 ,
иливлево,
если
,
иливлево,
если
 ;
; - случайная величина 0, +h(значение
бита на
- случайная величина 0, +h(значение
бита на
 - интервале
- интервале ).
).
В соответствии с сигнальным созвездием модулятора QPSK
(или
QASK)изобразить
для входной реализации
 графики реализаций
графики реализаций и
и на выходе блока ФМС случайных процессов
на выходе блока ФМС случайных процессов и
и (рис. 3.4.3).Написать аналитические выражения
для случайных процессов
(рис. 3.4.3).Написать аналитические выражения
для случайных процессов и
и .
.
 ;
;

где
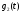
прямоугольный импульс длительностьюTS.
прямоугольный импульс длительностьюTS.



прямоугольный импульс такой же формы,
как импульс
прямоугольный импульс такой же формы,
как импульс
 ,
но сдвинутый вправо относительно
импульса
,
но сдвинутый вправо относительно
импульса на величину
на величину ,
если
,
если ,
или влево, если
,
или влево, если ;
; и
и
независимые случайные величины, заданные
на символьном интервале с номером
независимые случайные величины, заданные
на символьном интервале с номером ,
которые согласно сигнальному созвездию
(рис. 3.4.1) принимают:
,
которые согласно сигнальному созвездию
(рис. 3.4.1) принимают:
дляQPSK два дискретных значения –h, +h с вероятностью 0,5 каждое, т. е.
 ;
;
дляQАSK четыре дискретных значения –3h, –h, +h ,+3h с вероятностями

 для QPSK(вариант
00)
для QPSK(вариант
00)
 для QАSK(вариант
01)
для QАSK(вариант
01)
Рис. 3.4.3.
Осциллограммы реализаций i(t)q(t)навыходах и
и ФМС
ФМС
Написать аналитические выражения для корреляционной функции
 и спектральной
плотности мощности
и спектральной
плотности мощности
 входного случайного процесса
входного случайного процесса и построить графики этих функций.
и построить графики этих функций.
Процесс C(t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид [1]
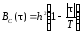 ,
,
а энергетический спектр
 ,
,
где Т = ТВ – длительность тактового интервала.
Графики BC(τ) и GC(f) приведены на рис. 3.4.4.

Рис. 3.4.4. Корреляционная функция BC(τ) (а) и энергетический спектрGC(f) (б)
синхронного телеграфного сигналаC(t)
5. Написать аналитические выражения для корреляционных функций
BI(τ) и BQ(τ), спектральных плотностей мощности GI(f) и GQ(f) случайных процессов I(t) и Q(t). Построить графики этих функций.
Процессы I(t) и Q(t) отличаются от процесса C(t) длительностями тактовых интервалов (TS = 2TBдля QPSK и TS = 4TBдля QАSK), а для QАSK ещё и начальными значениями BI(0) =BQ(0) = D[I(t)] = D[Q(t)] и GI(0) = GQ(0) = D[I(t)]/TS= D[Q(t)]/TS

Графики BI(τ) и GI(f)для QАSK приведены на рис. 3.4.5.

Рис. 3.4.5. Корреляционная функция BI(τ) (а) и энергетическийGI(f) спектр (б)
синхронного телеграфного сигналаI(t)
6. Сравнить графики корреляционных функций и спектральных
плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала.
(Добавить!) 7. Определить длительность символьного интервала TS.
TS = 2TB дляQPSK ,
TS = 4TB дляQPSK,
где TB - бинарный интервал).
