3. Статистика электронов и дырок в полупроводниках

Целью настоящей главы является определение концентраций элек­тронов в зоне проводимости и дырок в валентной зоне полупроводника, возникающих вследствие тепловой генерации в состоянии термодина­мического равновесия. Процессами, приводящими к образованию сво­бодных электронов и дырок, являются

1) переход электронов из ва­лентной зоны в зону проводимо­сти с образованием пары свобод­ных носителей - электрона и дырки;

2) переход электрона с донорного уровня в зону проводимости с образованием свободного электро­на и положительно заряженногоиона донорной примеси N⁺_d;

3) переход электрона из ва­лентной зоны на акцепторный уровень с образованием свободной дырки и отрицательно заряженного иона акцепторной примеси N^-_a .

Электроны, перешедшие в зону проводимости, занимают состоя­ния с наименьшей энергией, т.е. заполняют энергетические уровни вблизи ее дна. Поскольку энергия дырок отсчитывается вниз, они за­нимают состояния с наименьшей энергией вблизи потолка валентной зоны.

Для нахождения равновесных концентраций электронов n₀ и дырок p₀ необходимо знать плотности квантовых состояний в обеих зонах и вероятности заполнения каждого квантового состояния.

Плотность квантовых состояний

При изучении зонной теории было показано, что электроны вблизи дна зоны проводимости ведут себя как свободные частицы, если им приписать эффективную массу m^*_n .

Рассмотрим вначале плотность квантовых состояний для электронов в зоне проводимости в предположении, что эффективная масса электронов m^*_n - скаляр, В этом случае закон дисперсии для электронов

в зоне проводимости (2.8) E()=

Совпадает с зконом дисперсии для электронов в модели Зоммерфельда. Тогда плотность квантовых состояний в зоне проводимости g_n(E) можно легко получить из выражения 1.16, если отсчитывать энетгию от дна зоны:

g_n(E)=( ) (E-E_c)

В общем случа эффективная масса электрона является тензором второго ранга и описывается тремя компонентами: m^*₁ , m^*₂ , m^*₃, а числа эквивалентных минимумов в зоне проводимости равно M_c>1

Расчёт для этого случая даёт выражение g_n(E)=( ) (E-E_c) (3.1), где m_c=называется эффективной массой плотности состояний для электронов. Введение эффективной массы плотности состояний означает замену M_c эквивалентных эллипсоидов равной энергии одной сферической изоэнергетической поверхностью, которая обеспечивает ту же плотность квантовых состояний.

В кремнии в 1 и зоне Бриллюэна имеется шесть минимумов энергии: Мс = 6, а компоненты тензора эффективной массы m^*₁ = m^*₂ = m^*_t =0,19m, m^*₃= m^*_l=0,98m Отсюда m_c = 1,08m

Аналогично рассчитывается плотность квантовых состояний g_р(Е) для дырок в валентной зоне. Полагая началом отсчёта энергии потолок валентной зоны и считая эффективную массу дырок скаляром, получаем

валентной зоны и

g_p(E)=( ) (E-E)

При сложном строении валентной зоны аналогично можно ввести массу плотности состояний m для дырок. Например, в кремнии имеются два вида дырок в валентной зоне с эффективными массами m^*_pл = 0,16m и m^*_pt = 0,49m. Для них можно ввести m_v=( m^*_pл+ m^*_pt)=0,56m

При этом плотность квантовых состояний для дырок в валентной

зоне запишется в виде g_n(E)=( ) (E-E)

5.1. Функция распределения

     В качестве основной функции, применяемой при статистическом методе описания, выступает функция распределения, которая определяет статистические характеристики рассматриваемой системы. Знание её изменения с течением времени позволяет описывать поведение системы со временем. Функция распределения дает возможность рассчитывать все наблюдаемые термодинамические параметры системы.

     Для введения понятия функции распределения сначала рассмотрим какую-либо макроскопическую систему, состояние которой описывается некоторым параметром , принимающим дискретных значений: , , ,..., . Пусть при проведении над системой измерений были получены следующие результаты: значение наблюдалось при измерениях, значение наблюдалось соответственно при измерениях и т.д. При этом, очевидно, что общее число измерений равняется сумме всех измерений , в которых были получены значения : .

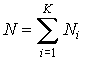     Увеличение числа проведенных экспериментов до бесконечности приводит к стремлению отношения к пределу

     

.

(5.1)

     Величина называется вероятностью измерения значения .

     Вероятность представляет собой величину, которая может принимать значения в интервале . Значение соответствует случаю, когда ни при одном измерении не наблюдается значение и, следовательно, система не может иметь состояние, характеризующееся параметром . Соответственно вероятность возможна только, если при всех измерениях наблюдалось только значение . В этом случае, система находится в детерминированном состоянии с параметром .

     Сумма вероятностей нахождения системы во всех состояниях с параметрами равна единице:

     

.

(5.2)

     Условие (5.2) указывает на достаточно очевидный факт, что если набор возможных дискретных значений , , является полным (то есть включает все возможные значения параметра в соответствии с условиями физической задачи), то при любых измерениях параметра должны наблюдаться значения этого параметра только из указанного набора .

     Рассмотренный нами случай, когда параметр, характеризующий систему, принимает набор дискретных значений не является типичным при описании макроскопических термодинамических систем. Действительно, такие параметры как температура, давление, внутренняя энергия и т.д., обычно принимают непрерывный ряд значений. Аналогично и переменные, характеризующие движение микрочастиц (координата и скорость), изменяются для систем, описываемых классической механикой, непрерывным образом.

     Поэтому рассмотрим статистическое описание, применимое для случая, когда измеренный параметр может иметь любые значения в некотором интервале . Причем, указанный интервал может быть и не ограниченным какими либо конечными значениями и . В частности параметр в принципе может изменяться от до , как, например, координаты молекулы газа для случая неограниченной среды.

     Пусть в результате измерений было установлено, что величина с вероятностью попадает в интервал значений от до . Тогда можно ввести функцию , характеризующую плотность распределения вероятностей:

     

.

(5.3)

     Эта функция в физике обычно называется функцией распределения.

     Функция распределения должна удовлетворять условию: , так как вероятность попадания измеренного значения в интервал от до не может быть отрицательной величиной. Вероятность того, что измеренное значение попадет в интервал равна

     

.

(5.4)

     Соответственно, вероятность попадания измеренного значения в весь интервал возможных значений равна единице:

     

.

(5.5)

     Выражение (5.5) называется условием нормировки функции распределения.

     Функция распределения позволяет определить среднее значение любой функции :

     

.

(5.6)

     В частности по формуле (5.6) может быть найдено среднее значение параметра :

     

.

(5.7)

     Если состояние системы характеризуется двумя параметрами и , то вероятность её нахождения в состоянии со значениями этих параметров в интервалах и соответственно равна

     

,

(5.8)

     где - двумерная функция распределения. Примером такой функции может служить совместное распределение для координат и скоростей молекул газа.

     Соответственно для бесконечно малых интервалов и вероятность можно представить в виде

     

.

(5.9)

     В случае статистической независимости значений параметров и друг от друга двумерная функция распределений равна произведению функций распределения и :

     

.

(5.10)

     Это свойство функций распределения будет нами использовано при рассмотрении распределения Максвелла-Больцмана.

     Задача 5.1. Найти функцию распределения и среднее значение координаты молекулы газа, находящегося в равновесном состоянии в изолированной системе при отсутствии внешних сил. Считать, что молекула может находиться только в интервале координат . Распространить полученный результат на трехмерный случай.

     Решение: Так как газ находится в равновесном состоянии, то вероятность нахождения молекулы в любом интервале значений координаты будет одинаковой и, следовательно, функция распределения . Тогда в соответствии с условием нормировки (5.5) имеем выражение для функции распределения в интервале значений : .

     При или функция распределения .

     Подстановка этого выражения для функции распределения в формулу (5.7) дает среднее значение координаты молекулы газа: .

     Полученные выражения позволяют, с использованием условия независимости переменных , и , аналогично формуле (5.10) записать выражение для трехмерной функции распределения

     

.

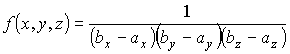     Соответственно средние значения координат , и будут иметь вид:

     

, , .
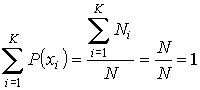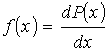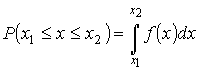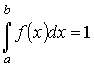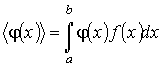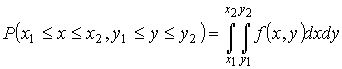