
- •А).Необходимость в зонной теории.
- •Б. Основные понятия зонной теории (определения, постулаты и гипотезы).
- •Можно показать, что скорость групповая равна скорости частицы в классическом понимании. Задача: Показать, что скорость групповой волны равна скорости частицы (использовать:
- •Заметим,
- •В. Основы зонной теории кристаллов
- •Операторы энергии (гамильтониан) и уравнения Шредингера.
- •Стационарные состояния и уравнение Шредингера для стационарных состояний
- •Г. Движение электронов в твердых телах (зонная теория)
- •Связь проводимости со сферой Ферми
В. Основы зонной теории кристаллов
Допущения:
справедлив принцип Паули;
справедлив принцип неразличимости тождественных частиц;
электроны взаимодействуют с трехмерным периодическим полем кристалла;
химическая связь и физические свойства определяются только внешними электронами;
внутренние электроны экранируют внешние электроны от полей ядер, существенно уменьшая эти поля, так что на внешние электроны действует потенциал, который намного меньше потенциала ядра.
Операторы энергии (гамильтониан) и уравнения Шредингера.
![]() Логика
конструирования уравнений Шредингера:
Логика
конструирования уравнений Шредингера:
![]() -
волновой процесс;
-
волновой процесс;
![]() -
использование мировых констант;
-
использование мировых констант;
![]() -
линейные и однородные по(необходимость удовлетворения принципу
суперпозиции - интерференция и дифракция);
-
линейные и однородные по(необходимость удовлетворения принципу
суперпозиции - интерференция и дифракция);
![]() -
волна де Бройля – одно из его решений;
-
волна де Бройля – одно из его решений;
![]() -
существуют
-
существуют![]() .
.
Отсюда

уравнение Шредингера для p=const(для волнового процесса сP=const(волна де Бройля).
![]()
Т.к.
![]() ,
то введем силовые поляU(r).
,
то введем силовые поляU(r).
Тогда
получим
![]() - уравнение Шредингера, описывающее
- уравнение Шредингера, описывающее
волновую функцию в потенциальном поле U(r).
При
этом
![]() - однозначны, конечны, непрерывны в
точках и линиях разрыва;
- однозначны, конечны, непрерывны в
точках и линиях разрыва;![]() - собственные значения,
- собственные значения,![]() - собственная функция.
- собственная функция.
Стационарные состояния и уравнение Шредингера для стационарных состояний
Выберем
, стремящуюся к![]() ;
цель – убрать для*
зависимость отt.
;
цель – убрать для*
зависимость отt.
Тогда
f(t).
Подставим![]() в уравнение Шредингера и с учетом полной
энергии частицы
в уравнение Шредингера и с учетом полной
энергии частицы![]() ,
получаем уравнение Шредингера для
стационарных состояний:
,
получаем уравнение Шредингера для
стационарных состояний:
![]() - удовлетворяет принципу суперпозиции.
- удовлетворяет принципу суперпозиции.
Однако, если
![]() два
стационарных состояния, то отсюда не
следует, что
два
стационарных состояния, то отсюда не
следует, что![]() также
описывают стационарное состояние.
также
описывают стационарное состояние.
Г. Движение электронов в твердых телах (зонная теория)
1. Так
как
![]() ,
(казиимпульс и квазивектор), то решения
ищем в виде функций Блоха:
,
(казиимпульс и квазивектор), то решения
ищем в виде функций Блоха:
![]()
![]()
Система обладает инвариантностью сдвига только на векторы решетки.
2.
Нахождение энергетического спектра
электронов в кристаллах.![]()
![]()
для одной степени свободы.
Для N атомов:

а)
M>>m
(адиабатное приближение):
![]()
Для
электронов:

Для
ядер:

Здесь Е - энергия электронов, движущихся в поле малоподвижных ядер,
- полная энергия кристалла.
б) Одноэлектронное приближение.
![]() - постоянное усредненное поле от всех
электронов.
- постоянное усредненное поле от всех
электронов.

Тогда
![]() .=
-E
.=
-E
![]() -Это
одноэлектронное уравнение Харти-Фока.
-Это
одноэлектронное уравнение Харти-Фока.
Решение одноэлектронного уравнения:
![]() ,
каждое из
,
каждое из![]() удовлетворяет этому уравнению.
удовлетворяет этому уравнению.
Исследуем его решение для одного электрона.
Т.к. для изолированного атома,
то запишем зависимость U(r) в виде функции меандра – модель Кронига – Пени:
 гдеc=a+b– период решетки.
гдеc=a+b– период решетки.
Замечание
:член в виде![]() не учитывает принципа Паули.
не учитывает принципа Паули.
Поправим уравнение Харти-Фока: представим одноэлектронную волновую функцию в первом квантовом состоянии в виде:
![]()
В результате полная волновая функция системы электронов с учетом суперпозиции Паули может быть записана в виде:

Рассмотрим энергию электрона при E<U*.
Имеем
![]()
V(r) - потенциальная энергия взаимодействия электрона с ядром,
(r) – потенциальная энергия взаимодействия электрона с полями всех электронов.
Заметим: у нас одно уравнение с тремя неизвестными – E,,K.
Как
же быть? Исходя из изложенных выше
физических представлений следует, что
разумно искать в
виде![]() .
.
Тогда
для таких граничных условий по
![]() ,
подставив
,
подставив![]() в уравнение Шредингера, имеем:
в уравнение Шредингера, имеем:
![]()
и для
![]() получаем:
получаем:
![]()
Отсюда получаем:
0<x<a:
![]() ;
;
a<x<(a+b):
![]() .
.
Постоянные
A,B,C,Dвыбираем так, чтобы![]() были непрерывны при r=0 иr=a,
и чтобы
были непрерывны при r=0 иr=a,
и чтобы![]() .
.
Имеем: A+B=C+Dприr=0 сшили U(r).

Система имеет решение, если детерминант матрицы, состоящей из коэффициентов системы равен нулю.
Отсюда
![]() .
.
Перейдем
к пределу:
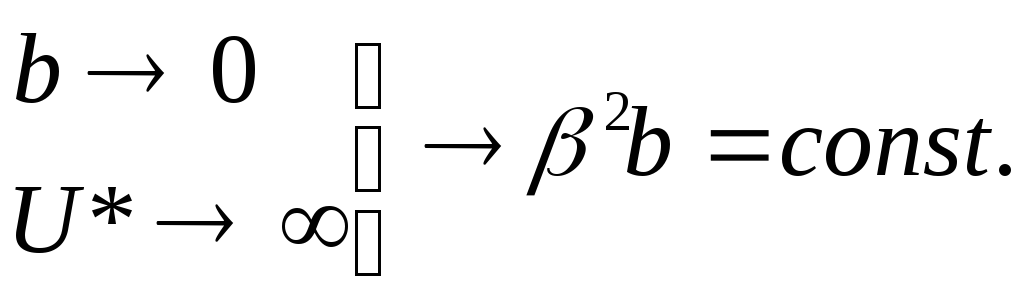
Точнее: (физический смыслp–
вероятность туннелирования электрона
(физический смыслp–
вероятность туннелирования электрона
через барьер).
Тогда
![]() (*)
(*)
Итак:
![]() будет удовлетворять (*) и исходному
волновому уравнению, если (*) будет иметь
решения относительно.
будет удовлетворять (*) и исходному
волновому уравнению, если (*) будет иметь
решения относительно.
Решим графически:
Методика решения: Возьмем (a,k)1, находимcos(ak1), точки пересечения линии, параллельной (0,a) дают абсциссы, являющиеся корнями (*), соответствующими…данному (ak)1. Так какcos(ak)=1, то левую часть надо рассматривать между двумя параллельными линиями. Из точки пересечения опускаем перпендикуляр и находим совокупность корней.
Т.е. получили дисперсионное соотношение E=f(k) для решетки с периодом ,a.
Если p<1, то запрещенные области уменьшаются, а разрешенные зоны растут.
Если
p>>1(случай
сильной связи электронов со своими
атомами), то ширина запрещенной зоны
увеличивается, а![]() уменьшаются, пока в пределе не превращаются
в точки (дискретные уровни изолированных
атомов)здесь
уменьшаются, пока в пределе не превращаются
в точки (дискретные уровни изолированных
атомов)здесь![]() .
.
Если p0(слабая связь), то (*)cos(ka)=cosa, т.е. запрещенных зон нет, приближаемся к случаю электронного газа в кристалле (к случаю металла).

при p0 (Uмедленнее, чемb0), прозрачность барьера растет.
Исходя
из анализа p=(0,),
граница допустимых значений(а значит Е) соответствует дляkзначениям![]() .
.
Вспомним:
Т.е.
диапазон предельных значений соответствует
![]() А
т.к.
А
т.к.![]() k=
k=![]() .
.
Получили дисперсионное соотношение для p=3/2:
Трехмерная ситуация:
![]() ,
,
полная
волновая функция одного электрона -
![]() ,
,
если переменные в уравнении Шредингера разделяются.
Если p>>1:

Если
ячейки кубические:
![]() то
то![]()
т.к.
![]() ,
то
,
то![]()
Т.е.
![]() сопоставляется с неким импульсом
(квазиимпульсом) электронов в зоне
(вспомним, для свободной частицы
сопоставляется с неким импульсом
(квазиимпульсом) электронов в зоне
(вспомним, для свободной частицы![]() ).
Т.к. для электронов
).
Т.к. для электронов![]() ,
то
,
то
![]()
![]()
![]() .
.
Замечание:
В
случае эксперимента с рентгеновскими
лучами n=2asin![]() – условие Вульффа-Брега для отражения
рентгеновских лучей от кристаллической
плоскости.
– условие Вульффа-Брега для отражения
рентгеновских лучей от кристаллической
плоскости.
По аналогии с этим, границы запрещенной зоны можно определить из условия отражения электронных волн от кристаллических плоскостей. Тогда

![]() - границы.
- границы.
Т.е. область значения k, при которыхE(k) изменяется непрерывно, а на границах терпит разрыв – называетсязоной Бриллюэна.
![]() - первая зона Бриллюэна.
- первая зона Бриллюэна.
Т.е.
периодичность системы приводит к тому,
что состояния электрона с kи![]() физически неразличимы, то нет необходимости
рассматриватьE(k)
во всех зонах Бриллюэна.
физически неразличимы, то нет необходимости
рассматриватьE(k)
во всех зонах Бриллюэна.
E(k’)=E(k),
где![]() Т.е.сводим к первой
зоне, меняяn(вторая зона
–n=1, третья зона – возьмемn=2, и т.д.). ИзображениеE(k) в области
Т.е.сводим к первой
зоне, меняяn(вторая зона
–n=1, третья зона – возьмемn=2, и т.д.). ИзображениеE(k) в области![]() для всех зон называетсяприведенной
зоной Бриллюэна.
для всех зон называетсяприведенной
зоной Бриллюэна.
В
трехмерном случае при приведении зон
вводятся векторы обратной решетки
![]() так,
чтобы выполнялось условие:
так,
чтобы выполнялось условие:![]() ,
где
,
где

Дефекты в кристаллах.
1). Пусть в узле r* существует дефект. Тогда:U(r*)=U(r)+U*. В зависимости от величины отношенияU*/Uуровни глубокие либо мелкие. Результат-в зоне запрещенной появяться локализованные разрешенные состояния,Et.
(а). Если Et<<kT, то притмесь легирующая(если электрон эмиссируется в зону С – то лок. центр является донором, если электрон захватывается из зоныV– акцептор).
2). Классификация дефектов:
точечные (n=0),-вакансии и дефекты внедрения;
линейные (n=1),-дислокации;
плоские (n=2),-границы кристаллитов;
объемные (поры и трещины).
3).
Энергия ионизации атома:
![]() .
Эта оценка следует из условия устойчивости
атома в рамках квазиклассических
рассуждений:
.
Эта оценка следует из условия устойчивости
атома в рамках квазиклассических
рассуждений:![]()
Действительно:
условие устойчивости атома mv2/r=Ze2/r2;mvr=n![]() ;
Тогда кинетическая энергия электронаE=mv2/2=me4Z2/2
;
Тогда кинетическая энергия электронаE=mv2/2=me4Z2/2![]() 2n2;
приn=1 получаем выражение
для энергии ионизации атома:
2n2;
приn=1 получаем выражение
для энергии ионизации атома:
![]() .
.
Заметим, из-зп поляризации среды энергия ловушки (энергия ионизации стороннего атома) равна:
![]() .
.
4). Примесная зона:
Пусть Ntчисло атомов в одном см3. Тогда расстояние между атомамиan=(Nt)-1/3. Еслиao – радиус первой боровской орбиты свободного атома водорода (ao=0,53 А), то:
а=ao![]() -радиус электронной орбиты
водородоподобного атома.
-радиус электронной орбиты
водородоподобного атома.
Перекрытие волновых функций произойдет тогда, когда an=a. Отсюда:
an=(Nt)-1/3
= a = ao![]() .Значит: для перекрытия волновых
функций неоходимо произвести легирование
материала до концентраций:
.Значит: для перекрытия волновых
функций неоходимо произвести легирование
материала до концентраций:
Nt=
Например, для арсенида галлия Nt> 1024(0,07/10)3~4.1019см-3.
