Глава 2

Простейшие стационарные процессы теплопроводности

§ 2.1. Cлучаи тонкой пластины

Тонкие пластины- это такие пластины, на процессы в которых не влияют края (рис.2.1), т.е.

 < 0,1 h;

2l_возм << h,

t_c1, t_c2 - температуры на поверхностях ("стенка 1", "стенка 2").

Примеры тонких пластин:подложкодержатели, кремниевая пластина, стена здания, стенка холодильника и другие.

Задачи тонкой пластины в различных условиях однозначности

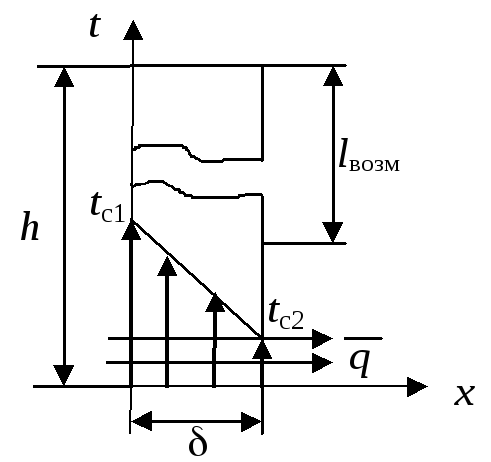
Задача 1. Определить стационарное поле температурыt(x, ) и тепловую нагрузку qтонкой пластины без внутренних источников тепла для граничных условий 1-го рода,  = const (рис.2.2). Толщина пластины, коэффициент теплопроводности.

Рис.2.2.

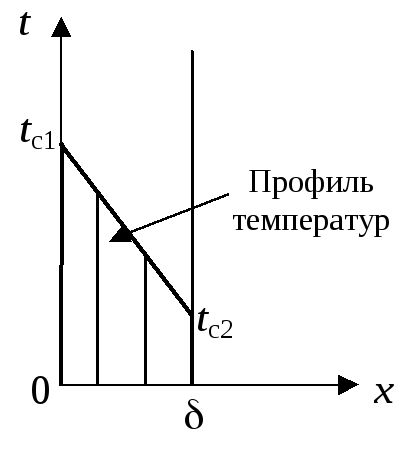
Рис.2.1.

Решение:

Найдем тепловую нагрузку q:

;

,

где q- тепловая нагрузка;- температурный напор;R_терм- внутреннее термическое сопротивление.

Проведем приведение к безразмерным величинам, которое дает:

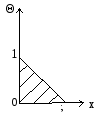
а) общий результат для всех подобных процессов (всех плоских тонких пластин);

б) экономию в эксперименте.

Приведение к безразмерному виду результата расчета профиля температуры:

1) переходим к разностным температурам:

;

2) делим разностный температурный профиль на известную разность температур (температурный напор), в данном случае это .

или ,

где - безразмерная температура;х- безразмерная координата,Х=х/.

Для выражения в безразмерном виде легче поставить эксперимент, а эксперимент необходим тогда, когда мы не можем проинтегрировать задачу.

З

Рис.2.3.

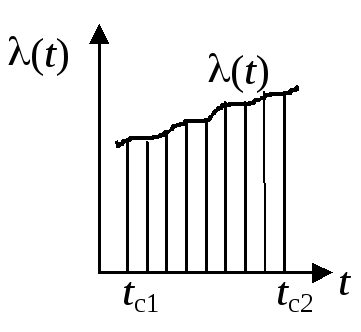
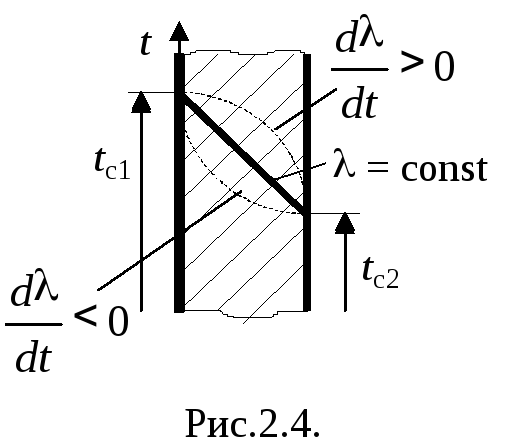
адача 2.Решим задачу 1 при условии, что = (t) (рис.2.3):

;

;

,

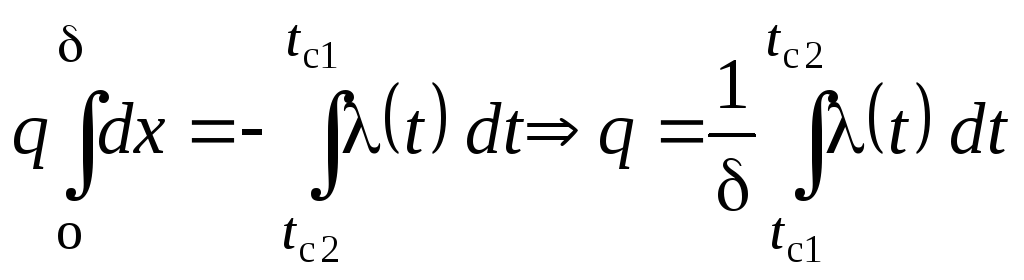где .

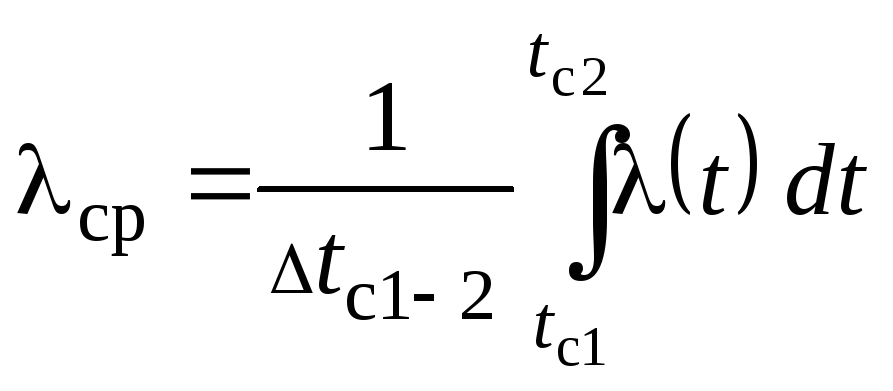Если (t) = a + bt, то_{ср. инт}= _{ср. арифм}и профиль температуры внутри пластины может иметь вид, отличный от прямолинейного (рис.2.4).

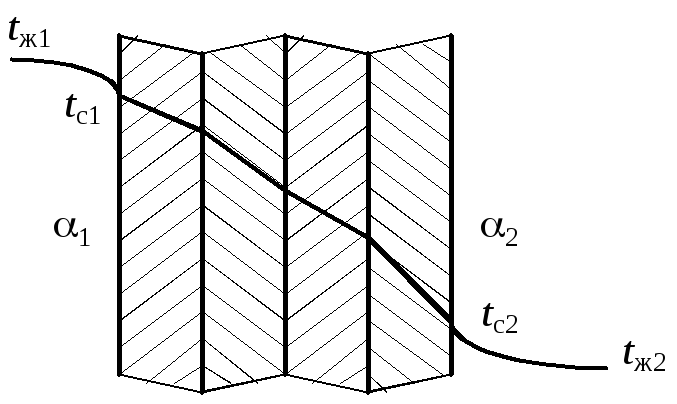
Задача 3.Определить стационарную тепловую нагрузкуq тонкой пластины, которая разделяет холодную и горячую среды или жидкости, т.е. в граничных условиях 3-го рода (рис.2.5).

Задано:, , t_ж1,t_ж2, ₁, ₂.

Найти:q, t_c1, t_c2.

q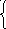=₁ ( t_ж1 – t_c1) - по закону Ньютона-Рихмана;

q = / (t_c1 – t_c2) - из задачи 1;

q = ₂ (t_c2 – t_ж2) - по закону Ньютона-Рихмана.

Рис.2.5.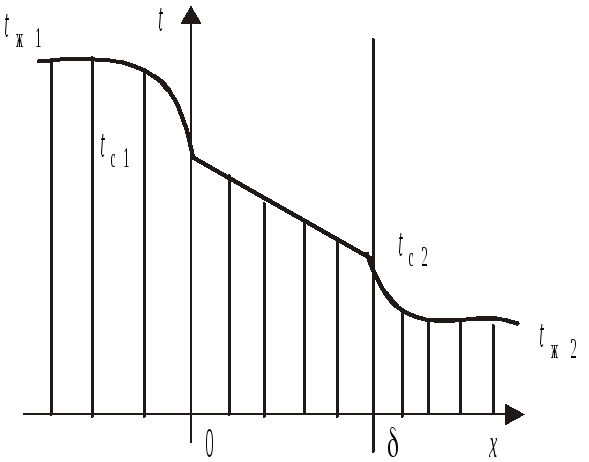

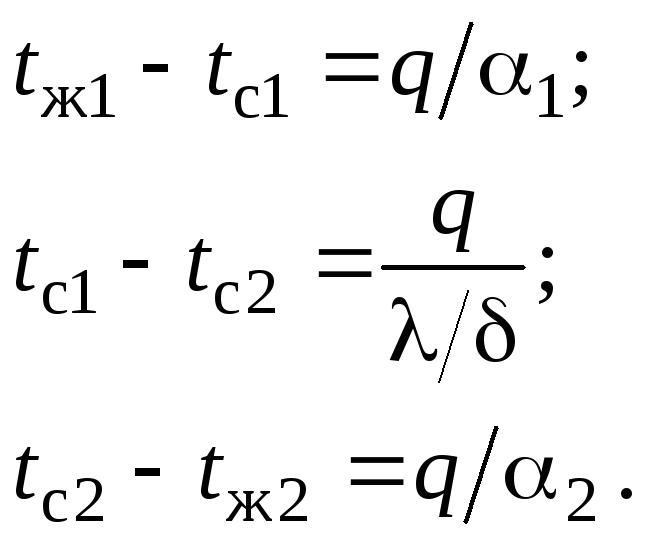
После сложения трех уравнений

;

;

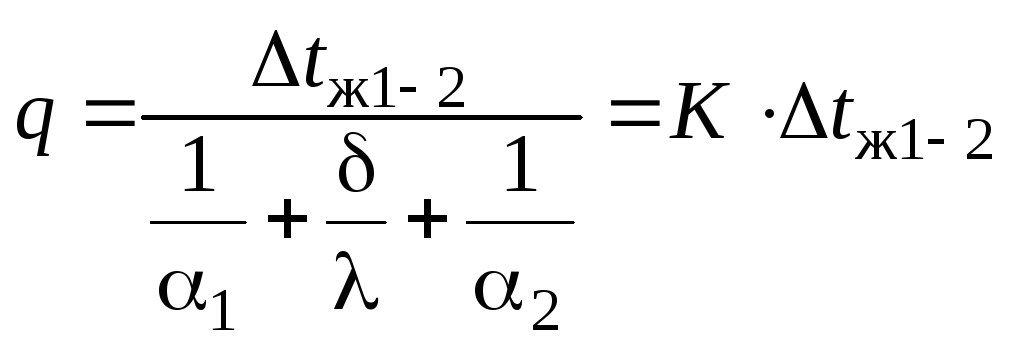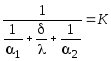- коэффициент теплопередачи [Вт/м²С], гдеKхарактеризует интенсивность теплопередачи между горячими и холодными жидкостями через твердое тело (в отличие от- коэффициента теплоотдачи).

Задача 4. Определить стационарную тепловую нагрузкуq пакета тонких пластин, имеющих идеальный контакт друг с другом (граничные условия 4-го рода) (рис.2.6).

Рис.2.6.

Дано:₁, ₂,... _n; ₁, ₂, _n.

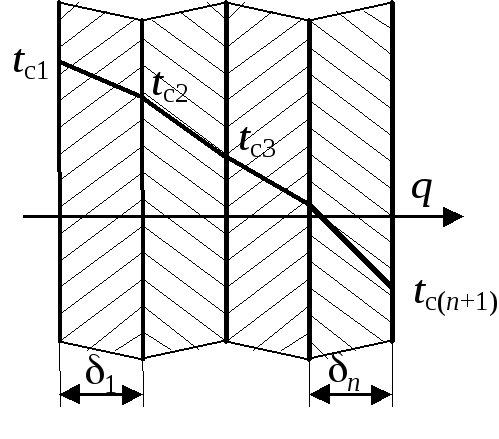
Найти:q, t_ci.

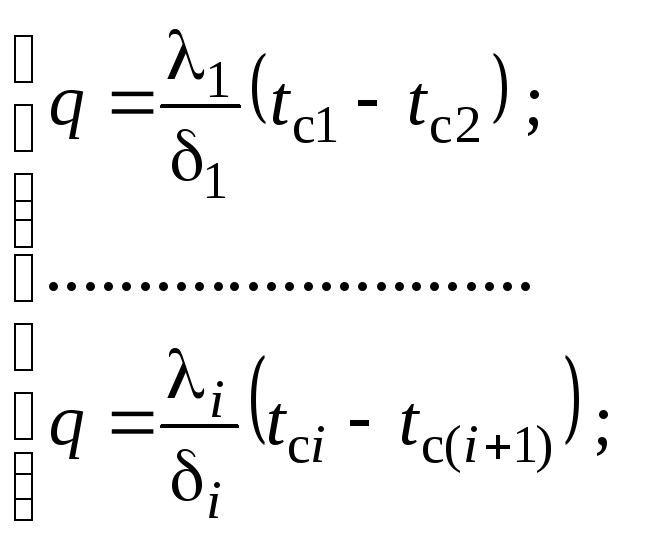
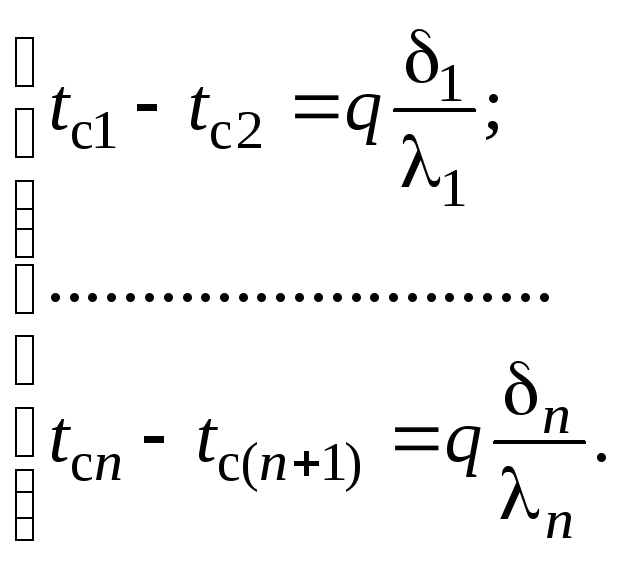
После сложения уравнений

Рис.2.7.

Для граничных условий 3-го рода (известны t_ж1 иt_ж2- температуры внутренней и внешней среды, а температурастенок неизвестна) получаем решение в виде (рис.2.7):

,

где - внешние термические сопротивленияR_внешн;- сумма внутренних термических сопротивлений пластин.

З

Рис.2.8.

адача 5.Определить стационарную тепловую нагрузку тонкой пластины, которая разделяет горячую и холодную жидкости. На одной стороне пластины установлены ребра (рис.2.8).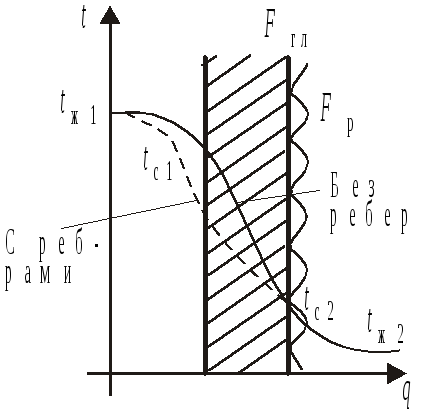

Дано:, ,t_ж1, t_ж2 , ₁, ₂ ,F_гл , F_p(F_гл,F_р- площадь гладкой и ребристой поверхности).

Найти:q_гл, Q_p.

;

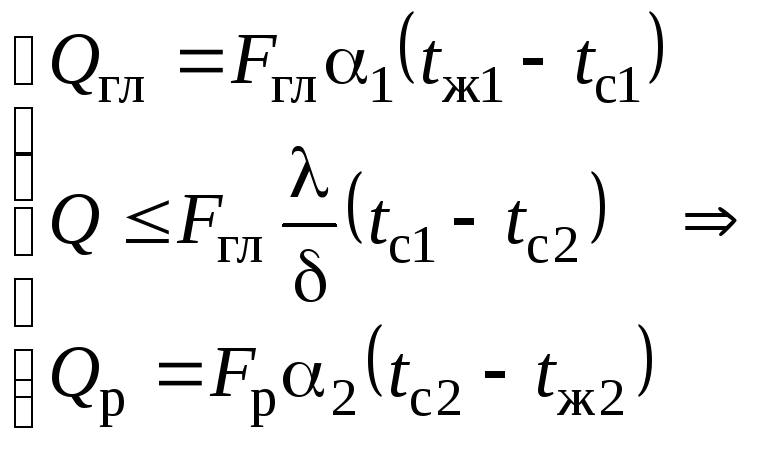
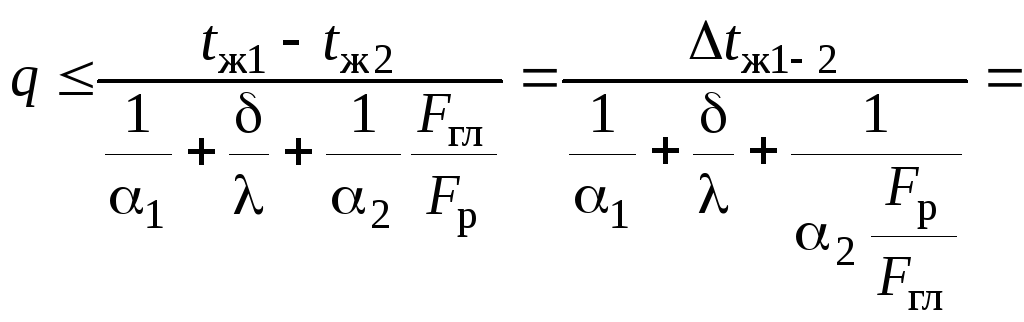
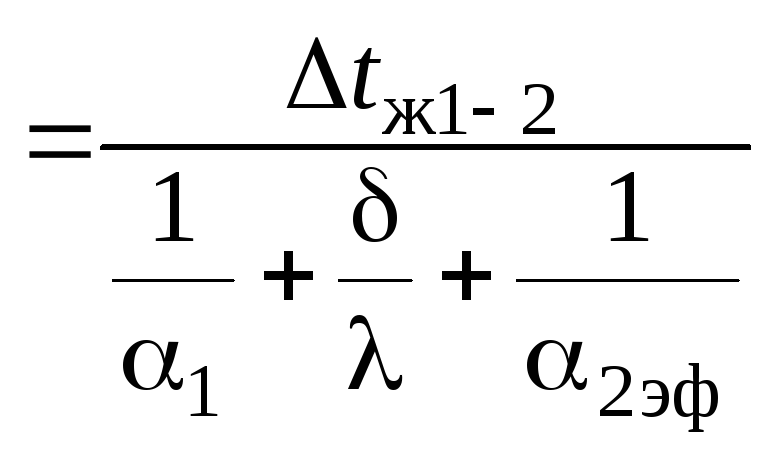
сравнить с решением задачи 3 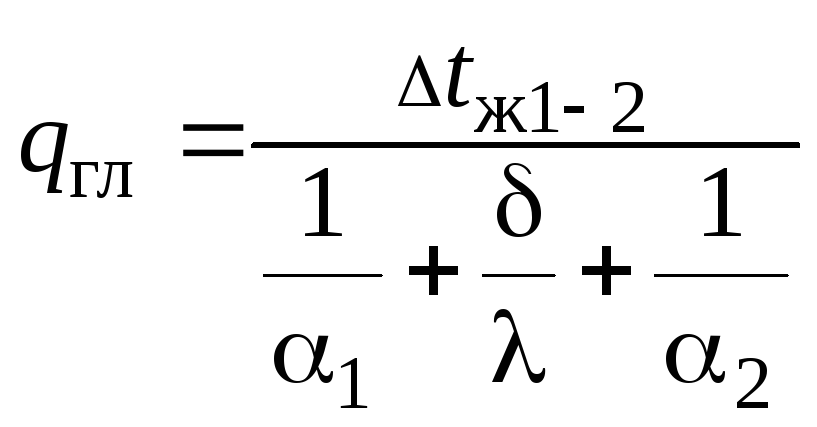; - коэффициент оребрения всегда больше единицы. Peбра устанавливаются там, где коэффициент теплопроводности маленький, - эффективный коэффициент теплоотдачи.

Задача 6. Определить стационарное поле температуры в тонкой пластине, на поверхности которой заданы граничные условия 1-го рода, а внутри действуют внутренние источники тепла q_v  0 (рис.2.9).

Рис.2.9.

Дано: , , t_c1 > t_c2, q_v.

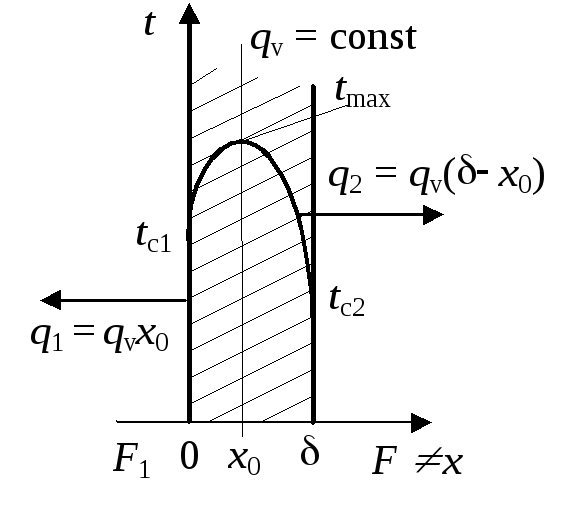
Найти: t(x), t_max , x₀ ,(dt/dx)_{наиб x =  - 0}

q₁, q₂ - плотность теплового потока на поверхности F₁ и F₂.

; ;

;

; ;.

Перейдем к безразмерным величинам.

,

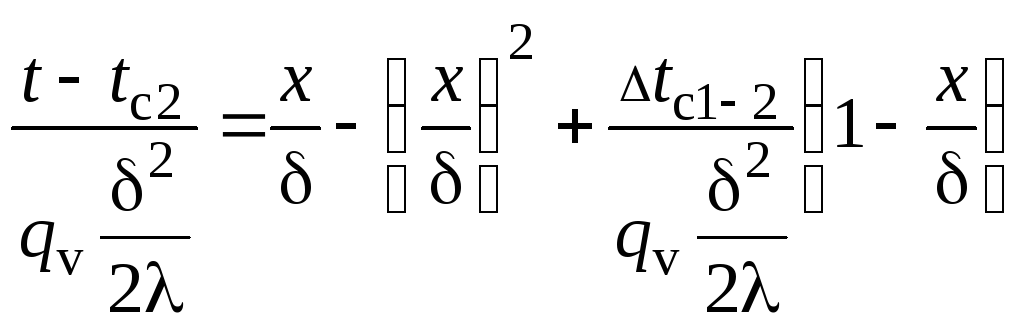где ;;;

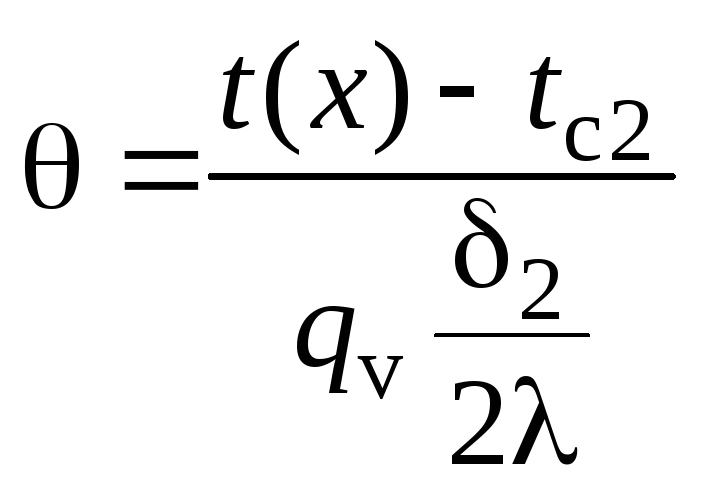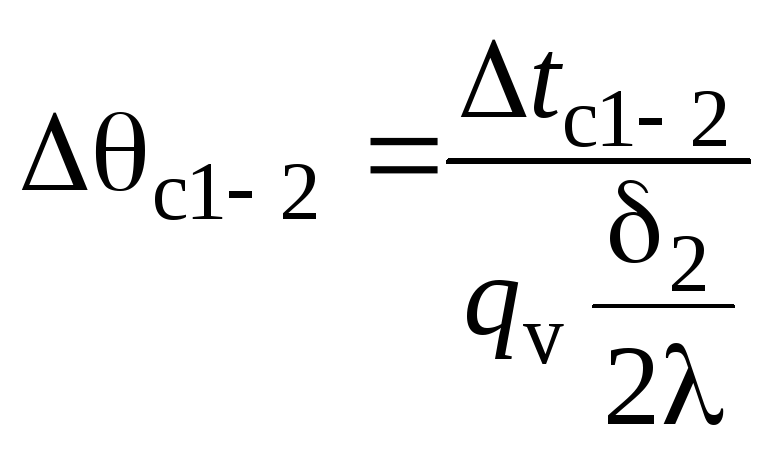Рис.2.10.

Рис.2.11.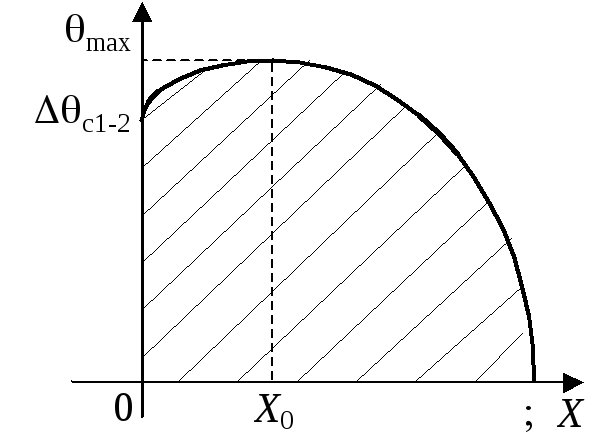

- результаты для поля температуры в плоской пластине с внутренним источником тепла в безразмерном виде (рис.2.10).

Найти _max:

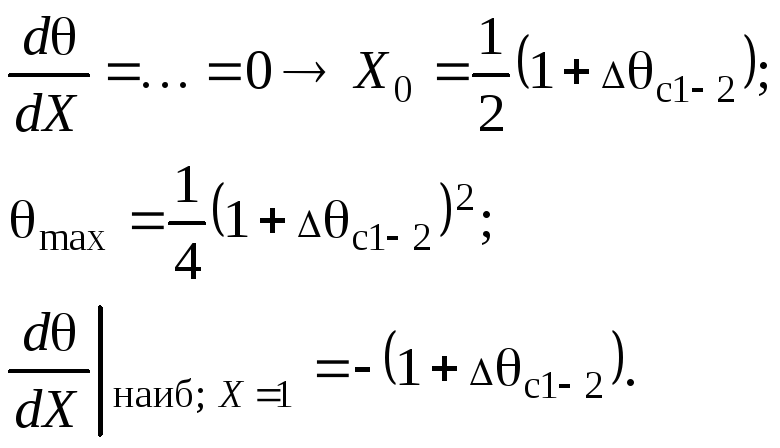
а) Симметричный случай - пластина охлаждается с обеих сторон равномерно (рис.2.11).

; ;;;

Рис.2.12.

; .

б) Случай абсолютной асимметрии при условии Х₀ = 0, т.е. максимум температуры на 1-йгранице, где(рис.2.12). Тогда;;.

Отсюда следует: q₁ = 0;

;

так как 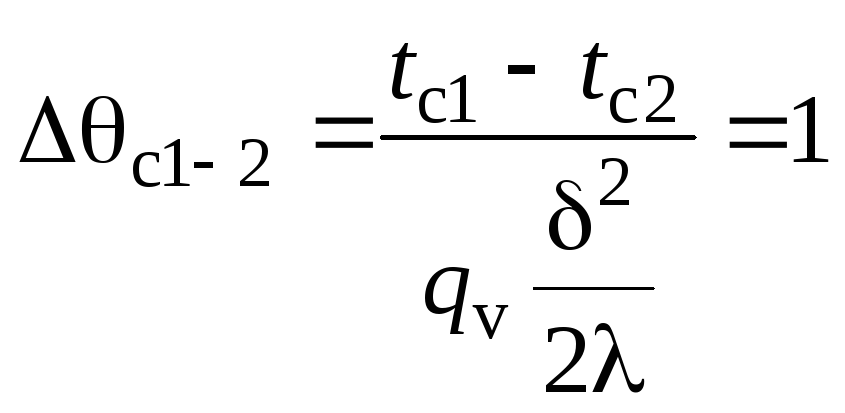, то- условие абсолютной асимметрии.

Задача 7.Найти стационарное поле температуры в тонкой пластине при наличии внутренних источников тепла и симметричных граничных условий 3-го рода (рис.2.13).

Рис.2.13.

Дано: t_ж, , 2₀, , q_v.

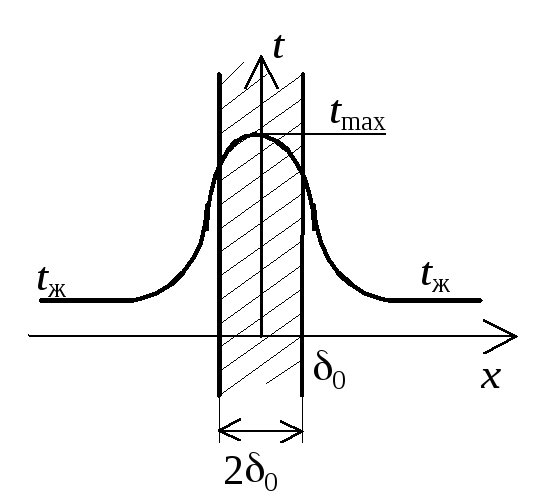
Найти: t(x).

.

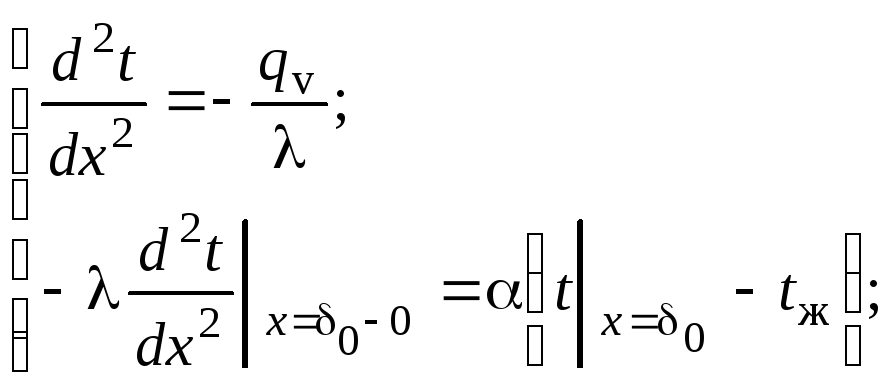
Приводим решение в безразмерном виде: 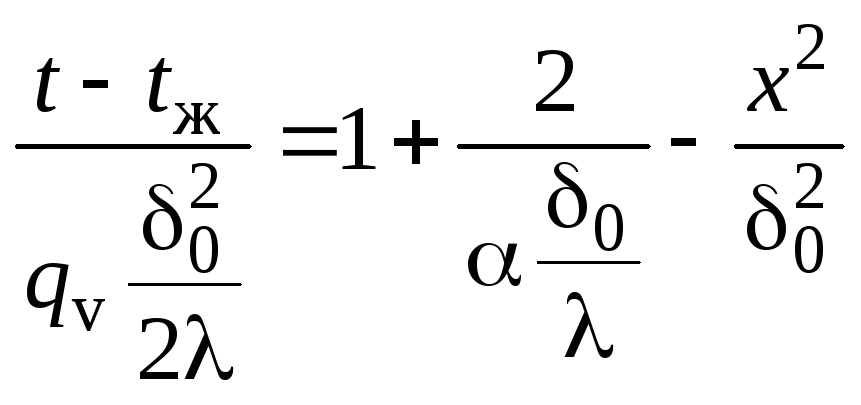- решение задачи.

Обозначим . Bi - число Био. Физический смысл Bi - мера отношений термических сопротивлений системы "пластина - среда".

.

Построим поле t в безразмерном виде (рис.2.14):

а) Bi = 0,1- можно пренебречь полем температуры внутри тела:= 21 –Х²;

б) Bi = 1 - нельзя пренебречь полем температуры внутри тела:= 3 –Х²;

в

Рис.2.14.

) Bi = 10- весь перепад температуры внутри тела: = 1,2 –Х².