Лекция №7.

H=U+pV энтальпия, так же как и внутренняя энергия – функция состояния.

рV – функция состояния, т.о. энтальпия.

Н – функция состояния, т.е. изменения не зависят от пути проведения процесса.

Вывод: в двух случаях при p=const, V=const, когда все полезные виды работ равны 0, теплота Q (Q_p и Q_V) приобретает свойства функции состояния.

Итоги: первое начало т/д для закрытых систем:

dU=U-A

А – различные виды работ

A=pdV+OA’

А’ – полезные работы, не связанные с изменением объема

A’=dS+dl+…

p, dV, , dS, , dl – параметры, характеризующие систему.

Этот переход возможен при равновесном процессе(если не равновесный, то p, dV – относятся к внешней среде).

Внутренняя энергия: (T, V, p)=0;

T – характеристика кинетической энергии;

V – определяет потенциальную энергию частиц;

U=(T,V).

Запишем дифференциал и при протекании процесса:

Э нтальпия: функция теплоты и давления H=(T,P)

H=U+pV.

При постоянстве давления и отсутствии других видов работ теплота …. изменением энтольпии системы.

При V=const, и отсутствии вообще всех работ, теплота определяется изменением внутренней энергии

U, H – функции состояния системы, экстенсивные, не известны абсолютные значения.

Взаимосвязь между изменениями функций ∆U и ∆H.

∆Н=U-p∆V+V∆p

При p=const ∆H=∆U+p∆V.

При V=const ∆H=∆U+v∆p.

Для химической т/д наиболее интересными процессами являются химические реакции, допустим что в химической реакции температуры исходных и конечных веществ подчиняется уравнению идеального газа:

∆(pV)=∆n₁-RT

∆n – изменение числа молей газообразных веществ, участвующих в химической реакции.

∆M_T=∆U_T-∆n_ГRT ()

Если в химической реакции участвуют на ряду с газообразными жидкие или твердые вещества, то при условии n_Г0, изменение величины ∆(pV) для конденсированных веществ можно пренебречь ∆(pV)0, то  имеем опять ().

Если реакция протекает либо в твердом теле либо в жидкости, т.е. в конденсированной среде, слагаемое ∆n_ГRT=0, а значение изменения внутренней энергии приблизительно равно ∆Н, т.е. ∆Н∆U.

Теплоемкость газа.

В общем случае теплоемкость вещества – функция процесса. Запишем определение теплоемкости математически:

И

A=0

спользуя следствие первого начала т/д:

X

A’=0

предполагает отсутствие каких либо работ

О

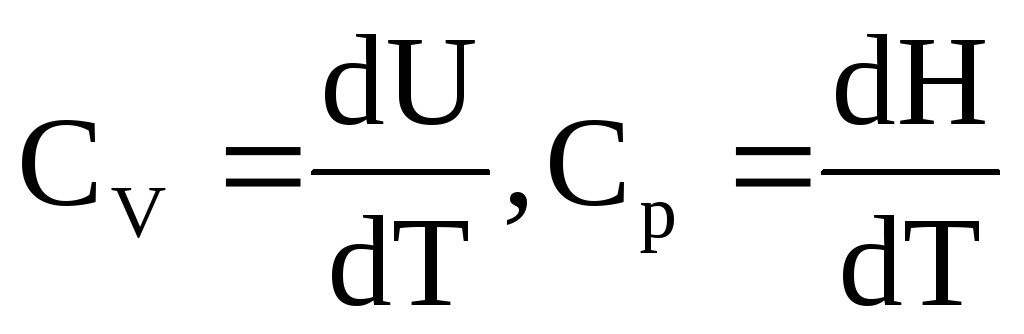
– функции экстенсивные

ба состояния справедливы для любых веществ в любых агрегатных состояниях

n – число молей

Н

()

айдем взаимосвязь между C_p и C_V.

П

dU=(T,V)

()

ервое слагаемое этого выражения представляет собой изменение внутренней энергии при постоянном давлении, а надо найти ( …. (dT) при V=const).

И спользуя уравнение состояния: (T,P,V)=0. Запишем полный дифференциал объема:

– подставим это выражение в формулу для dU()

V=(T,p).

П осле преобразований получим выражение:

У читывая взаимосвязь a

З

Подставив это уравнение в исходное выражение C_p ()

акрепляя давление p=const

П

()

ервый член в этом выражение учитывает изменение внутренней энергии в следствии расширении тела и произведенной работы против внутренних сил, второй определяет работу расширения против внешних сил при нагревании на 1^оС при p=const.

П рименим формулу () к идеальным газам.

В

 в выражение () первое слагаемое отсутствует

идеальном газе U=(T).

Уравнение Майера

С_p-С_V=R

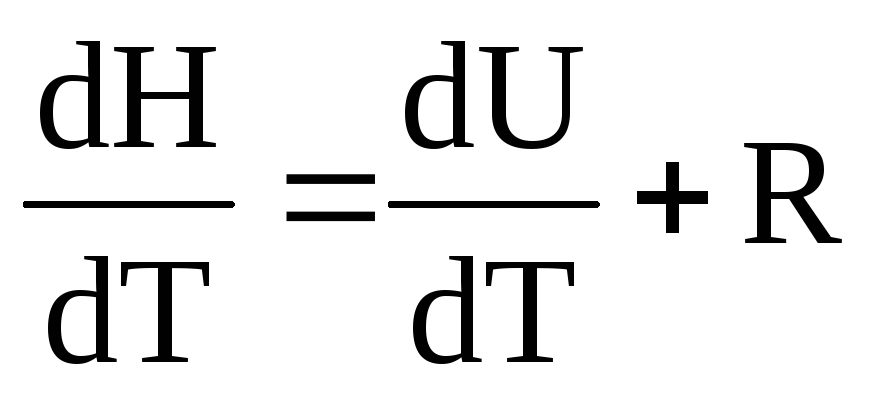H=U+PV

C_p-C_V=R

Определим теплоемкость одноатомного идеального газа.

Т .о. при p=const и V=const теплоемкость идеального газа не зависит от температуры.

C_p=a+bT+cT²+dT³+…+T^-2

Обеспечивает стыковку теплоемкости в области высоких и низких температур.

4. Адиабатический процесс.

Q=0

- dU=A или после интегрирования

В таком процессе работа производится только за счет изменения внутренней энергии, следовательно температура системы при адиабатическом процессе работа и изменение внутренней энергии равны, но имеют разные знаки. Для идеального газа: dU=n_*C_V*dT, поэтому величина работы будет равна:

П олучим уравнение адиабаты: для этого используя уравнение состояния нужно в выражении работы заменить давление через объем и проинтегрировать. Удобно при этом выразить газовою постоянную R через разность теплоемкостей (С_P-С_V) и ввести адиабатный коэффициент , который определяется как:

-

проинтегрируем и получим

dU=A; -nC_VdT=pdV

TV^-1=const.

P

Воспользуемся уравнением состояния и выразим T через P и V.

V^=const’