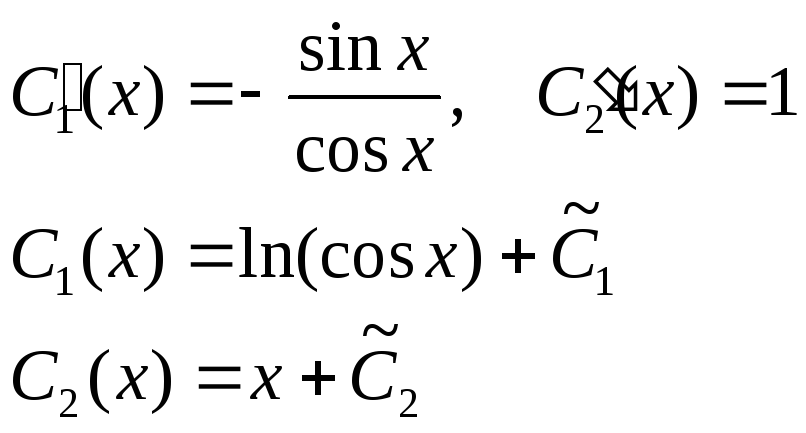диффуры / Дифференциальные уравнения n-го порядка
.doc
Дифференциальные уравнения n-ого порядка.
![]() (1)
(1)
![]() (2)
(2)
Если уравнение разрешимо относительно старшей производной то имеет вид (1). Так же уравнение n-го порядка можно представить в виде системы из n уравнений первого порядка.
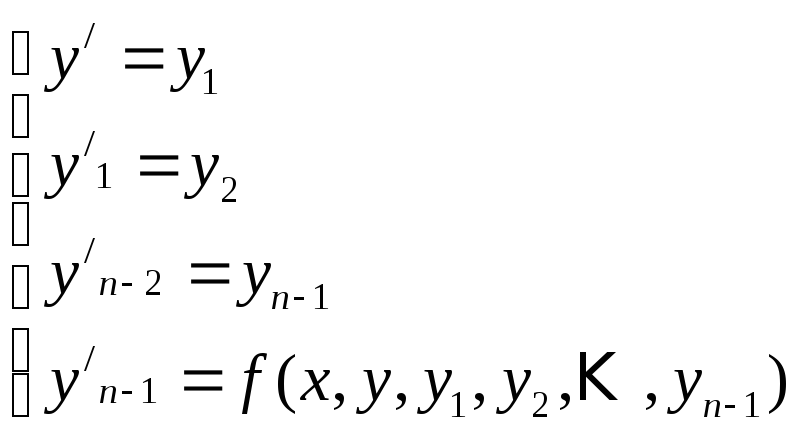 (3)
(3)
Для уравнения n-ого порядка выполнены условия теоремы о существовании и единственности для системы так как (1)~(2)~(3).
Простейшие случаи понижения порядка.
-
Уравнение не содержат искомой функции и ее производной до порядка k-1 включительно, то есть
![]() .
(4)
.
(4)
В
этом случае порядок может быть понижен
до
![]() заменой
заменой
![]() .
Если из этого уравнения выразить
.
Если из этого уравнения выразить
![]() тогда решение y
можно определить k-кратным
интегрируемым функции p.
тогда решение y
можно определить k-кратным
интегрируемым функции p.
Пример.
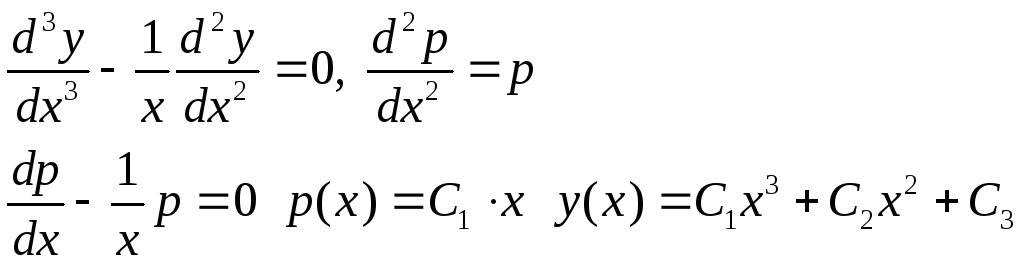 .
.
-
Уравнение, не содержащие неизвестного переменного
![]() (5)
(5)
В
этом случае порядок можно понизить на
единицу подстановкой
![]() .
.
Пример.
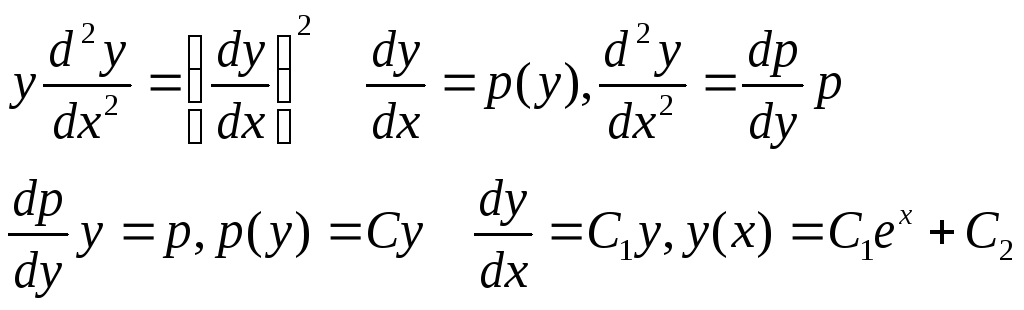 .
.
-
Левая часть уравнения
![]() (6)
(6)
есть
производная некоторого дифференциального
выражения (n-1)-го
порядка.
![]() .
Если
.
Если
![]() -
решение последнего уравнения,
следовательно, существует
-
решение последнего уравнения,
следовательно, существует
![]() .
Мы получили первый интеграл уравнения
(6) и понизили на единицу степень решаемого
уравнения.
.
Мы получили первый интеграл уравнения
(6) и понизили на единицу степень решаемого
уравнения.
Замечание.
Иногда левая
часть (6) становится производной
дифференциального уравнения (n-1)-го
порядка только при умножении на
![]() поэтому здесь могут появиться лишнее
решения (обращающие
поэтому здесь могут появиться лишнее
решения (обращающие
![]() в ноль) или мы можем потерять решение,
если
в ноль) или мы можем потерять решение,
если
![]() разрывная функция.
разрывная функция.
Пример.
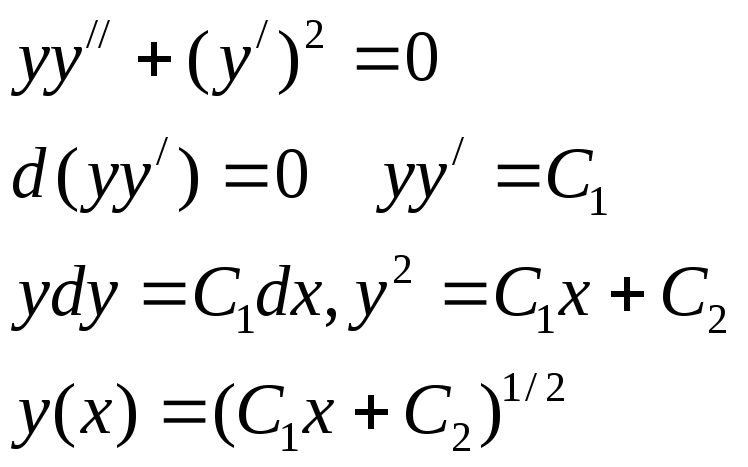
-
Уравнение
![]() (7)
(7)
однородно
относительно
![]() и его производных.
и его производных.
![]() .
.
Или
![]() ,
где показатель
,
где показатель
![]() определяется
из условий однородности.
определяется
из условий однородности.
Порядок
этого уравнения может быть понижен на
единицу заменой:
![]() .
.
Если
подставить эти соотношения в (7) и учесть
однородность функции F
, то в итоге
в получим:
![]() .
.
Пример.
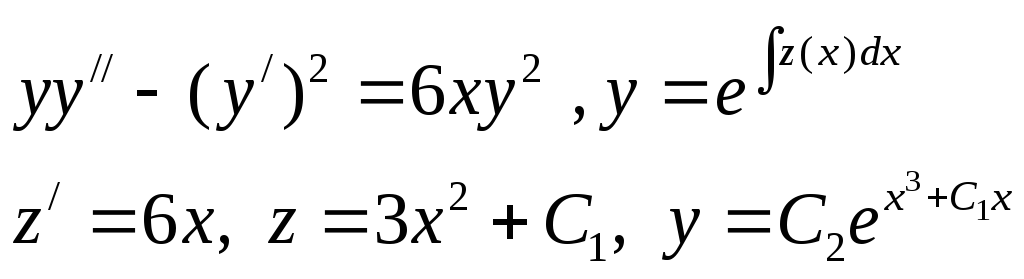 .
.
Дифференциальные уравнения второго порядка,
допускающие понижение порядка.
-
Пусть дано уравнение
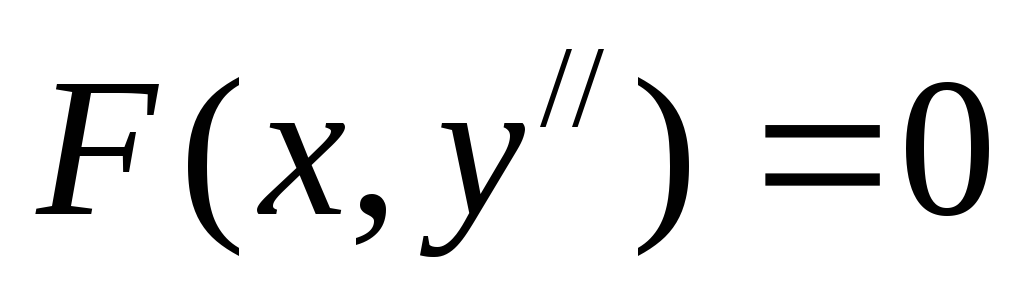 . (8)
. (8)
Подстановка
![]() .
.
Если
уравнение (8) можно разрешить относительно
старшей производной, то уравнение
![]() два раза интегрируется по переменной
x.
два раза интегрируется по переменной
x.
Можно
ввести параметр и заменить уравнение
(8) его параметрическим представлением:
![]() .
Воспользовавшись соотношением для
дифференциалов:
.
Воспользовавшись соотношением для
дифференциалов:
![]() , получаем:
, получаем:
![]() и
и
![]()
II
.
![]() (9)
(9)
Воспользуемся параметрическим представлением:
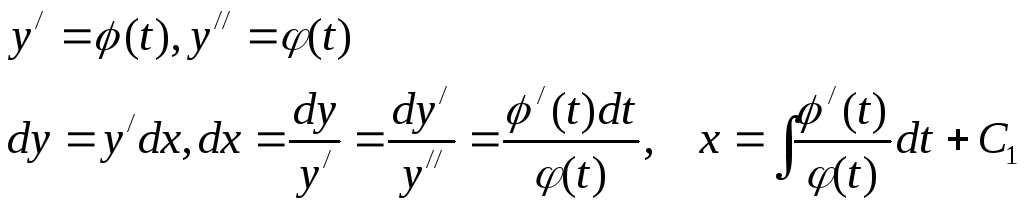
![]()
III.
![]() .
(10)
.
(10)
Понизить
порядок можно заменой:
![]() .
.
Если уравнение (10) разрешимо относительно
старшей производной
![]() ,
то помножим правую и левую часть на
,
то помножим правую и левую часть на
![]() .
Получим:
.
Получим:
![]() .Это уравнение с разделяющимися
переменными:
.Это уравнение с разделяющимися
переменными:![]() .
.
Можно уравнение (10) заменить его
параметрическим представлением:
![]() .
Воспользуемся свойствами дифференциала:
.
Воспользуемся свойствами дифференциала:
![]()
![]() .
.
Пример.
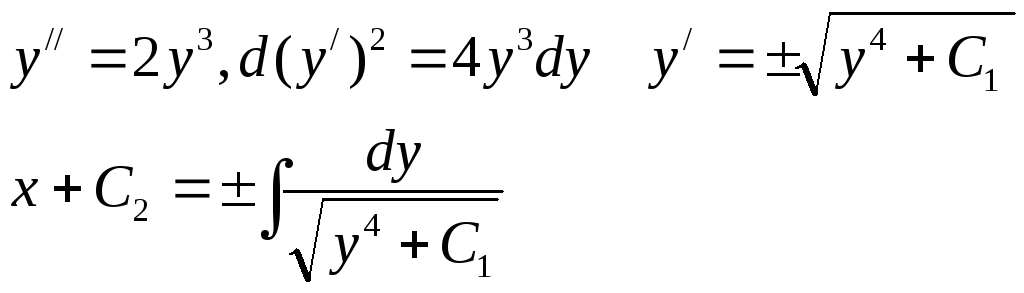 .
.
Линейные дифференциальные уравнения n-ого порядка.
Определение. Линейными
дифференциальными уравнениями n-го
порядка называются уравнения вида:
![]() . (1)
. (1)
Если коэффициенты
![]() непрерывны на
непрерывны на
![]() ,
то в окрестности любых начальных значений
вида:
,
то в окрестности любых начальных значений
вида:
![]() ,
где
,
где
![]() принадлежит интервалу, то в окрестности
этих начальных значений удовлетворяются
условия теоремы о существовании и
единственности. Линейность и
однородность уравнения (1) сохраняется
при любом преобразовании
принадлежит интервалу, то в окрестности
этих начальных значений удовлетворяются
условия теоремы о существовании и
единственности. Линейность и
однородность уравнения (1) сохраняется
при любом преобразовании
![]() ,
где
,
где
![]() - произвольная n раз
дифференцируемая функция. Причем
- произвольная n раз
дифференцируемая функция. Причем
![]() .
Линейность и однородность сохраняется
при линейном и однородном преобразовании
неизвестной функции
.
Линейность и однородность сохраняется
при линейном и однородном преобразовании
неизвестной функции
![]() .
.
Введем линейный дифференциальный
оператор:
![]() ,
тогда (1) можно записать так:
,
тогда (1) можно записать так:
![]() .
Определитель Вронского для
.
Определитель Вронского для
![]() будет иметь вид:
будет иметь вид:
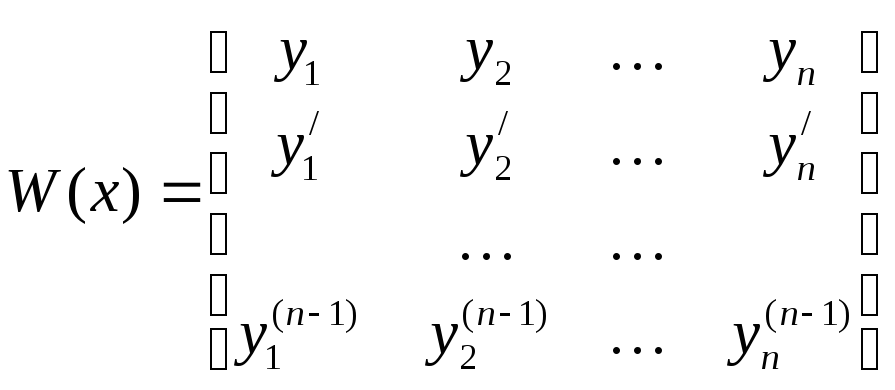 ,
где
,
где
![]() -
линейно независимые решения уравнения
(1).
-
линейно независимые решения уравнения
(1).
Теорема 1. Если линейно независимые
функции
![]() - это решение линейного однородного
уравнения (1) с непрерывными на
- это решение линейного однородного
уравнения (1) с непрерывными на
![]() коэффициентами
коэффициентами
![]() ,
то определитель Вронского
,
то определитель Вронского
![]() не
обращается в ноль ни в одной точке
отрезка
не
обращается в ноль ни в одной точке
отрезка
![]() .
.
( доказывается аналогично случаю системы линейных дифференциальных уравнений)
Теорема 2. Общим решением линейного
однородного уравнения (1) с непрерывными
на
![]() коэффициентами
коэффициентами
![]() будет линейная комбинация решений
будет линейная комбинация решений
![]() ,
то есть
,
то есть
![]() (2), где
(2), где
![]() линейно
независимые на отрезке
линейно
независимые на отрезке
![]() частные решения (1).
частные решения (1).
( доказывается аналогично случаю системы линейных дифференциальных уравнений)
Следствие. Максимальное число линейно независимых решений (1) равно его порядку.
Зная одно нетривиальное частное
решение уравнения (1) -
![]() ,
можно сделать подстановку
,
можно сделать подстановку
![]() и понизить порядок уравнения, сохранив
его линейность и неоднородность.
Обычно эту подстановку разбивают на
две
и понизить порядок уравнения, сохранив
его линейность и неоднородность.
Обычно эту подстановку разбивают на
две
![]() .
Поскольку это линейно однородное
представление, то оно сохраняет линейность
и однородность (1), а значит (1) должно
быть приведено к виду
.
Поскольку это линейно однородное
представление, то оно сохраняет линейность
и однородность (1), а значит (1) должно
быть приведено к виду
![]() .
Решению
.
Решению
![]() в силу
в силу
![]() соответствует решение
соответствует решение
![]() ,
и, следовательно,
,
и, следовательно,
![]() .
Сделав замену
.
Сделав замену
![]() ,
получим уравнение с порядком
,
получим уравнение с порядком
![]() .
.
Лемма.
![]() (3)
(3)
![]() (4)
(4)
Два уравнения вида (3) и (4), где Qi и Pi – непрерывные на [a,b] функции, имеющие общую фундаментальную систему решений, совпадают, т.е. Qi(x)= Pi(x), i=1,2,…n, x[a,b]
На основании леммы можно сделать вывод, что фундаментальная система решений y1 y2 …yn полностью определяет линейное однородное уравнение (3).
Найдем вид уравнения (3), имеющего фундаментальную систему решений y1 y2 …yn . Любой решение y(x) уравнения (3) линейно зависит от фундаментальной системы решений, а это значит, что W[y1 y2 …yn y]=0. Разложим определитель Вронского W[y1 y2 …yn y] по последнему столбцу.
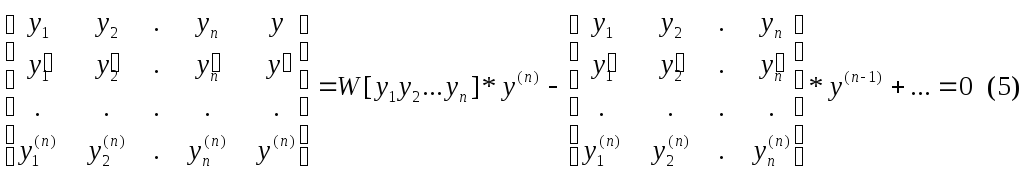
Уравнение (5) является искомым линейным дифференциальным уравнением, имеющим данную систему фундаментальных решений. Мы можем (5) разделить на W[y1 y2 …yn], т.к. он не равен нулю x[a,b]. Тогда:
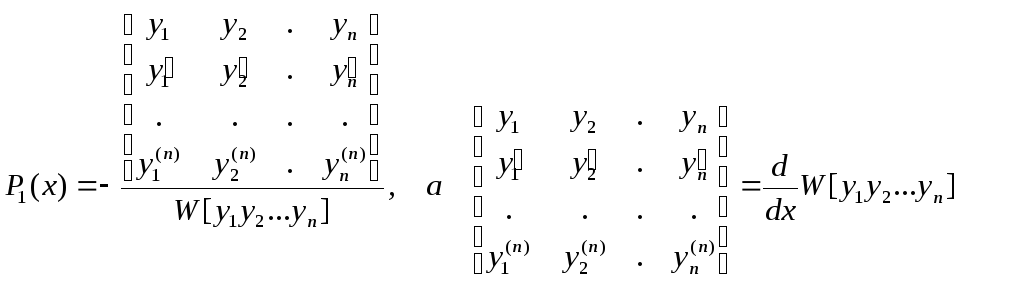 (*)
(*)
По правилу дифференцирования определителя, производная от определителя равна сумме по i=1,2…n определителей, i-ая строка каждого из которых равна производной от i –ой строки исходного определителя. В этой сумме все определители, кроме последнего, равны нулю (т.к. у них по две одинаковые строки), а последний равен (*). Таким образом, получим:
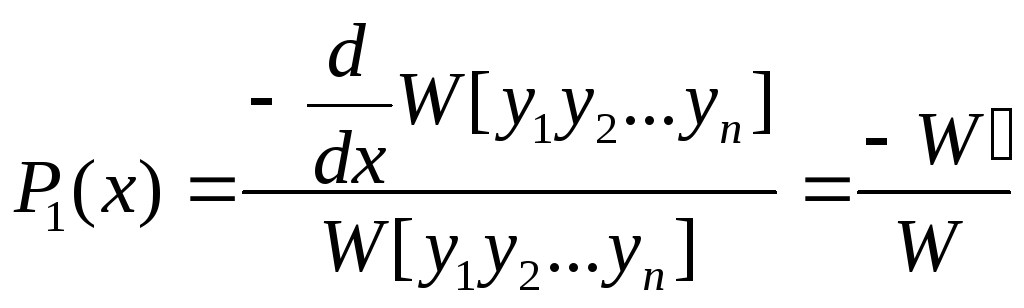 ,
тогда:
,
тогда:
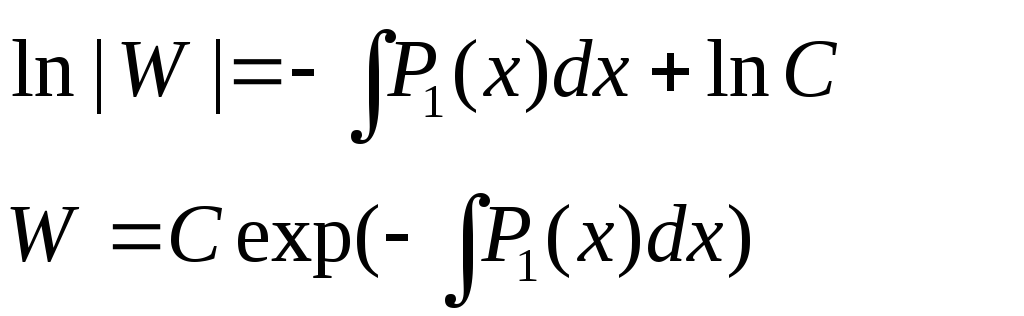 (6)
(6)
![]() (7)
(7)
Определение. Формулы (6) и (7) называются формулами Остроградского-Лиувиля.
Используем (7) для интегрирования линейного однородного уравнения второго порядка. И пусть нам известно одно из решений y1 уравнения (8).
![]() (8)
(8)
Согласно (7) любое решение (8) должно удовлетворять следующему соотношению:
![]() (9)
(9)
Воспользуемся методом интегрирующего множителя.
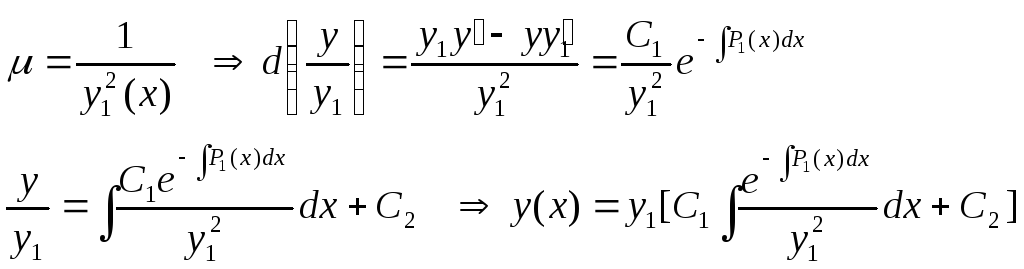
![]()
Линейные однородные уравнения с
постоянными коэффициентами.
Если в линейном однородном уравнении все коэффициенты постоянны,
a0y(n)+a1y(n-1)+….+any=0, (1)
L[y]=0, (2)
то частные решения (1) могут быть определены в виде: y=ekx, где k - постоянная.
a0knekx+a1kn-1ekx+….+an k0ekx=0 a0kn+a1kn-1+….+an=0 (3)
Определение. (3) - характеристическое уравнение.
Вид решения (1) определяется корнями характеристического уравнения (3).
1). Все корни вещественные и различные, тогда:
![]()
2). Если все коэффициенты вещественные, то корни могут быть комплексно-сопряженные.
k1=+i k2=-i
Тогда решения имеют вид:
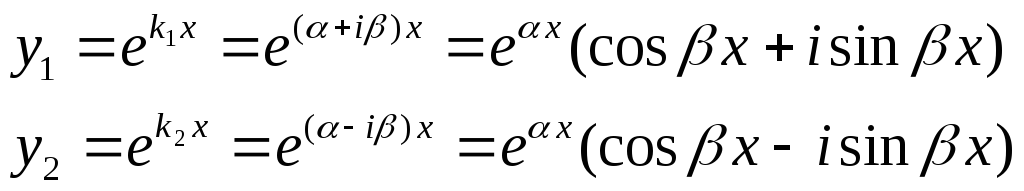
Согласно теореме: если оператор с вещественными коэффициентами имеет комплексно-сопряженные решения, то их действительная и мнимая части также являются решениями. Тогда:
![]()
![]()
Пример.
![]() Решение
представим в виде
Решение
представим в виде
![]() ,
тогда характеристическое уравнение
имеет вид:
,
тогда характеристическое уравнение
имеет вид:
![]()
![]() ,
получим два решения:
,
получим два решения:
![]()
![]() тогда
искомая функция:
тогда
искомая функция:
![]()
3).
Имеются кратные корни: ki
с кратностью i.
В этом случае число различных решений
![]() будет
меньше n,
следовательно, нужно искать недостающие
линейно-независимые решения в другом
виде. Например:
будет
меньше n,
следовательно, нужно искать недостающие
линейно-независимые решения в другом
виде. Например:
![]()
Доказательство:
Допустим,
ki=0,
если подставить его в (3), то получим, что
![]() ,
тогда:
,
тогда:
![]() (4)
(4)
![]() (5)
(5)
![]() -
частные решения (3).
-
частные решения (3).
Пусть
ki0,
сделаем замену
![]() (6)
(6)
Подставим (6) в (1), получим относительно z линейное однородное уравнение n-го порядка с постоянными коэффициентами (7).
![]() (7)
(7)
Корни (3) отличаются от корней характеристического уравнения (7) на слагаемое ki.
![]()
![]()
![]() (8)
(8)
Если
k=ki
, то тогда этому k
соответствует решение уравнения (7) с
корнем p=0
, т.е. соответствуют решения вида z=![]() ,
тогда y=
,
тогда y=![]() -
решение уравнения (1). А общее решение
имеет вид:
-
решение уравнения (1). А общее решение
имеет вид:
![]() решение
для ki
решение
для ki
![]()
Уравнение Эйлера.
Определение. Уравнение вида:
![]() ,
(1)
,
(1)
ai-постоянные коэффициенты, называется уравнением Эйлера.
Уравнение Эйлера заменой x=et сводится к линейному однородному уравнению с постоянными коэффициентами.
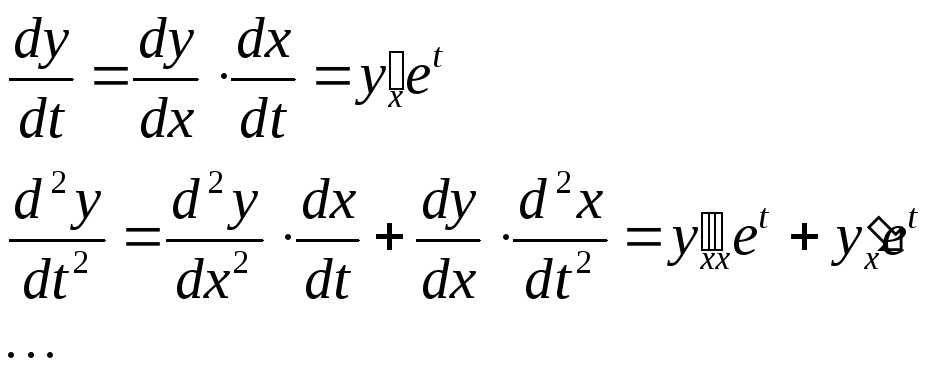
Можно
искать решения в виде y=xk,
тогда они имеют вид:
![]()
Линейные неоднородные уравнения.
![]() (1)
(1)
Если a0(x)0, то разделив на этот коэффициент уравнение (1), получим:
![]() .
(2)
.
(2)
![]() .
.
Если
на [a,b]
bi
и f
непрерывны, то (2) имеет единственное
решение, удовлетворяющее соответствующим
начальным условиям
![]() .
Если в явном виде выразить старшие
производные из (2), то получим уравнение,
правая часть которого удовлетворяет
теореме о существовании и единственности.
Так как оператор L
линейный, значит, для (2) выполняется:
.
Если в явном виде выразить старшие
производные из (2), то получим уравнение,
правая часть которого удовлетворяет
теореме о существовании и единственности.
Так как оператор L
линейный, значит, для (2) выполняется:
1).
![]() - решение (2), если
- решение (2), если
![]() - решение неоднородного уравнения (2), а
- решение неоднородного уравнения (2), а
![]() -
решение соответствующего однородного
уравнения.
-
решение соответствующего однородного
уравнения.
2).
Если
![]() -
решения
-
решения
![]() ,
то
,
то
![]() решение
уравнения
решение
уравнения
![]() .
.
Свойство
2 – принцип суперпозиции, он справедлив
при
![]() ,
если ряд
,
если ряд
![]() - сходится и допускает m-кратное
почленное дифференцирование.
- сходится и допускает m-кратное
почленное дифференцирование.
3)
Пусть дано операторное уравнение
![]() ,
где L
– это оператор с коэффициентами
,
где L
– это оператор с коэффициентами
![]() ,
все
,
все
![]() - вещественные. Функции U
и V
тоже вещественные. Тогда, если это
уравнение имеет решение
- вещественные. Функции U
и V
тоже вещественные. Тогда, если это
уравнение имеет решение
![]() ,
то решением этого же уравнения будут и
мнимая и вещественная части y:
,
то решением этого же уравнения будут и
мнимая и вещественная части y:
![]() и
и
![]() .
При чем каждый из них соответствует
решению
.
При чем каждый из них соответствует
решению
![]() .
.
Теорема.
Общее решение неоднородного уравнения
n-порядка
![]() на
отрезке [a,b]
при условии, что все коэффициенты
на
отрезке [a,b]
при условии, что все коэффициенты
![]() и
правая часть
и
правая часть
![]() -
непрерывные функции, можно представить
в виде суммы общего решения, соответствующей
однородной системы
-
непрерывные функции, можно представить
в виде суммы общего решения, соответствующей
однородной системы
![]() и
частного решения неоднородной -
и
частного решения неоднородной -
![]() .
.
Т.е.
решение
![]() .
.
Если невозможно в явном виде подобрать частные решения неоднородной системы, то можно воспользоваться методом вариации постоянной. Решение будем искать в виде:
![]() (3)
(3)
где
![]() решения
однородной системы,
решения
однородной системы,
![]() -
неизвестные функции.
-
неизвестные функции.
Всего
неизвестных функций
![]() -
n.
Они должны удовлетворять исходному
уравнению (2).
-
n.
Они должны удовлетворять исходному
уравнению (2).
Подставив
в уравнение (2) выражение y(x),
мы получим условия для определения
только одной неизвестной функции. Чтобы
определить остальные (n-1)-ну
функции, необходимо еще (n-1)-но
дополнительное условие, их можно выбрать
произвольно. Выберем их так, чтобы
решение (2) - y(x)
имело вид такой же, как если бы
![]() были
константами.
были
константами.
![]() ,
,
т.к.
![]() ведут себя как константы, то
ведут себя как константы, то
![]() ,
значит, и
,
значит, и
![]() .
.
![]()
…
![]()
Т.о.
мы получим (n-1)-но
условие дополнительно к уравнению (1).
Если подставить выражение для производных
в уравнение (1) и учесть все полученные
условия и то, что yi
– решение соответствующей однородной
системы, то мы получим последнее условие
для
![]() .
.
Перейдем к системе:
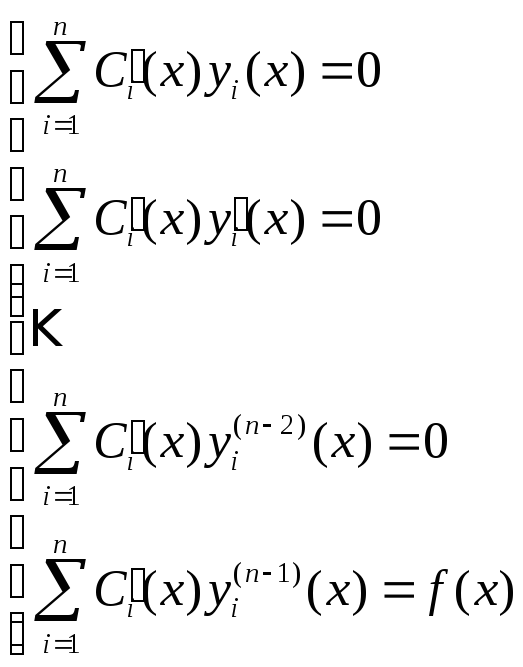 (3)
(3)
Определитель системы (3) – это (W) определитель Вронского, а т.к. yi – это решения однородной системы, то W0 на [a,b].
![]() (4)
(4)
Пример. Неоднородное уравнение
![]() ,
соответствующее ему однородное уравнение
,
соответствующее ему однородное уравнение
![]()
Решение ищем в виде y=ekx. Характеристическое уравнение k2+1=0, т.е. k1,2=i
y=eix=cos
x
+i
sin
x,
общее решение -
![]()
Воспользуемся методом вариации постоянной:
![]()
Условия
для
![]() :
:
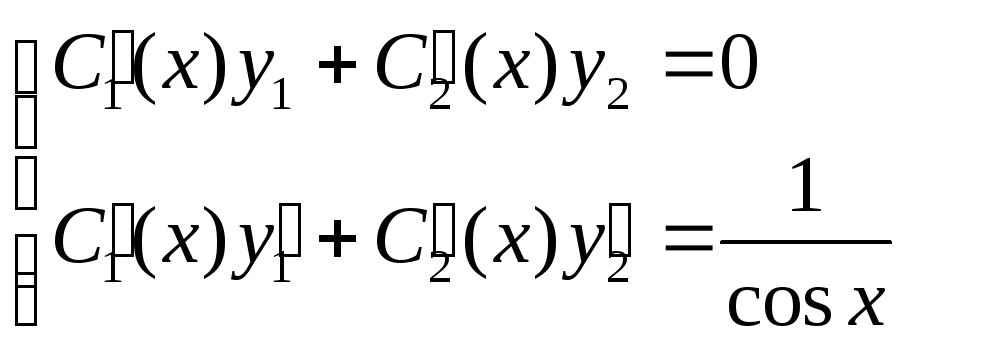 ,
что эквивалентно записи:
,
что эквивалентно записи:
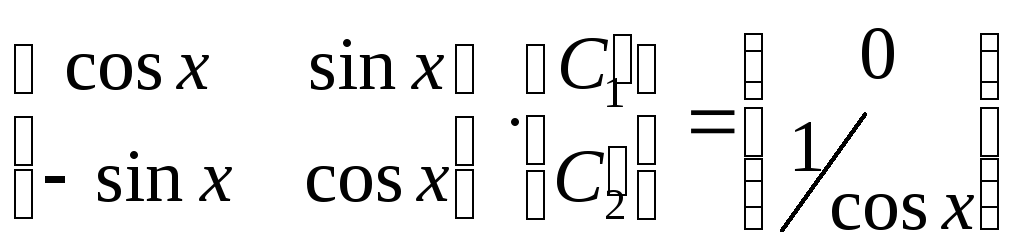
Отсюда: