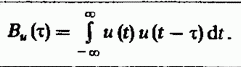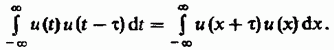46. Корреляционная функция. Корреляционный анализ случайных сигналов.
Автокорреляционная функция сигнала.
Для количественного
определения степени отличия сигнала
u(t) и
его смещенной во времени копии u(t-r) принято
вводить автокорреляционную функцию
(АКФ) сигнала u(t),
равную скалярному произведению сигнала
и копии:
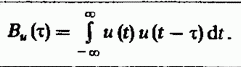
В дальнейшем будем предполагать, что
исследуемый сигнал имеет локализованный
во времени импульсный характер, так что
интеграл вида (3.15) заведомо существует.
Непосредственно видно, что
при r=0 автокорреляционная
функция становится равной энергии
сигнала:
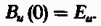
К числу простейших свойств АКФ можно
отнести ее четность:
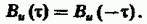
Действительно, если в
интеграле (3.15) сделать замену
переменных x=t-r, то
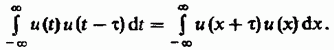
Наконец, важное свойство
автокорреляционной функции состоит в
следующем: при любом значении временного
сдвига r
модуль АКФ не превосходит энергии
сигнала:
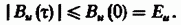
Этот факт непосредственно вытекает из
неравенства Коши — Буняковского (см.
гл. 1):
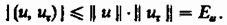
Итак, АКФ представляется
симметричной кривой с центральным
максимумом, который всегда положителен.
При этом в зависимости от вида
сигнала u(t) автокорреляционная
функция может иметь как монотонно
убывающий, так и колеблющийся характер.