!Оптика и квантовая механика / Задачи / 11 / zan01_02

Занятия 1,2

№5.73

В опыте Ллойда световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с волной, отраженной от зеркала З. В результате на экране Э образуется система интерференционных полос. Расстояние от источника до экрана . При некотором положении источника ширина интерференционной полосы на экране , а после того как источник отодвинули от плоскости зеркала на , ширина полос уменьшилась в раза. Найти длину волны света.

Р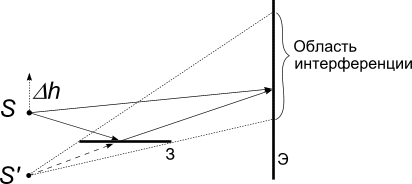ешение:

Систему из одного источника света и зеркала в опыте Ллойда можно заменить двумя когерентными источниками света (второй источник располагается на таком же расстоянии от зеркала, что и первый, но по другую сторону). Тем самым мы рассматриваем интерференционную картину от двух когерентных источников света.

Тогда мы знаем, что ширина интерференционной полосы в таком случае вычисляется по формуле: .

В нашей задаче запишем это выражение для двух случаев: до перемещения источника и после:

и ,

где - первоначальное расстояние от источника до зеркала. В условии сказано, что

.

Тогда

. ■

№5.74

Две когерентные плоские световые волны, угол между направлениями распространения которых , падают почти нормально на экран. Амплитуды волн одинаковы. Показать, что расстояние между соседними максимумами на экране , где -длина волны.

Решение:

Рассмотрим две плоские когерентные волны задаваемые уравнениями:

и

Здесь уже учтено, что амплитуды волны одинаковы и они когерентны. Тогда проведем рассуждения аналогичные тем, что были на лекции. Нам необходимо найти амплитуду результирующей волны, для этого воспользуемся методом векторных диаграмм (см. рисунок) и получим , где

Поскольку нас интересует расстояние между соседними максимумами, то

.

И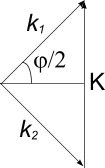з рисунка видно, что . Учитывая малость угла, получаем:

.

Как известно,

,

тогда

. ■

№5.75

На рисунке показана интерференционная схема с бизеркалами Френеля. Угол между зеркалами , Расстояния от линии пересечения зеркал до узкой щели S и экрана Э равны соответственно и . Длина волны света . Определить:

а) ширину интерференционной полосы на экране и число возможных максимумов;

б) сдвиг интерференционной картины на экране при смещении щели на по дуге радиуса с центром в точке О;

в) при какой ширине щели интерференционные полосы на экране будут наблюдаться еще достаточно четко?

Решение:

а) Найдем . Из треугольников и (у них угол - общий и есть по одному прямому углу) получаем, что . - внутренний, - центральный, тогда

.

Тогда по известной формуле ширина интерференционной полосы:

.

Количество возможных максимумов найдем, поделив ширину интерференционной картины на ширину одного максимума:

. ■

б) При повороте отношение смещений будет равно

. ■

в) Условие четкости картины для двух точечных источников света:

А у нас источник протяженный, поэтому

,

значит картина будет еще достаточно четкой при

. ■

№5.78

Р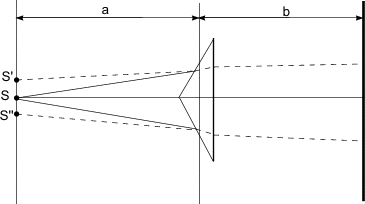асстояние от бипризмы Френеля до узкой щели и экрана соответственно и . Бипризма стеклянная с преломляющим углом . Найти длину волны света, если ширина интерференционной полосы на экране .

Решение:

При интерференционной картине от двух когерентных источников ширина полосы

,

где . Покажем, что

Из нижнего рисунка видно, что

,

также и (так как углы малые и мы можем избавиться от синусов), тогда

.

Итак получаем:

. ■

№5.80

Плоская монохроматическая световая волна падает нормально на диафрагму с двумя узкими щелями, отстоящими друг от друга на . На экране, расположенном за диафрагмой на , образуется система интерференционных полос. На какое расстояние и в какую сторону сместятся эти полосы, если одну из щелей перекрыть стеклянной пластинкой толщины ?

Р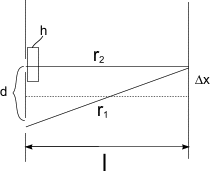ешение:

Будем следить за смещением центрального максимума. Разность хода двух лучей после появления пластинки:

,

где для второго луча разность хода складывается из хода внутри пластинки и хода вне пластинки. Тогда из этого выражения получаем:

.

Теперь из соответствующих треугольников получим:

и

Вычтя из первого уравнения второе, получим:

Или . ■

№5.81

На рисунке показана схема интерферометра для измерения показателей преломления прозрачных веществ. Здесь S – узкая щель, освещаемая монохроматическим светом , 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых , Д – диафрагма с двумя щелями. Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на полос. Показатель преломления воздуха . Определить показатель преломления аммиака.

Р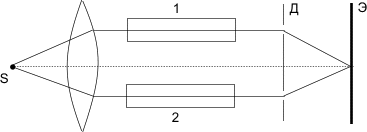ешение:

Очевидно, что интерференционная картина сместилась на максимумов:

Оптическая разность хода лучей в трубках:

. ■