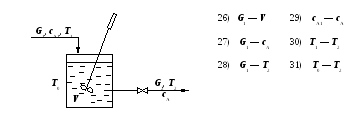МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНЖЕНЕРНОЙ ЭКОЛОГИИ

Кафедра технической кибернетики и автоматики

В. А. Миронова, Ю. Н. Софиева

Рабочая тетрадь

По теории автоматического управления

Нелинейные системы

Введение

Опыт преподавания теории автоматического управления показал, что приобрести достаточно устойчивые навыки в решении задач, возникающих при исследовании систем автоматического регулирования, можно только путем решения достаточно большого числа задач каждого типа. Исходя из этого в данной работе приводятся примеры типовых задач, методика их решения. Для каждого типа задач дано задание, включающее около 30 примеров.

Основные теоретические положения, необходимые для решения задач, а также методику их решения можно найти в конспекте лекций [1], сборнике задач и контрольных вопросов[2], а также учебниках[3, 4]. Приведенные примеры решения задач предназначены не для изучения методики их решения (они изложены слишком кратко и не освещают всех вопросов, возникающих при их решении), а для пояснения того, в какой последовательности и объеме должно быть дано их решение.

Приведенные задания должны быть выполнены при подготовке к семинарским занятиям и рубежному контролю в объеме, указанном преподавателем.

Тема 1. Получение передаточной функции объекта по заданному каналу

Пример 1.Найти передаточную функцию теплообменника, приведенного на рис. 1, по каналу- расходы,- температуры потоков,- объемы.

Выделяем выходные координаты, определяющие состояние объекта. В данном случае это температуры иПодробная структурная схема объекта приведена на рис. 2. Записываем уравнения математической модели, определяющие изменение выделенных выходных координат. При этом предполагаем, что жидкости, как в емкости, так и в рубашке, находятся в режиме идеального смешения, а теплофизические параметры: плотность, теплоемкость, коэффициенты теплопередачи - можно считать постоянными. Принимаем также, что все входные координаты, кромене изменяются во времени и принимают стационарные значения

Математическая модель включает уравнения тепловых балансов для жидкостей в емкости и рубашке:

Здесь - теплоемкости, а- плотности жидкостей в емкости и рубашке;- коэффициенты теплопередачи через стенку, разделяющую жидкости в емкости и рубашке, и наружную стенку,- соответствующие поверхности теплообмена.

Проверяем, являются ли полученные уравнения модели линейными относительно заданных входной и выходных координат. В данном случае первое уравнение нелинейно, поскольку второй член представляет собой произведение

Линеаризуем это уравнение, раскладывая правую часть его в ряд Тейлора в окрестности значенийсоответствующих статическому режиму, и оставляя только линейные члены:

где .

Получаем линеаризованное уравнение

Переходим к уравнению в отклонениях, вычитая из полученного линеаризованного исходное уравнение, записанное для статического режима

Получаем линеаризованное уравнение в отклонениях

Второе уравнение модели линейно относительно переменных поэтому сразу переходим к уравнению в отклонениях, вычитая из исходного уравнение для статического режимаПолучаем

где

.

Преобразуем полученные уравнения (3), (4) по Лапласу, обозначив изображения переменных

Получим

Выразим из второго уравнения (6) :

Подставив это выражение в первое уравнение, получим искомую передаточную функцию

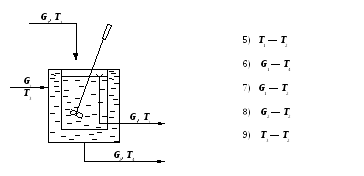
Задание 1.Получить передаточные функции для указанных объектов по заданным каналам. Обозначения переменных:

T - температура,

G - расход,

c - концентрация;

а) смеситель

(смешивают два раствора одного вещества А с разной концентрацией иобъем раствора в смесителе)

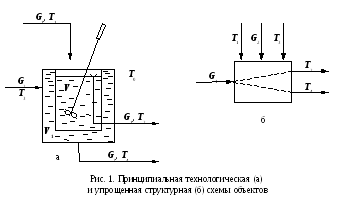
б) теплообменник

(обмениваются теплом два потока - один проходит через емкость, другой через рубашку. Объемы жидкостей )

в) химический реактор

(смешиваются два раствора, содержащие вещества AиB, происходит химическая реакция)

г) смеситель

(смешиваются два раствора, содержащие вещества AиB, невступающие в реакцию, смесь откачивается насосом,теплотой смешения пренебречь)

д) смеситель

(раствор жидкости, содержащий вещество A, проходит через емкость, где охлаждается,)