Домашнее задание № 1. «Химическая кинетика» Элементы теории

Химические реакции, протекающие в одну стадию, называются простыми. Такие реакции различают по молекулярности

Молекулярность реакции определяется числом частиц, принимающих участие в элементарном акте химического взаимодействия.

Молекулярность может быть равна 1, 2 или 3, соответственно, различают моно- би- и тримолекулярные реакции. Для простых реакций молекулярность совпадает с порядком реакции, а порядки по компонентам совпадают с наименьшими целочисленными стехиометрическими коэффициентами в левой части химического уравнения. Фактически, если известна молекулярность реакции, то понятен и ее истинный механизм, для установления которого проводят серьезные исследования.

Рассмотрим кинетику простых реакций 1, 2 и 3-го порядков.

Реакции первого порядка: A  L+ M

Порядок реакции (n) равен 1. Пусть концентрация вещества А (С_А) равна С, тогда скорость реакции (w=-dС/dt) в соответствии с законом действующих масс равна

-dС/dt = kС.

Латинская буква d здесь и далее обозначает знак дифференциала, то есть бесконечно малого изменения величины. Разделим переменные: -dС/С=kdt, проинтегрируем:-lnС = kt + const, определим константу интегрирования, учитывая, что в начальный момент времени: t = 0, С = С₀, отсюда const = -lnС₀. В итоге получаем: lnС – lnС₀ =- kt,

ln(С/С₀) = - kt, С = С₀ e^-kt . (1.1, 1.2)

Уравнения (1.1) и (1.2) называются кинетическими уравнениями реакции первого порядка в логарифмической (1.1) и экспоненциальной (1.2) форме.

Важной кинетической характеристикой процесса является время полупревращения (_1/2), то есть время, в течение которого прореагировала половина взятого вещества.

Определим эту величину для реакции первого порядка: С = 1/2С₀, ln(С₀/С) = ln2/k_1/2,

_1/2 = ln2/k = 0,69/k. (1.3)

Время полупревращения в этом случае не зависит от начальной концентрации исходного вещества.

Размерность константы скорости для реакций первого порядка: [k] = [с]^-1.

Реакции второго порядка: А + В  L.

Порядок реакции равен 2. Пусть С_A = С_B = С. Тогда -dС/dt = kС², -dС/С² = kdt. После интегрирования и с учетом начальных условий (t = 0, С = С₀) получаем:

1/С – 1/С₀= kt. (1.4)

Время полупревращения для реакций второго порядка обратно пропорционально начальной концентрации:

_1/2 = 1/(kС₀). (1.5)

Размерность константы скорости: [k] = [л/(моль с)].

Реакции третьего порядка: А + В + D L.

Величина n равна 3. Пусть С_A = С_B = С_D = С, тогда -dС/dt = kС³, -dС/С³ = kdt. После интегрирования, учитывая начальные условия (t = 0, С = С₀), получаем:

1/С² – 1/С₀²= 2kt. (1.6)

Время полупревращения для реакций третьего порядка обратно пропорционально квадрату начальной концентрации:

_1/2 = 3/(2kС₀²). (1.7)

Размерность константы скорости: [k] = [л²/(моль² с)].

В представленных кинетических уравнениях под символом «С» понимают текущую, то есть наблюдаемую в данный момент времени молярную концентрацию соответствующих исходных веществ (С = C_т.). Существует также понятие прореагировавшей концентрации (C_пр), характеризующее ту часть концентрации данного исходного вещества, которая превратилась в конечный продукт. Прореагировавшая концентрация связана с текущей и исходной (C₀) соотношением:

С₀ = C_т + C_пр (1.8).

В расчетах по уравнениям (1.1-1.7) нужно знать величину константы скорости реакции (k). Эту характеристику можно найти с помощью уравнения Аррениуса, если известны предэкспоненциальный множитель (k₀), энергия активации (Е) и температура (Т):

k = k₀e^-E/RT (1.9)

Значение константы скорости можно также определить графическим способом. Так, уравнения (1.1), (1.4) и (1.6) представляют собой прямолинейную зависимость соответствующих функций концентраций от времени: при n = 1 линейно от времени зависит lnC, при n = 2 – 1/С, при n = 3 – 1/С² (рис. 1, 2, 3). На этой закономерности основан графический метод определения порядка реакции, позволяющий также определить и значение k.

Пусть n = 1 или 2. Тангенс угла наклона (α) соответствующей прямой к оси Х (ось времени) равен константе скорости (рис 1.1, 1.2) - tgα = k. При n = 3 удвоенная константа скорости равна тангенсу угла (α) наклона прямой (рис. 1.3) - 2 tgα = k. Не представляет затруднений нахождение времени полупревращения из этих графиков.

ln(C₀/2)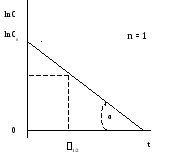

Рис. 1.1

_1/2

_½

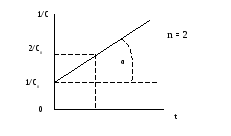
Рис. 1.2

t

Рис. 1.3

В присутствии катализатора скорость химической реакции возрастает, что связано с изменением механизма реакции, приводящего к снижению энергии активации процесса. При катализе катализатор и реагирующее вещество образуют промежуточное соединение, которое в результате дальнейших преобразований превращается в конечный продукт, высвобождая катализатор. Энергетические затраты таких процессов ниже, чем в отсутствии катализатора. Каталитические реакции являются сложными, так как протекают в несколько стадий. Скорость процесса определяется скоростью самой медленной стадии катализа.

Величиной, определяющей ускорение реакции в при катализе, является соотношение констант скоростей реакций в присутствии (k_к) и отсутствии (k) катализатора: k_к/ k_. Это значение можно рассчитать, если известна величина снижения энергии активации ∆Е. В расчетах будем полагать, что рассматриваемая реакция является односторонней, то есть необратимо протекает слева направо в соответствии с уравнением реакции.

Пусть Е^К = (Е - Е) – энергия активации прямой реакции в присутствии катализатора, Е – то же, но без катализатора. Тогда константа скорости прямой реакции в присутствии катализатора - k^K = k₀ exp[-(E - E)/RT], без катализатора - k₁ = k₀ exp(-E/RT).

Ускорение при катализе равно:

k^K/ k = exp (E)/RT). (1.10)