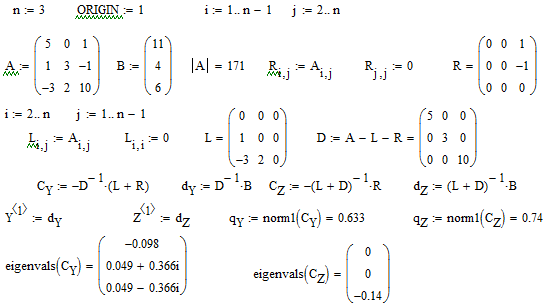ВМ 2 СЛАУ

2. Методы решения систем линейных алгебраических уравнений.

Все методы решения систем линейных алгебраических уравнений (СЛАУ) можно разбить на прямые и итерационные методы.

К прямым методам относят те, которые должны привести к решению за конечное число арифметических операций. Часто прямые методы называют точными, поскольку погрешности в них могут появиться только за счет округлений. Мы уже познакомились с двумя прямыми методами – с методом Крамера и с матричным методом. Они весьма привлекательны в теоретическом плане, но крайне неэффективны в вычислительном отношении (вспомните о проклятии размерности!). Обратимся к широко распространенному способу решения СЛАУ, известному как метод Гаусса, суть которого - последовательное исключение неизвестных

Рассмотрим произвольную систему линейных алгебраических уравнений с не известными:

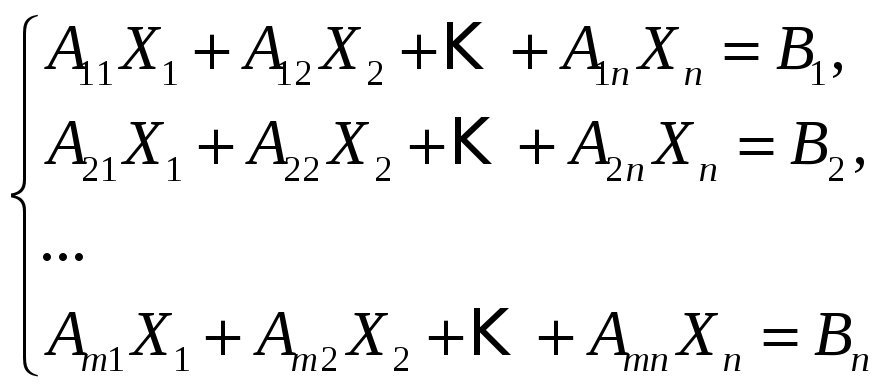(2.1)

Здесь - матрица коэффициентов системы; - матрица неизвестных; - матрица свободных членов. При решении системы удобно проводить выкладки в сокращенной записи – над расширенной матрицей

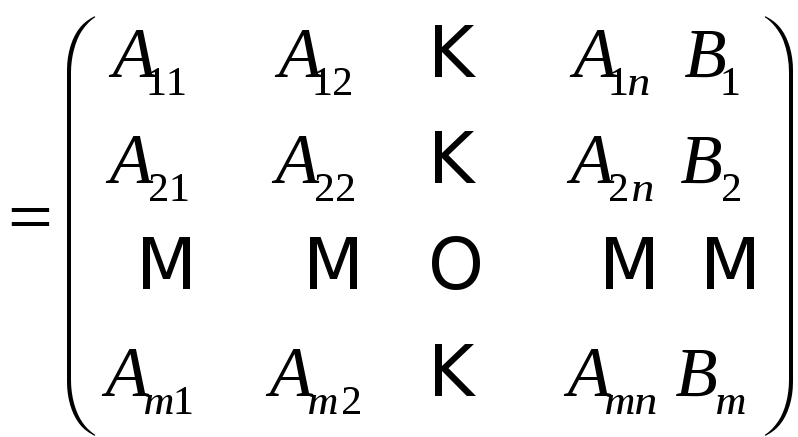(2.2)

Существование и единственность решения СЛАУ определяются соотношением трех величин – ранга матрицы системы , ранга расширенной матрицы и числа неизвестных .

По теореме Кронекера - Капелли необходимым и достаточным условием существования хотя бы одного решения системы (2.1) служит равенство рангов . В таком случае система называется совместной.

Если у совместной системы ранг совпадает с числом неизвестных , то она имеет единственное решение и система называется определенной.

Если же у совместной системы ранг меньше числа неизвестных , то у системы бесконечно много решений и система является неопределенной.

Вспомним, что в линейной алгебре минорами - ого порядка произвольной матрицы называются определители квадратных матрицы, составленных из элементов матрицы , стоящих на пересечениях произвольных строк и столбцов матрицы . Наибольший из порядков ненулевых миноров матрицы называют её рангом.

Однако к непосредственному вычислению рангов матриц относится все то, что мы говорили о методе Крамера и матричном методе. Парадоксально, но проще всего ранги матриц определять в процессе решения системы (2.1) методом Гаусса, который предполагает последовательное исключение неизвестных в результате элементарных преобразований, не влияющих на ранг. К таким преобразованиям относится перестановка строк или вычитание строк, одна из которых предварительно умножена на специально подобранное число.

Очевидно, что хотя бы один из коэффициентов при не равен нулю. Всегда можно принять, что , если необходимо, в системе уравнения можно поменять местами. Тогда первый шаг прямого хода по методу Гаусса будет состоять в замене исходной СЛАУ (2.1) на равносильную ей систему

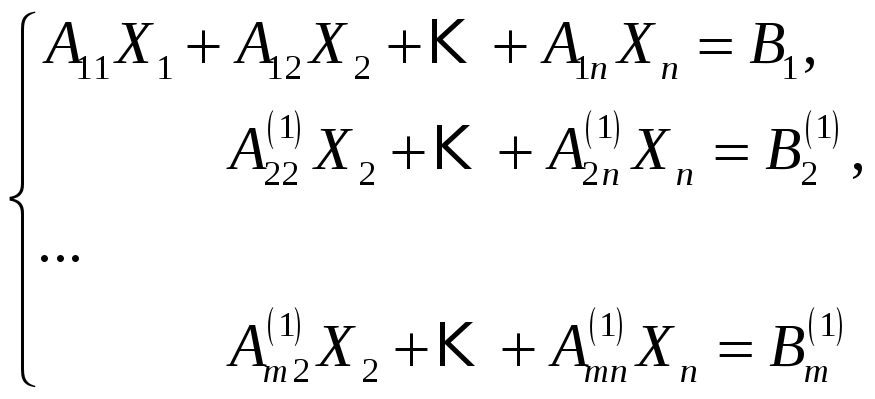. (2.3)

Здесь новые коэффициенты вычисляются по формулам

(2.4)

Преобразование сводится к вычитанию первой строки из остальных, в результате чего мы получаем новую усеченную систему, в которой число уравнений и число неизвестных уменьшились каждое хотя бы на единицу.

Второй и последующие шаги прямого хода повторяют предыдущий. В конце прямого хода мы получим систему

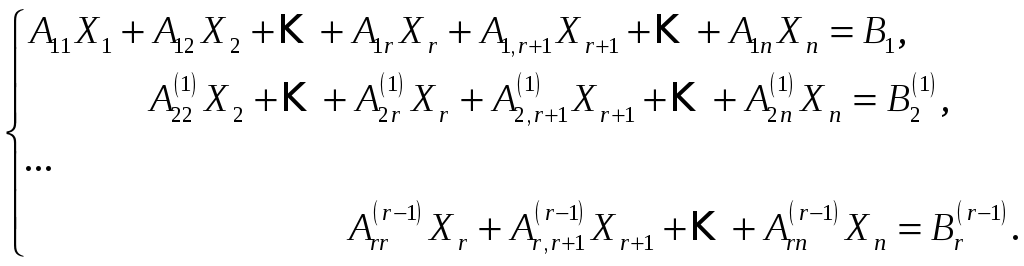(2.5)

В процессе исключения неизвестных могли появиться тождества 0=0, их следовало просто отбрасывать. Появление строк типа говорит о несовместности системы. Ранг матрицы определяется числом оставшихся уравнений . Прямой ход по Гауссу заканчивается. Если оказалось, что , то система является определенной. Её ненулевой определитель равен произведению коэффициентов, оказавшихся на главной диагонали (разумеется, с учетом того, что каждая возможная перестановка местами двух уравнений меняет знак определителя системы):

(2.6)

Далее осуществляется обратный ход по Гауссу. Последовательно, начиная с - го уравнения и заканчивая вторым, делят очередное уравнение на коэффициент и, умножая его на коэффициенты при , вычитанием добиваются исключения его из всех предыдущих уравнений.

В случае приходим к соотношениям, определяющим единственное решение системы (2.1):

. (2.7)

В случае точно также получаем формулы, задающие общее решение неопределенной системы

. (2.8)

Здесь неизвестные объявляются свободными, они могут принимать любые значения. Остальные – базисные неизвестные выражаются через свободные неизвестные по формулам (2.8).

Пример 2.1 Заданы квадратная матрица системы порядка и вектор-столбец свободных членов :

.

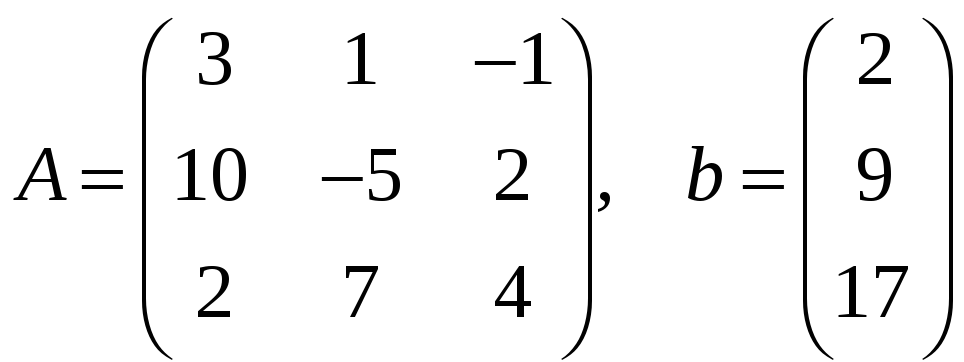Требуется

1. Ввести в компьютер массивы исходных данных и , установить 1 в качестве начала отсчета индексов массивов. Вычислив определитель, проверить невырожденность матрицы .

2. Составить расширенную матрицу 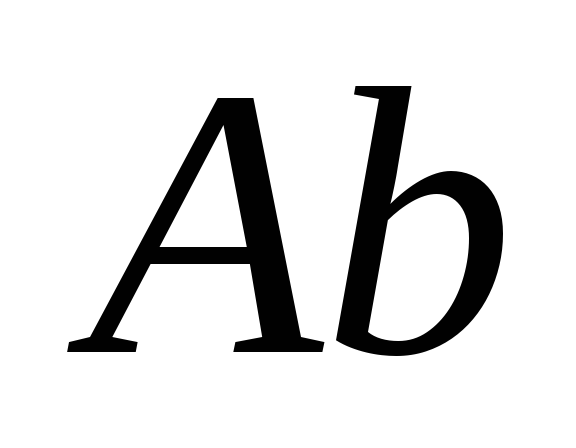, сравнив её ранг с рангом матрицы и с числом неизвестных, сделать вывод о совместности и определенности системы .

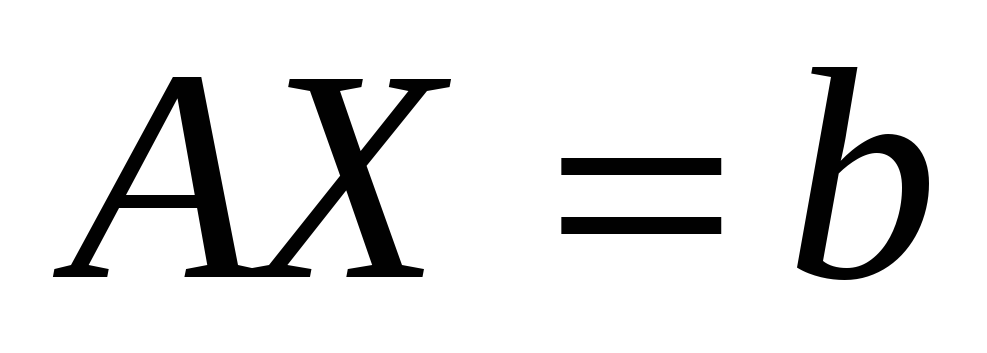3. С помощью элементарных преобразований над строками расширенной матрицы 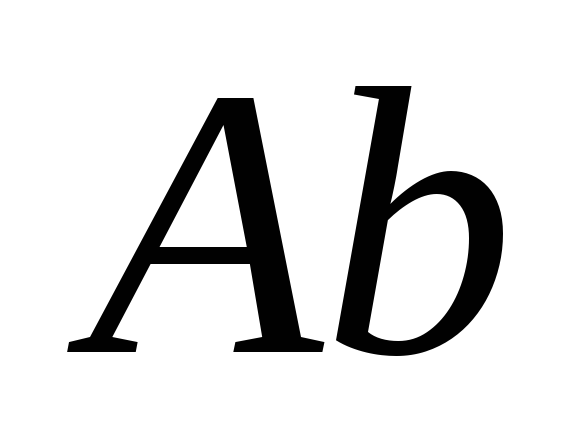провести последовательное исключение неизвестных по шагам прямого хода метода Гаусса.

4. Вычислить определитель системы по диагональным элементам расширенной матрицы в конце прямого хода.

5. Осуществив преобразования обратного хода, получить решение системы.

6. Сравнить полученные результаты с результатами применения встроенных функций.

Решение. Привычное для нас начало счета индексов элементов массивов с единицы устанавливается командой «ORIGIN:=1», по умолчанию индекс первого элемента массива равен нулю. Ранг матрицы M вычисляется функцией . Программа решения системы приведена на рис. 2.1 и 2.2.

Рис. 2.1

В начале каждого шага процесса Гаусса мы транспонируем расширенную матрицу и обозначаем её как . Вместо преобразования строк расширенной матрицы мы работаем с векторами-столбцами . Номера преобразуемых столбцов задаются ранжированной переменной: - на первом шаге, - на втором шаге и т.д. Формулы преобразований соответствуют формулам (2.4). В конце каждого шага транспонируется, чтобы можно было удостовериться, что очередной столбец ниже главной диагонали заполнился нулями. Сейчас мы можем очень экономичным образом вычислить определитель матрицы . Он равен произведению элементов, стоящих на главной диагонали в преобразованной расширенной матрице, если, разумеется, не было перестановок уравнений. Для вычисления определителя можно использовать кнопку в панели Calculus (Анализ). Затем, используя ранжированную переменную , делим каждую строку на её диагональный элемент. Прямой ход закончен, переходим к обратному ходу, осуществляемому аналогичным образом. Здесь нулями заполняется треугольник над главной диагональю, на каждом шаге обратного хода используются убывающие ранжированные переменные и т.д. Данное решение следует сравнить с решениями, полученными с использованием функций и .

Эти функции построены профессионалами на основе метода Гаусса. Наша программа, приведенная на рис. 2.1 и 2.2, носит учебный характер. В заключение порекомендуем для облегчения набора использовать операцию копирования на каждом шаге с внесением необходимых изменений.

Рис. 2.2

Перейдем к итерационным методам решения систем линейных алгебраических уравнений, ограничимся проблемой нахождения единственного решения определенной системы

(2.9)

Здесь - квадратная матрица коэффициентов системы; - матрица неизвестных; - матрица свободных членов. Ранг системы равен числу неизвестных .

Различные варианты метода простых итераций предполагают переход от системы (2.9) к эквивалентной системе

(2.10)

Задачу о поиске точного решения систем (2.9) или (2.10) трактовать как задачу о неподвижной точке линейного отображения в - мерном пространстве. Итерационный процесс, определяющий последовательность приближений к неподвижной точке , определяется очевидным рекуррентным соотношением

. (2.11)

Начальное приближение считается известным. Итерационный процесс (2.11) принято называть методом простых итераций.

Необходимым и достаточным условием сходимости процесса простых итераций к точному решению при любом начальном приближении является требование, чтобы все собственные значения матрицы по модулю были меньше 1. [вержбицкий]

Более простым достаточным условием сходимости служит требование

. (2.12)

Из (2.17) следуют полезные оценки погрешности приближений: апостериорная оценка

, (2.13)

которую используют для остановки процесса при достижении заданной точности, и более грубая априорная оценка:

, (2.13)

по которой до проведения расчетов можно найти число итераций, необходимое для достижения заданной точности. Отметим, что в данных оценках предполагается использование согласованных матричных и векторных норм.

Различные варианты метода простой итерации различаются способом перехода между системами (2.9) и (2.10). Рассмотрим метод, предложенный немецким математиком Карлом Якоби (1804-1851). Представим матрицу исходной системы (2.9) в виде суммы матриц: диагональной матрицы и двух строго треугольных с нулевой диагональю и (левой и правой). Тогда система (2.9) запишется в виде

(2.14)

и если на главной диагонали исходной матрицы не было нулей, то у существует обратная матрица - диагональная матрица с диагональными элементами . Тогда мы можем преобразовать (2.9) в систему (2.10), где

. (2.15)

Метод итераций Якоби в матричном виде определяется рекуррентной формулой (2.11) с матрицами (2.15). Отметим, что в матрице на главной диагонали стоят нули. Выпишем рекуррентную формулу Якоби в развернутом виде:

(2.16)

Доказано простое достаточное условие сходимости последовательности итераций Якоби (2.16), которое называют диагональным преобладанием:

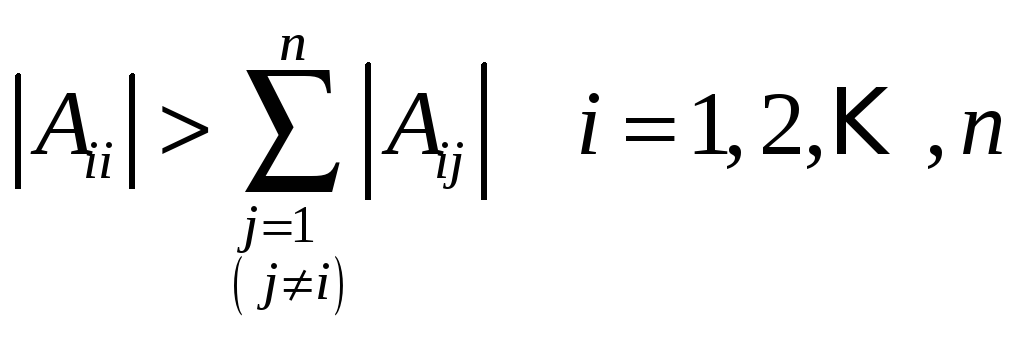(2.17)

Другой немецкий ученый – астроном и математик Людвиг Зейдель (1821-1896) предложил, как усовершенствовать метод Якоби и ускорить сходимость. Для этого на каждом шаге итераций нужно уже найденную из первого соотношения (2.16) компоненту следующего приближения подставить в правую часть второго соотношения. Затем уже найденные компоненты и следующего приближения подставить в правую часть третьего соотношения и т.д. В итоге получаем рекуррентные формулы известные как формулы Зейделя:

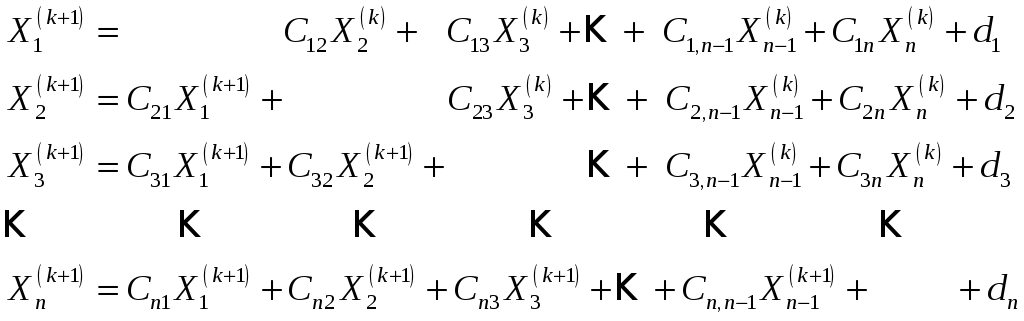(2.18)

Сравним метод Якоби:

(2.19)

и Зейделя:

. (2.20)

в неявной матричной форме. Сопоставление (2.19) и (2.20) показывает, что оба метода сводятся к методу простой итерации (2.11), только матричные коэффициенты вычисляются по разным формулам. Для того, чтобы не было путаницы выпишем рекуррентную формулу Якоби еще раз:

. (2.21)

Здесь коэффициенты определяются формулой (2.15), следующей из (2.19)

. (2.22)

И, наконец, запишем рекуррентную формулу Зейделя:

. (2.23)

Здесь коэффициенты определяются формулой, следующей из (2.20):

. (2.24)

Доказано, что условие диагонального преобладания (2.17) является достаточным условием сходимости не только для метода Якоби, но и для метода Зейделя, причем для метода Зейделя оно обеспечивает более быструю сходимость [ Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. - М.: Высшая школа, 2000.].

Отметим еще один важный класс систем (2.9) с симметричной положительно определенной матрицей (так называемые нормальные системы), для которых метод Зейделя сходится. [ Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970.] Там же доказано, что если любая невырожденная матрица при умножении слева на транспонированную матрицу становится симметричной положительно определенной, а значит система (2.9) переходит в нормальную систему

. (2.25)

Такое преобразование системы называют симметризацией Гаусса [ Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. - М.: Высшая школа, 2000.]

Пример 2.2 Заданы квадратная матрица системы порядка и вектор-столбец свободных членов :

.

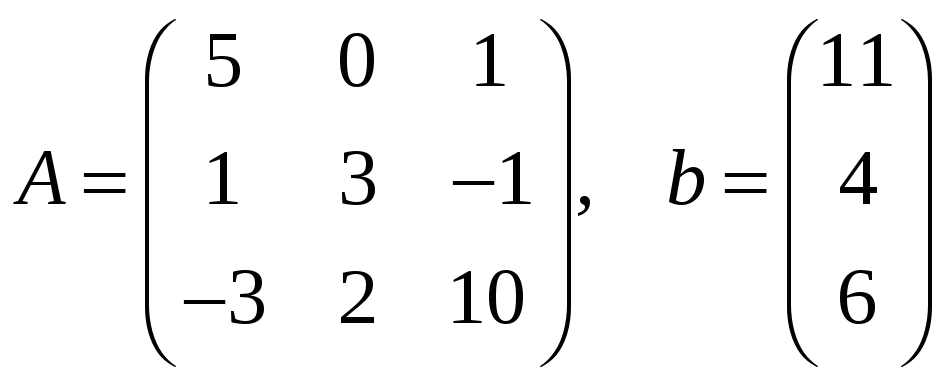Требуется

1. Ввести в компьютер массивы исходных данных и , установить 1 в качестве начала отсчета индексов массивов. Вычислив определитель, проверить невырожденность матрицы .

2. Представить матрицу в виде суммы матриц: диагональной матрицы и двух строго треугольных с нулевой диагональю и 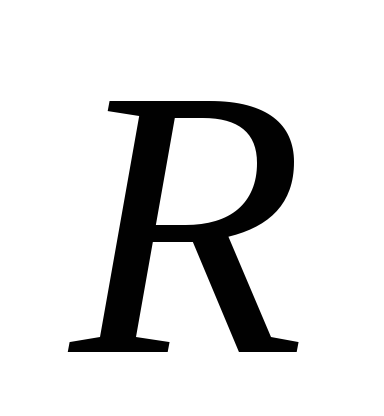(левой и правой). Вычислить коэффициенты рекуррентных формул Якоби (2.21) и Зейделя (2.23) по формулам (2.22) и (2.24).

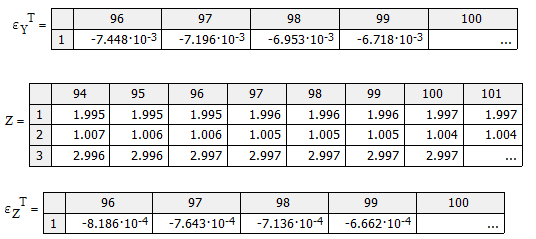
3. Вычислить 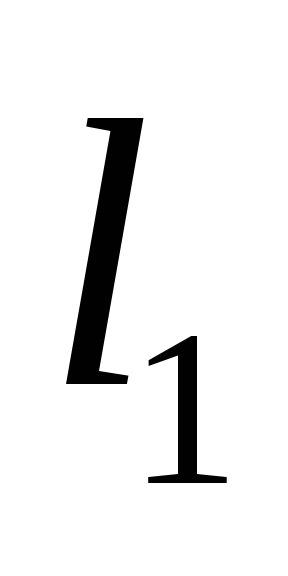- нормы и собственные значения матриц и , используя функции и 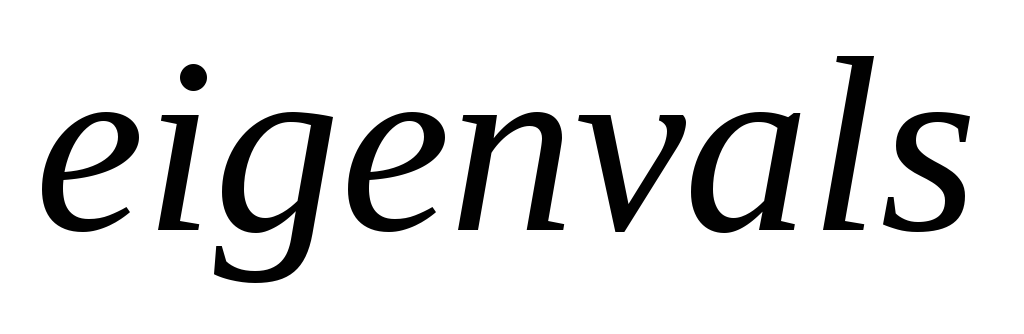. Сделать выводы о сходимости процессов итераций по методам Якоби и Зейделя.

4. Принять 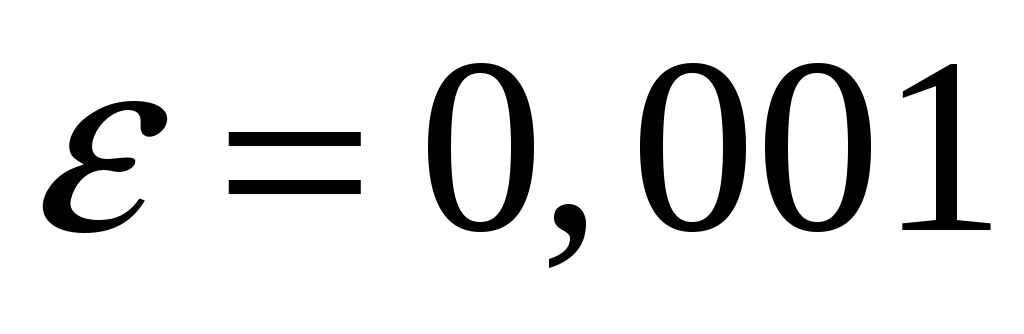за точность решения системы 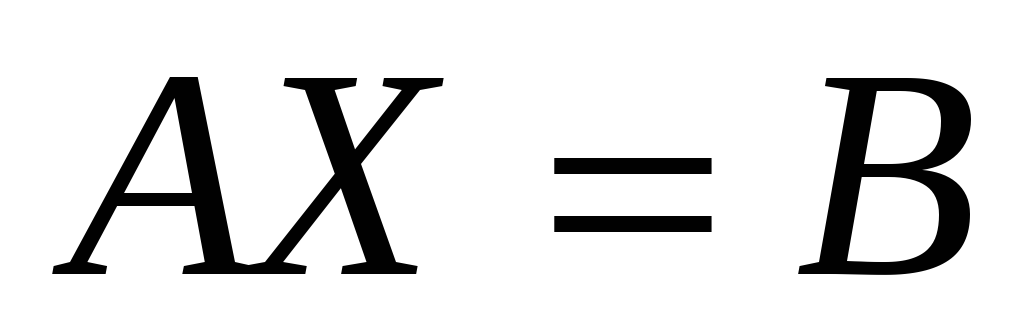по 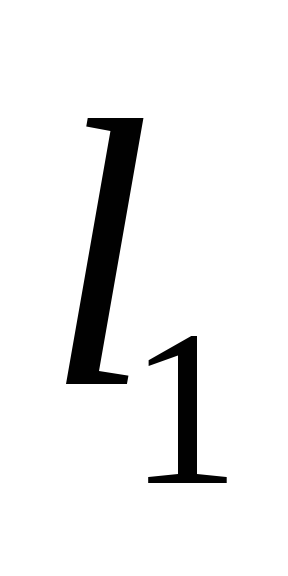- норме. Оценить необходимое количество итераций по формуле (2.13) и рассчитать их, контролируя достигнутую точность по формуле (2.12).

5. Осуществить симметризацию Гаусса и убедиться в сходимости итераций по методу Зейделя.

Решение. Начальные приближения могут быть выбраны произвольно. Для определенности примем за начальные приближения векторы свободных членов и . Программа решения системы приведена на рис. 2.3 - 2.5.

Рис. 2.3

На рис. 2.3 рассмотрен пример система с диагональным преобладанием. Кроме того нормы матриц и , а также собственные значения по модулю меньше 1. Это говорит в пользу сходимости итераций. Расчет подтверждает наши выводы.

На рис. 2.4 приведен пример системы, для которой итерационные процессы должны расходятся (почему?), и подтверждение сделанного предположения.

Рис. 2.4

И, наконец, на рисунке (2.5) приведены результаты применения упомянутой симметризации Гаусса к системе, которую не удалось решить итерационными методами.

Рис. 2.5