Шпоры по предм Физика Хим Полупроводников (Шерченков ЭТМ 3) / Шпоры по предм Физика Хим Полупроводников (Шерченков ЭТМ 3) / Шпоры по отдельности / 10

10. Функция распределения ферми Дирака и ее свойства.

Число е в интервале энергий dE: dn=N(E)*f(E)dE, где N(E)- плотность состояний. f(E)- функция распределения (вероятность заполнения) Функция распределения определяется функцией Ф-Д. 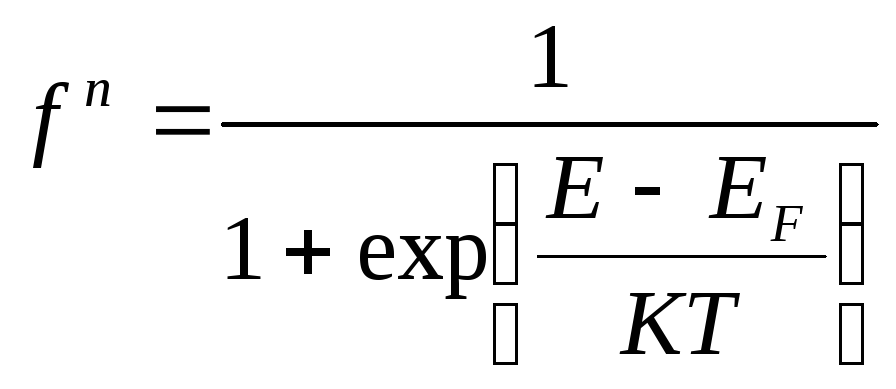(1);

Вероятность что состояние с энергией Е свободно. 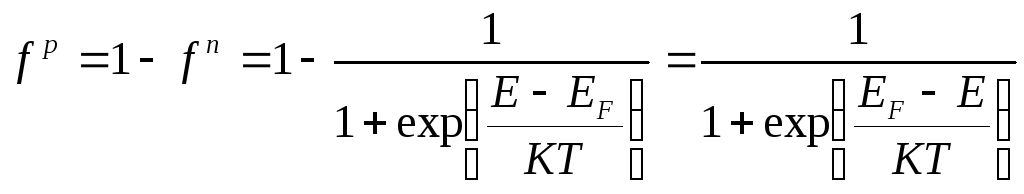(2)

Рассмотрим свойства функции Ф-Д. Продиф. Ее по энергии.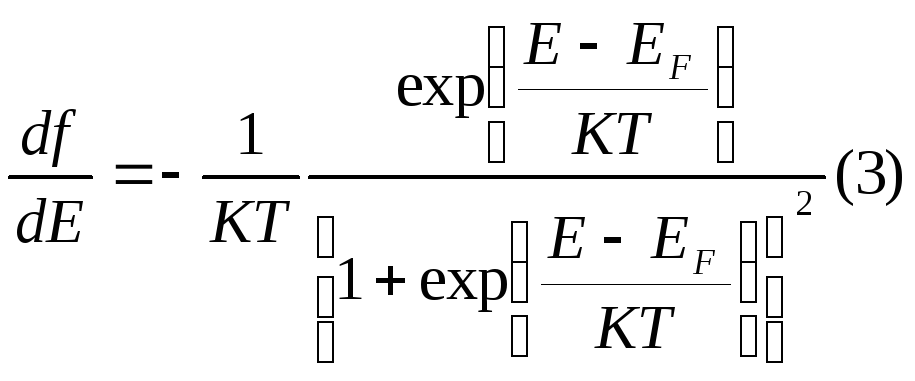 умножим числ, и знам. на , получим

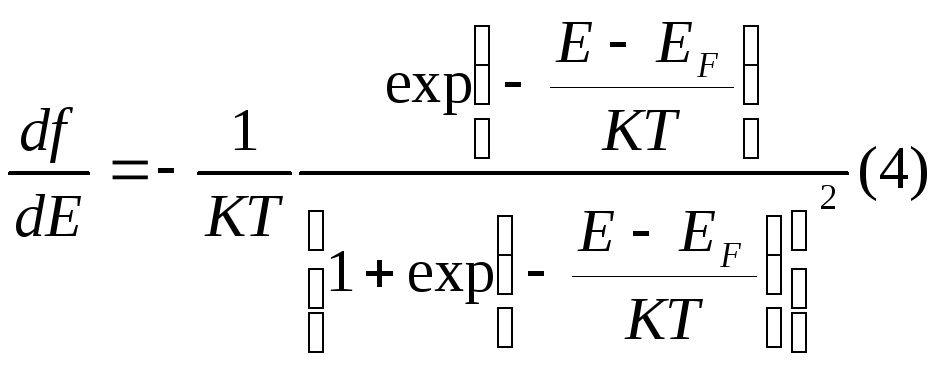
В результате имеем что ф-я четная симметричная относительно точки .

Т.е. Она будет иметь вид ∆-функции.

Очевидно, что при Е=Е_F,

При Т→0 .

при T=0К f(E)=1, при Е<E_F

f(E)=0, при Е>E_F

при Т>0К Е=E_F, f(E)=0.5

Зависимость уровня ферми от температуры.

Приближенное интегрирование и решение дает следующую зависимость.

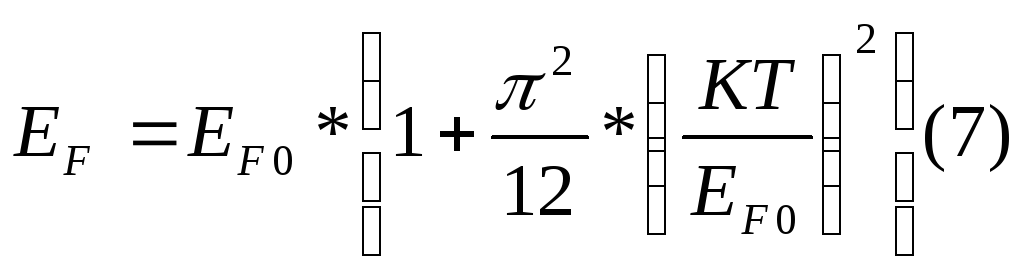
Изобразим функцию f(E).

Е_F уменьшается с ростом температуры за счет того, что тепловое возмущение позволяет заполнять уровни выше E_F0 и требует чтобы какое то число состояний ниже E_F0 оставалось незанятым. Поскольку N(E) растет с энергией, энергия соответствующая 50% заполнению должна снижаться по мере того как увеличивается тепловое уширение переходной области.

Если E-E_F>>KT, то ф-я Ф-Д

Итак чем выше температура, тем сильнее размывается ф-я Ф-Д, однако поскольку это размывание происходит в интервале энергий КТ, что при комнатной температуре составляет ничтожно малую величину, то энергия газоносителей практически не меняется. Эл Газ в котором энергия носителе не зависит от Т называется вырожденным. Определим n(E)=N(E)*f(E)=