Курсовые / Колебания и волны в плазме / колебания и волны1

II. Колебания и волны в плазме в отсутствие магнитного поля.

Общий подход к описанию периодических колебаний и волн. Уравнения, описывающие движение плазмы, допус­кают периодические решения — колебания. В зависимости от типа возбуждения (граничных и начальных условий) пе­риодически меняющимися величинами могут быть про­дольная или поперечная компоненты Е- и В-полей, значе­ния n_e, n_i и другие параметры, определяющие локальное состояние плазмы. При классификации волн в плазме по характеристикам осциллирующих Е-, В-полей различают электромагнитные (возбуждаются колебания как Е, так и В) и электростатические (заметно осциллирует лишь Е). По взаимному расположению волнового вектора k и внеш­него постоянного магнитного поля В₀ различают парал­лельные (k || В₀) и перпендикулярные волны (kВ₀). Если в волновом движении участвуют лишь электроны, то волны — электронные, а если и электроны, и ионы, — ионные. Различие природы и спектрально-энергетических характеристик позволяет проводить их отождествление в реальных плазменных объектах.

Любое периодическое движение с помощью фурье-разложения можно представить в виде суперпозиции синусоидальных гармонических колебаний с различными часто­тами и длинами волн (или волновыми числами k =).

При малой амплитуде колебаний * n (где — «фоновое» значение осциллирующей величины , = *+) различные гармоники фурье-разложения не вза­имодействуют друг с другом, и для описания колебаний достаточно проанализировать малые колебания гармониче­ской формы

(r,t) = +*exp[i(kr + wt)] ; (2.1),

здесь k — волновой вектор, w — круговая частота колеба­ний, i — мнимая единица.

Физический смысл здесь имеет действительная часть Re () (мнимую часть после получения конечного резуль­тата не учитывают). Если колебания имеют постоянную амплитуду, то Re() = +*cos (kr + wt); если они затухают, то полагают, что w — комплексная величина, w = Re (w) + i, >0 —декремент затухания колеба­ний, функция

Re ()=+*exp(-tc)cos(kr + Re (w)t) экспоненциально уменьшается. Если происходит раскачка колебаний, то < 0, где — инкремент неустой­чивости.

Точка постоянной фазы (например, узел = или гребень волны = + *) перемещается с фазовой ско­ростью, которая определяется из соотношения _ph = w / k

Если w /k > О, то волна движется в направлении на­растания пространственной координаты, если w /k < 0 — в обратном направлении. Обычно считается w 0, а знак (+ или —) (и направление) приписывается k. Фазовая скорость волны в плазме может превышать скорость света с. Это не противоречит теории относительности, т.к. бес­конечно длинный волновой пакет постоянной амплитуды не может переносить ин­формацию, скорость пере­дачи которой ограничена значением с. Информация содержится в нарушении периодичности, например в амплитудной модуля­ции, образованной сложением двух волн с близкими w и k (рис. 2.1), и передается с групповой скоростью _g =w = dw | dk, а _g с.

Рис. 2.1. Пространственное распределение электрического поля суммы двух волн с близкими частотами.

Фазовая скорость электромагнитной волны определяет показатель преломления среды: n = c / _ph.

При п 0, т.е. _ph, происходит отсечка элек­тромагнитной волны в плазме; при п, т.е. _ph 0, возникает резонанс. Если волна распространяется через плазменный объем с переменными локальными параме­трами (n_e, B₀ и др.), то могут быть выполнены условия отсечки или резонанса (при этом в точке отсечки волна, как правило, отражается, а в резонансе — поглощается).

Фазовая и групповая скорости, декременты затухания, границы устойчивости и характерные времена развития неустойчивостей и другие характеристики колебаний опи­сываются дисперсионным соотношением — зависимостью w = w (k). Для его получения решение в виде (2.1) при =const, *= const подставляется в систему уравне­ний, описывающую динамику плазмы в заданном диапазоне параметров и типе возмущений (например, систему магнит­ной гидродинамики, уравнение Власова и др.).

Взаимодействие волн с частицами и затухание Ландау.

При распространении в плазме электростатических волн на заряженные частицы действует периодическое по простран­ству и времени знакопеременное электрическое поле.

Если фазовая скорость гармонической волны _ph на­много меньше скорости заряженной частицы, то последняя (при отсутствии столкновений) совершает колебательные движения с малой постоянной амплитудой и с частотой волны w₀ , обмен энергией с волной в среднем за период равен нулю.

В плазме с ненулевой температурой, однако, существует достаточно широкое распределение частиц по скоростям; для частицы, скорость _i которой близка к фазовой ско­рости волны (резонансной частицы), поле меняется с ча­стотой w' n w (при _i = _ph — w' = 0) и время действия положительной (отрицательной) полуволны электрического поля на частицу достаточно велико, чтобы она успевала за­метно ускориться (замедлиться).

Поскольку время ускорения в полуволне Е-поля не равно в точности времени замедления (в противоположно направленной полуволне), вследствие конечного изменения скорости частиц при _j < _ph , в среднем по осцилляциям частиц j ускоряются, а при _j > _ph — замедляются.

Если среди частиц с _{j ph} преобладают относи­тельно более медленные частицы (_j < _ph), то затраты энергии на ускорение преобладают над высвобождением энергии за счет торможения (менее многочисленных) ча­стиц с _j >_ph при этом расходуется энергия колеба­ний — происходит бесстолкновительное поглощение волны (затухание Ландау) (заряженные частицы с _{j ph} дви­жутся таким образом, что амплитуда волны Е-поля умень­шается).

Таким образом, различные возмущения и волны могут затухать и в бесстолкновительной плазме, в которой отсут­ствует хаотизация направленных скоростей частиц вслед­ствие парных рассеяний. Достаточным условием затухания Ландау является монотонный спад функции распределения частиц по скоростям при _{j ph} .

Это условие, в частности, всегда выполняется при рав­новесной, максвелловской функции распределения частиц.

В противоположном случае, когда среди квазирезонанс­ных частиц быстрых (_j >_ph) больше, чем медленных (_j <_ph), преобладает замедление частиц, при этом их кинетическая энергия переходит в энергию волны — про­исходит нарастание амплитуды колебаний (квазирезонанс­ные заряженные частицы движутся так, что их сгущения и разрежения сфазированы с волной и увеличивают ее ам­плитуду). Для этого необходимо, чтобы функция распре­деления в окрестности _{j ph} нарастала с увеличением _j . В результате такого взаимодействия плазмы и волны неустойчивое распределение частиц в окрестности _ph эволюционирует к устойчивому — с = 0 («плато», волна распространяется без нарастания или затухания) или с < 0 (происходит затухание Ландау). Корректный анализ бесстолкновительного коллективного взаи­модействия с плазмой гармонических малых электронных электростатических (плазменных) колебаний, основанный на кинетическом уравнении Власова и уравнениях Макс­велла, приводит к декременту затухания Ландау вида

_L = = ; (2.2^*) ,

здесь f(v) — одномерное распределение частиц в напра­влении k. Например, в случае максвелловского распреде­ления,

= , (2.3^*)

декремент затухания Ландау равен

_L = . (2.4^*)

Из (2.4) видно, что при kr_D n 1 затухание Ландау мало, а при kr_D ~ 1 становится существенным.

Плазменные колебания и волны. Электрическое поле и локальный потенциал в плазме (даже при отсутствии внешнего возмущения) испытывают плазменные колеба­ния, иллюстрацией чего служит «плазменный конденса­тор» — тонкий (х < r_D) плоский слой ионов и электронов; при смещении электронов (на расстояние х) относительно ионов возникает возвращающее электростатическое поле Е = n_eex /₀ и под действием электростатических и инер­ционных сил m_e d²x/dt² = E возбуждаются колебания электронов около положения равновесия (ионы можно счи­тать покоящимися из-за того, что М_i . m_e).

Частота колебаний в «плазменном конденсаторе» равна плазменной частоте = [n_ee²/(m_e)]^1/2. Частота плазменных колебаний совпадает с , если плазма столкновительная либо если в бесстолкновительной плазме Т_e n Т'_e. = m_e(3k)= 0,_i = 0, и плазма является бес­конечно протяженной; в этом случае не зависит от k, = d/dk = 0, т.е. пространственно-локализованное воз­мущение этим типом колебаний не распространяется.

В плазме с Т_eТ_e', и Т_e > Т_e', возникает связь между колебаниями в соседних областях плазменного объема, объясняемая тем, что при тепловом движении электроны перемещаются и переносят информа­цию. Плазменные колебания в этом слу­чае являются плазменными волнами; эти волны — продольные (v || k, E || k), электростатические (т.е. осциллирует Е-поле, а энергия переменного магнитного поля пренебрежимо мала), их дисперсионное соотношение

= ,

г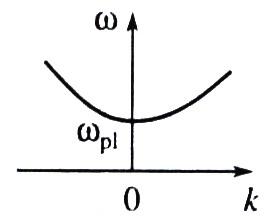де _Te = (2k_BT_e/m_e)^1/2 — тепловая скорость. Частота в этом случае зависит от k, и групповая скорость имеет конечное значение (рис. 2.2).

Рис. 2.2. Дисперсионная кривая для электронных плазменных волн (они же ленгмюровские колебания и волны Бома- Гросса

Плазменные волны существуют при > (рис.2.2). Максимальные фазовая и групповая скорости равны и достигаются при больших k (малых длинах волн ).

Декремент затухания этих волн

= _L + _s, _L = ,

где _L — декремент затухания Ландау, связанный с нели­нейным взаимодействием волн и заряженных частиц, _s — декремент затухания вследствие столкновений. Для слабо­ионизованной плазмы расчет в рамках динамики колебаний тау-приближения дает _s = _ea/2, т.е. в столкновительной плазме плазменные волны быстро затухают.

В сильноионизованной плазме

_s = _ei/2 , _ei =

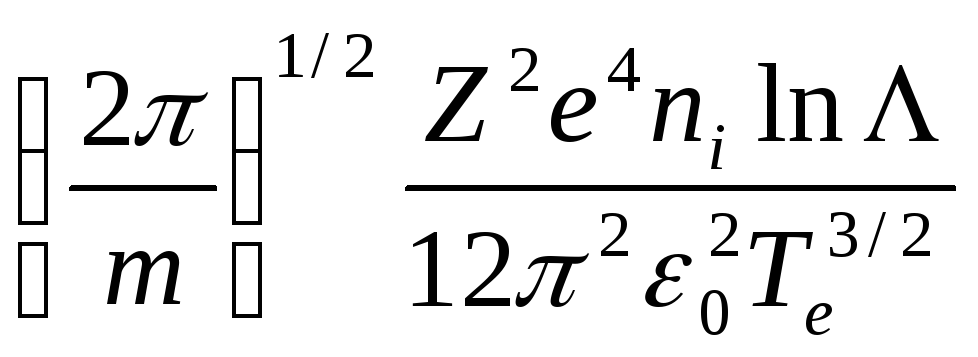
Распространение плазменных колебаний может быть обусловлено также ограниченностью плазменного объема: например, на рис. 2.3 показан плазменный цилиндр, в котором имеются обла­сти с положительными и отрицательными зарядами, создаваемые плазменными

колебаниями. Возникающее на торцах цилиндра электрическое поле приводит к тому, что появляется связь между отдельными слоями среды и возникают плазменные волны.

Рис. 2.3. Схема распространения плазменных колебаний в ограниченной среде, благодаря полям возникающим на границах системы

Волны Ван-Кампена. Волна Ван-Кампена есть моду­лированный пучок частиц, движущийся вместе с поляриза­ционной волной, фазовая скорость которого совпадает со скоростью модулированного пучка. В волнах Ван-Кампена к резонансным частицам, захваченным волной из максвелловской плазмы, добавлены резонансные частицы модули­рованного пучка, компенсирующие затухание Ландау. В том случае, когда плотность модулированного пучка элек­тронов не экспоненциально мала, волны Ван-Кампена за­метно отличаются от ленгмюровских. Именно такие волны принято называть волнами Ван-Кампена в узком смысле этого названия. Спектр собственных продольных высоко­частотных колебаний плазмы состоит из набора ленгмю­ровских волн и волн Ван-Кампена. Такой набор является полным, т.е. любое возмущение (в частности, начальное) можно разложить по этому набору функций.

Звуковые и ионно-звуковые волны. В столкновительной плазме (когда длина волны . l, l — длина сво­бодного пробега), как и в обычном газе, распространяются звуковые волны со скоростью звука _s

= (p₀ /)^1/2 _s

здесь — эффективный показатель адиабаты, p₀, — невозмущенные давление и плотность. В звуковой волне осциллируют концентрация тяжелых частиц (а также элек­тронов вследствие квазинейтральности) и давление газа (плазмы), т.е. эти волны электростатические, ионные, па­раллельные.

В сильноионизованной плазме при нарушении условия > l, т.е. в бесстолкновительном случае, звуковые волны распространяться не могут, однако при Т_е . Т_i импульс может передаваться от слоя к слою электростатическими силами, и тогда распространяются ионно-звуковые волны, в которых из-за квазинейтральности плазмы одновременно смещаются и электроны, и ионы; ионно-звуковые волны продольные (v || k, Е || k), электростатические (осцил­лирует Е-компонента электромагнитного поля). Скорость ионного звука

= (_ek_BT_e /(1 + k²)) / M_i , (2.5)

где _e 1 — эффективный показатель адиабаты неизо­термичной плазмы. В пределе k частота ионно-звуковых колебаний стремится к ионной плазменной частоте _pi = (рис.2.4), а при > _pi на спектре ионно-звуковых колебаний име­ется запрещенная зона (рис.2.4).

Рис. 2.4. Диспер­сионная кривая для ионно- звуковых волн.

Возникшее под действием возмуще­ния локальное увеличение n_i сопрово­ждается ростом n_е (квазинейтральность плазмы), однако вследствие теплового дви­жения электронов возникают разность по­тенциалов (равная k_BТ_е) между областями сгущения и разрежения плазмы и соот­ветствующее электростатическое поле. Ко­лебания ионов происходят под действием возвращающей электростатической силы и сил инерции. Этому механизму соответствует первый член в (2.5); он определяется массой ионов и температурой электронов, т.е. ионно-звуковые волны существуют и при Т_i = 0.

Декремент затухания ионно-звуковых волн в почти бесстолкновительной плазме

= _L + _s,

_L = _,

здесь z — зарядовое число иона, ,— средние тепловые скорости электронов и ионов. В слабоионизован­ной плазме _s = _ia /2, в сильноионизованной — _s = (4/5)_iiT_i /T_e. Можно показать, что декремент затуха­ния мал (т.е. колебания затухают слабо) лишь при условии T_е . Т_i (точнее, Т _е /Т_i >6, 5).

Электромагнитные волны. Выше рассмотрено погло­щение и испускание фотонов при парных (трехчастичных) рассеяниях, в основном сопровождающихся изменением внутреннего состояния частиц плазмы. Ниже рассматри­ваются коллективные процессы в плазме как системе сво­бодных заряженных частиц. В этом случае проявляется не корпускулярная, а волновая природа электромагнитного (ЭМ) излучения. Эти процессы происходят, как правило, при частотах излучения порядка _pi или _ре, что соот­ветствует обычно радио- или ИК-диапазонам.

Как известно, уравнения Максвелла имеют решения, соответствующие электромагнитным (т.е. одновременно ос­циллируют Е- и В-поля) поперечным (Ek, Bk) вол­нам (фазы и частоты колебаний Е и В совпадают, причем ЕВ). В вакууме = k² c² и фазовая скорость равна скорости света с.