ПЛАНАРНЫЕ ГРАФЫ

Граф называют планарным, если существует такое изображение на плоскости его вершин и ребер, что

•каждая вершина изображается отдельной точкой на плоскости и

Задача определения того, можно ли изобразить граф на плоскости без пересечения ребер, имеет большой практический интерес, например, при конструировании интегральных схем или печатных плат необходимо выяснить, можно ли окончательную схему вложить в плоскость.

Наиболее успешный подход к определению планарности состоит в том, что граф разбивается на подграфы и затем делается попытка разместить его на плоскости, добавляя подграфы один за другим и сохраняя при размещении планарность.

Планарные графы

Пусть задан неориентированный граф G = (V,E).

Каждой вершине vi из V сопоставлена точка ai в некотором евклидовом пространстве, где ai aj при i j.

Каждому ребру e = (vi, vj) из E сопоставлена непрерывная кривая L, соединяющая точки ai и aj и

неТогдапроходящаяесли всечерезкривые,другиесоптоставленныечки a . ребрам

k

графа, не имеют общих точек, кроме концевых, то это множество точек и кривых называется

геометрической реализацией графа G.

ТЕОРЕМА: Каждый конечный граф G можно реализовать в трехмерном евклидовом пространстве (без пересечения ребер).

Доказательство:

Возьмем в пространстве любую прямую L и разместим на ней все вершины графа G.

Пусть в G имеется q ребер. Проведем q полуплоскостей через L так, чтобы прямая L была их общим ребром (типа тетрадки).

После этого каждое ребро графа G можно изобразить линией в своей полуплоскости и они, очевидно, не будут пересекаться.

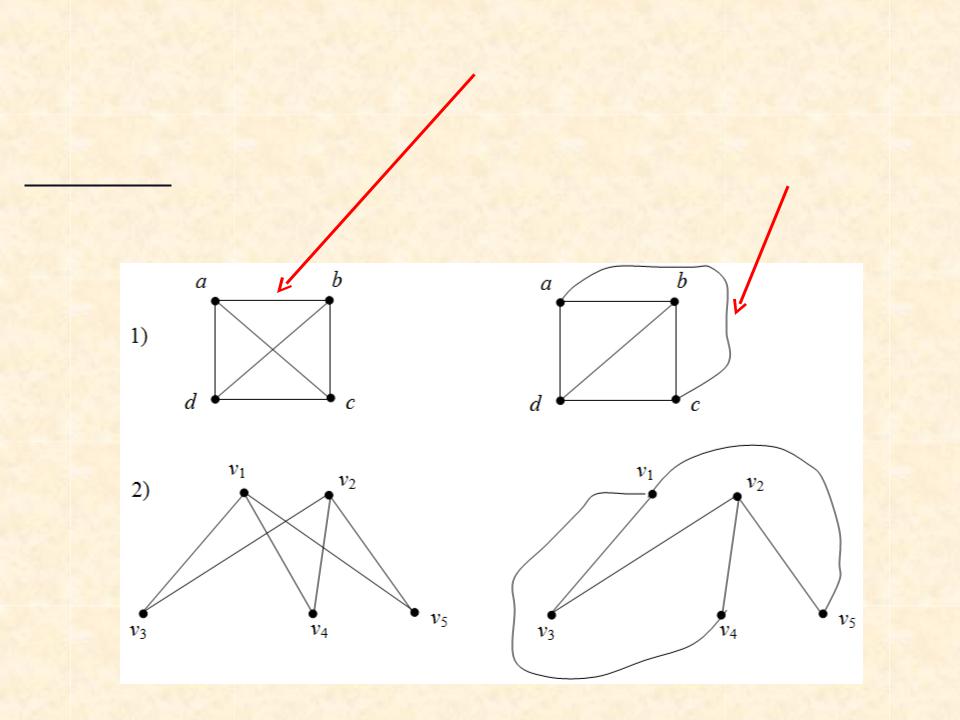
Граф называется планарным, если существует его планарная реализация, то есть геометрическое представление на плоскости без пересечения ребер (имеет плоскую укладку, представим

плоским графом).

ПРИМЕР соответствия плоского графа кубу

Поскольку орграф планарен тогда и только тогда, когда планарен соответствующий неориентированнный граф, то достаточно рассматривать только неориентированные графы.

Так как параллельные ребра и петли всегда можно добавить или

удалить без нарушения планарности. то достаточно рассматривать

только простые графы (неориентированные, простые и двусвязные)

Можно нарисовать полный граф на плоскости с 4-мя вершинами без пересечения ребер, следовательно неплоский граф должен иметь по крайней мере 5 вершин. Аналогично неплоский граф

должен иметь по крайней мере 9 ребер.

В общем случае используют теорему Эйлера.

Непересекающиеся части плоскости, заключённые между циклами, образованными ребрами планарного графа, называются гранями графа (одна из граней бесконечна, она называется

внешней гранью).

Границей грани называется множество вершин и ребер, принадлежащих этой грани.

Теорема (Эйлера) Если G – связный планарный граф, содержащий v вершин, e ребер и f граней, тоv e f 2

Доказательство.

Пусть G – связный планарный граф, который имеет k вершин. Рассмотрим некоторый остов этого графа. Остов имеет всего одну внешнюю грань f=1, v=k вершин и e=k-1

ребер, т.е.

v - e + f = k - (k - 1) + 1 = 2.

Будем поочередно добавлять к остову недостающие ребра графа G. При каждом добавлении число вершин не изменится, число ребер увеличивается на единицу, так же

как и число граней, поскольку при добавлении к остову ребра, связывающего две несмежные вершины, получается цикл, разделяющий текущую грань на две.

Таким образом, формула будет верна для всякого графа,

получающегося в результате таких операций, а поскольку

графом G заканчивается вся эта процедура, то эта формула

будет верна и для него.

Графы Понтрягина - Куратовского, играют важную роль в теории планарности графов. Они

не являются планарными графами.

ТЕОРЕМА ПОНТРЯГИНА – КУРАТОВСКОГО:

Для того, чтобы граф был планарный, необходимо и достаточно, чтобы он не мог содержать в себе в качестве подграфов граф К33

или К5.

Следствие:

Графы Кn, где n≥5, не являются планарными (не допускают плоскую укладку)