7. Основные понятия теории графов

7.1. Графы и орграфы.

Теория графов – это раздел дискретной математики, изучающий объекты, представимые в виде отдельных элементов (вершин) и связей между ними (дуг, рёбер).

Теория графов берет начало с решения задачи о кенигсбергских мостах в 1736 году знаменитым математиком Леонардом Эйлером (1707-1783: родился в Швейцарии, жил и работал в России).

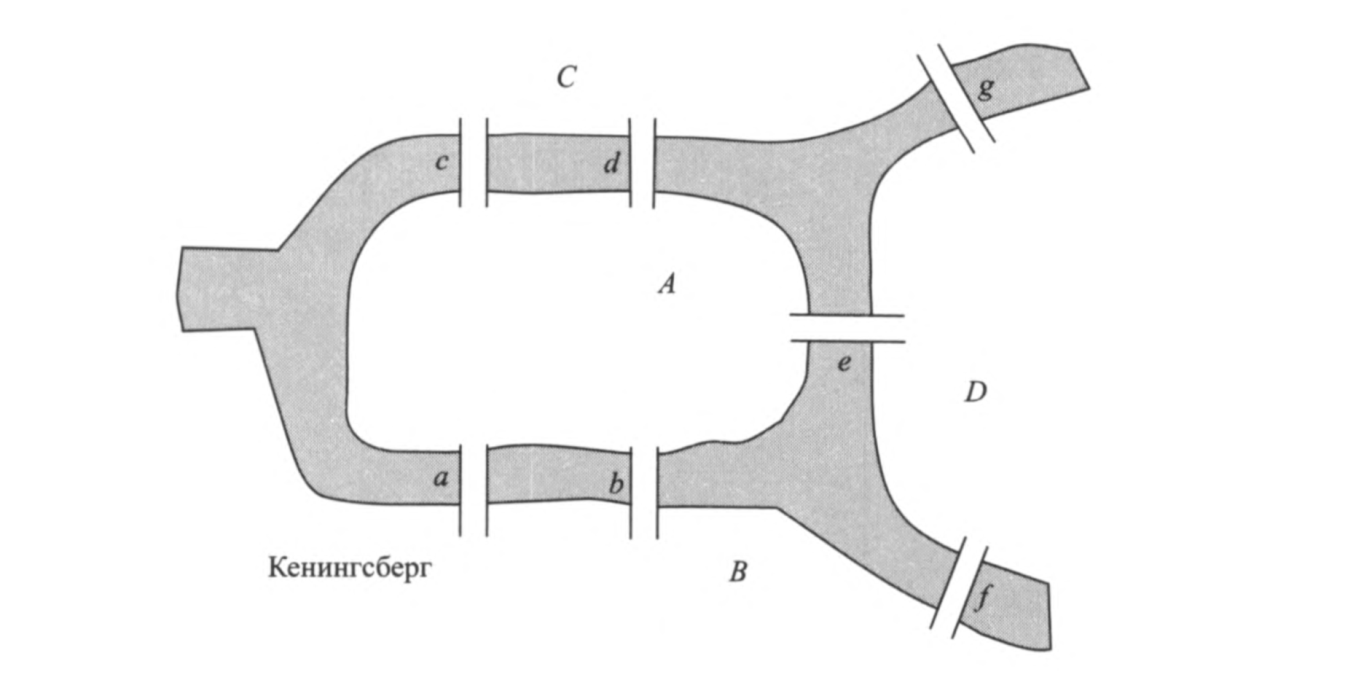
Задача о кенигсбергских мостах.

В прусском городке Кенигсберг на реке Прегал семь мостов. Можно ли найти маршрут прогулки, который проходит ровно 1 раз по каждому из мостов и начинается и заканчивается в одном месте?

Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется Эйлеровым графом.

Последовательность вершин (может быть с повторением), через которые проходит искомый маршрут, как и сам маршрут, называется Эйлеровым циклом.

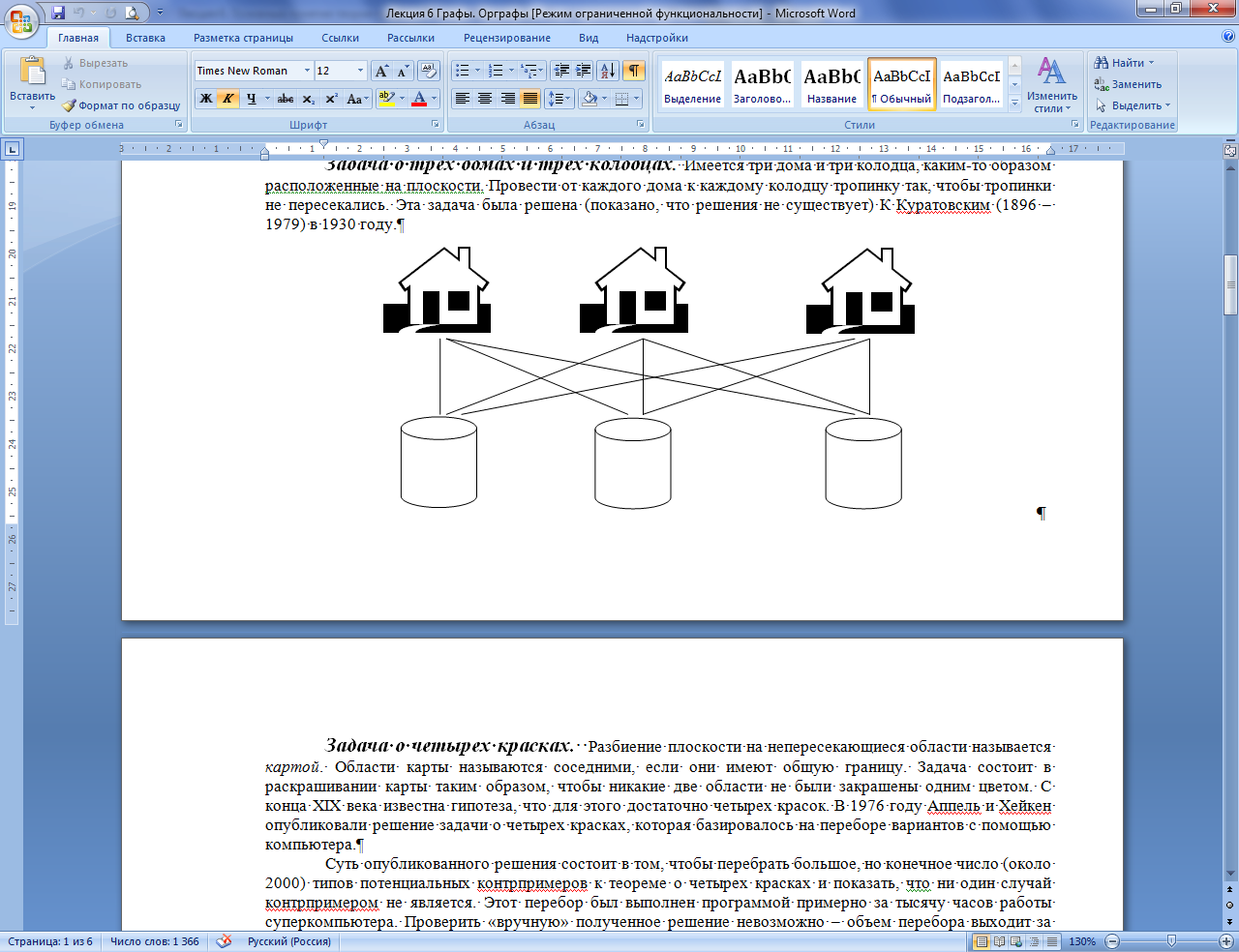
Задача о трех домах и трех колодцах.

Имеется три дома и три колодца, каким-то образом расположенные на плоскости. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эта задача была решена (показано, что решения не существует) Куратовским (1896 – 1979) в 1930 году.

Задача о четырех красках. Разбиение плоскости на непересекающиеся области называется картой. Области карты называются соседними, если они имеют общую границу. Задача состоит в раскрашивании карты таким образом, чтобы никакие две соседние области не были закрашены одним цветом. С конца XIX века известна гипотеза, что для этого достаточно четырех красок. Гипотеза не доказана до сих пор.

В 1976 году Аппель и Хейкен опубликовали решение задачи о четырех красках, которая базировалось на переборе вариантов с помощью компьютера.

Суть опубликованного решения состоит в том, чтобы перебрать большое, но конечное число (около 2000) типов потенциальных контрпримеров к теореме о четырех красках и показать, что ни один случай контрпримером не является. Этот перебор был выполнен программой примерно за тысячу часов работы суперкомпьютера.

Проверить «вручную» полученное решение невозможно – объем перебора выходит за рамки человеческих возможностей. Многие математики ставят вопрос: можно ли считать такое «программное доказательство» действительным доказательством? Ведь в программе могут быть ошибки…

Таким образом, остается уповать на программистскую квалификацию авторов и верить, что они все сделали правильно.

Определение 7.1. Графом G=G(V, E) называется совокупность двух конечных множеств: V – называемого множеством вершин и множества E пар элементов из V, т.е. EÍV´V, называемого множеством рёбер, если пары неупорядочены, или множеством дуг, если пары упорядочены.

В первом случае граф G(V,E) называется неориентированным, во втором – ориентированным.

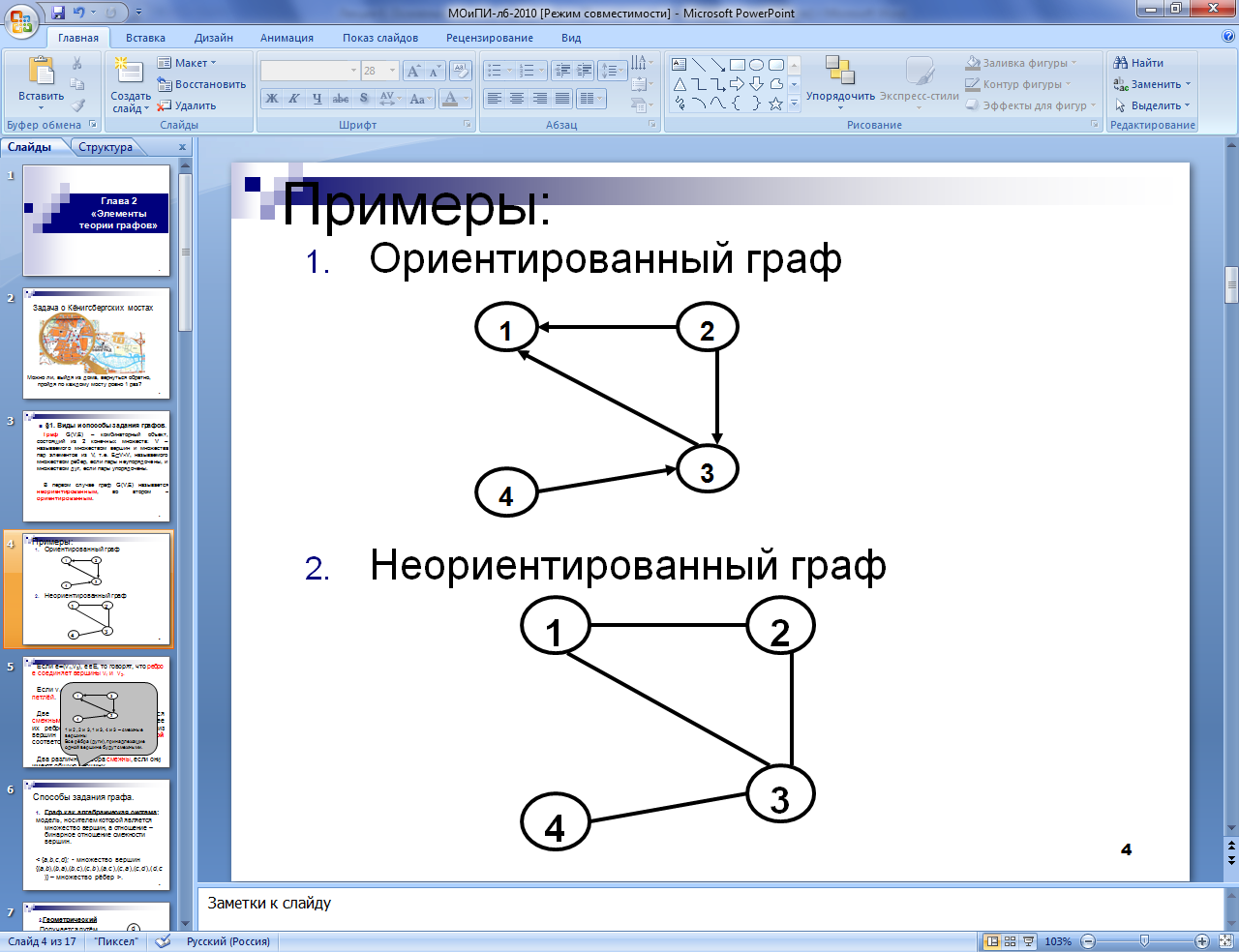
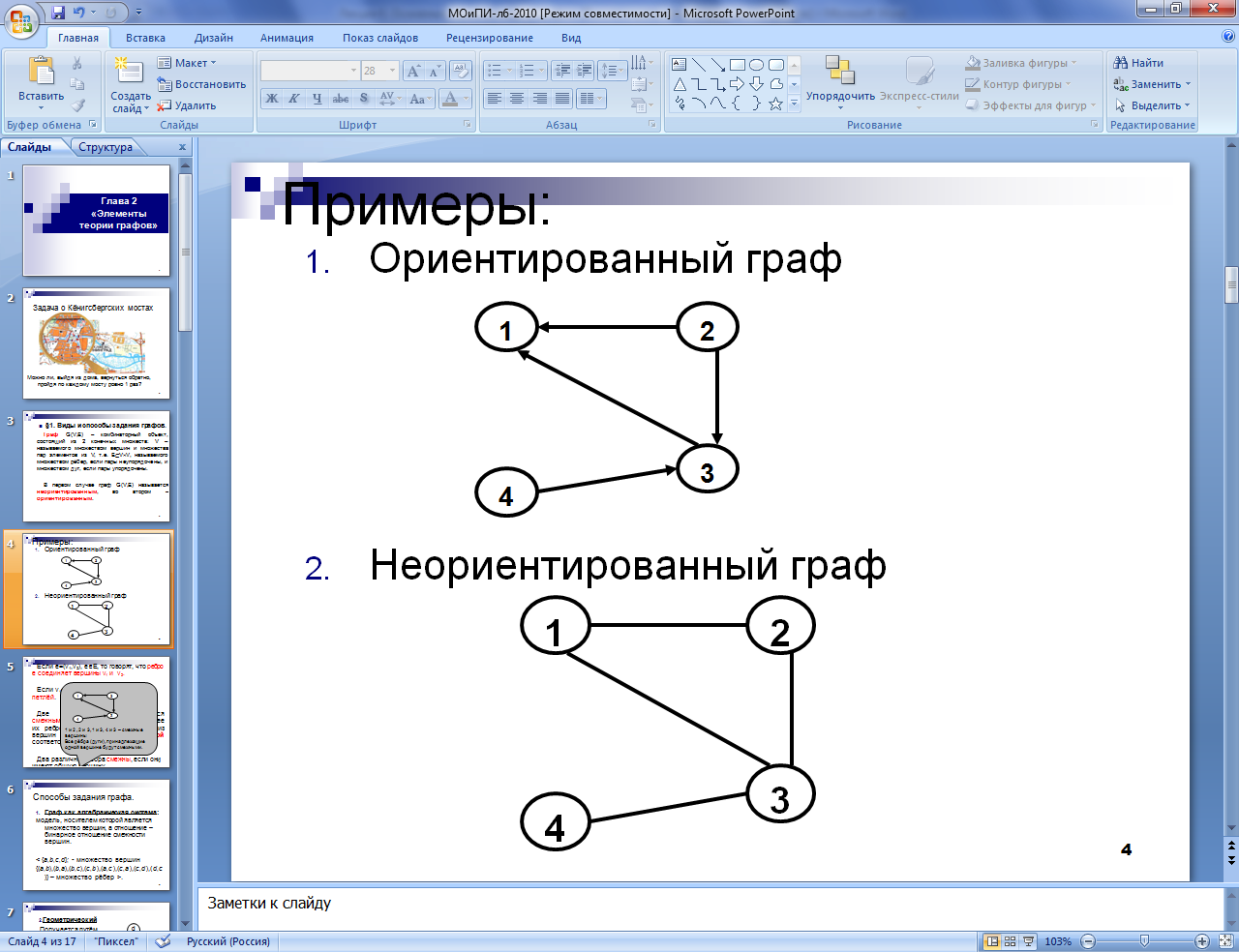
ПРИМЕР . Граф с множеством вершин V = {а,b,с} и множеством ребер Е ={{а, b}, {b, с}}

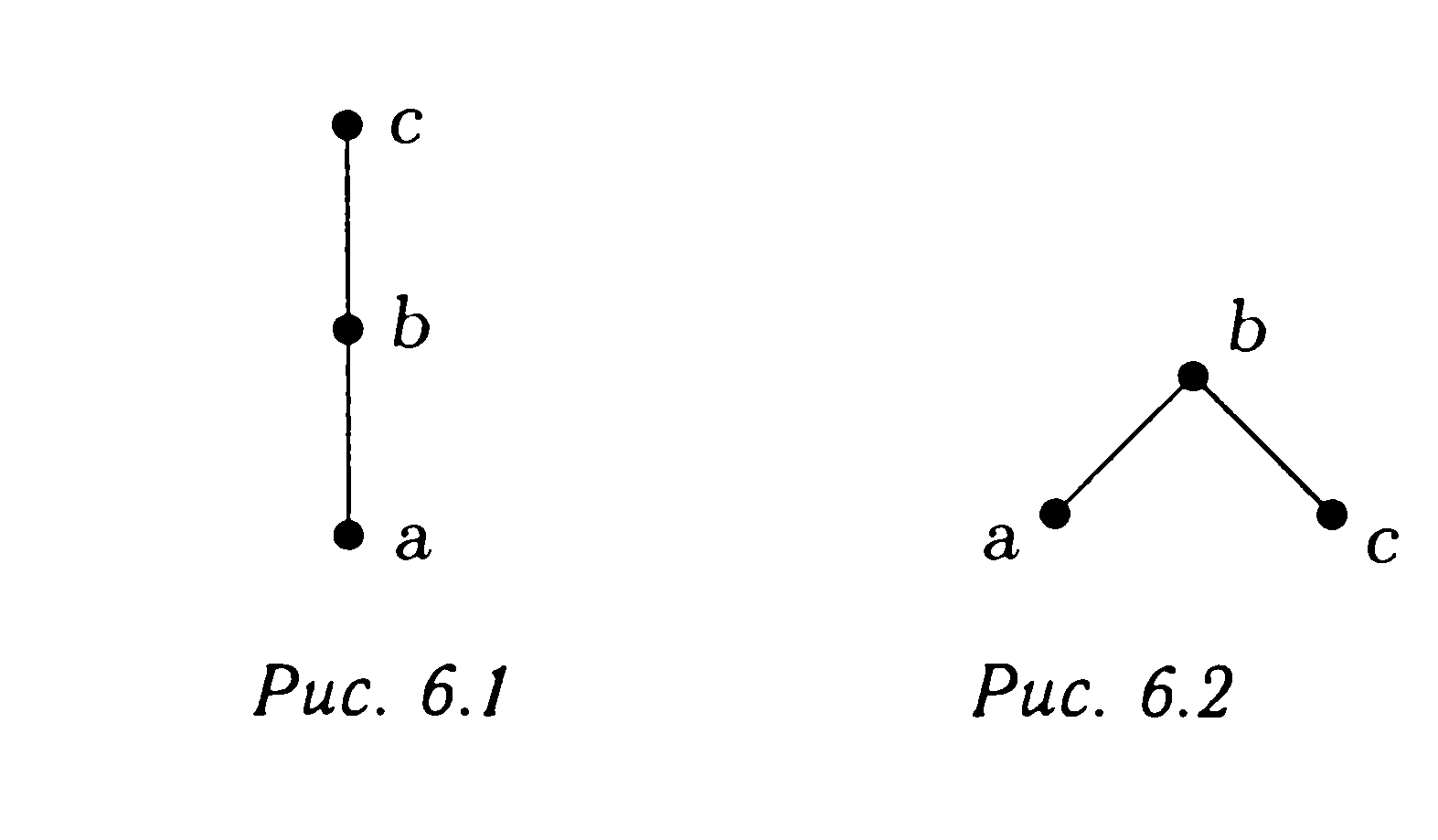
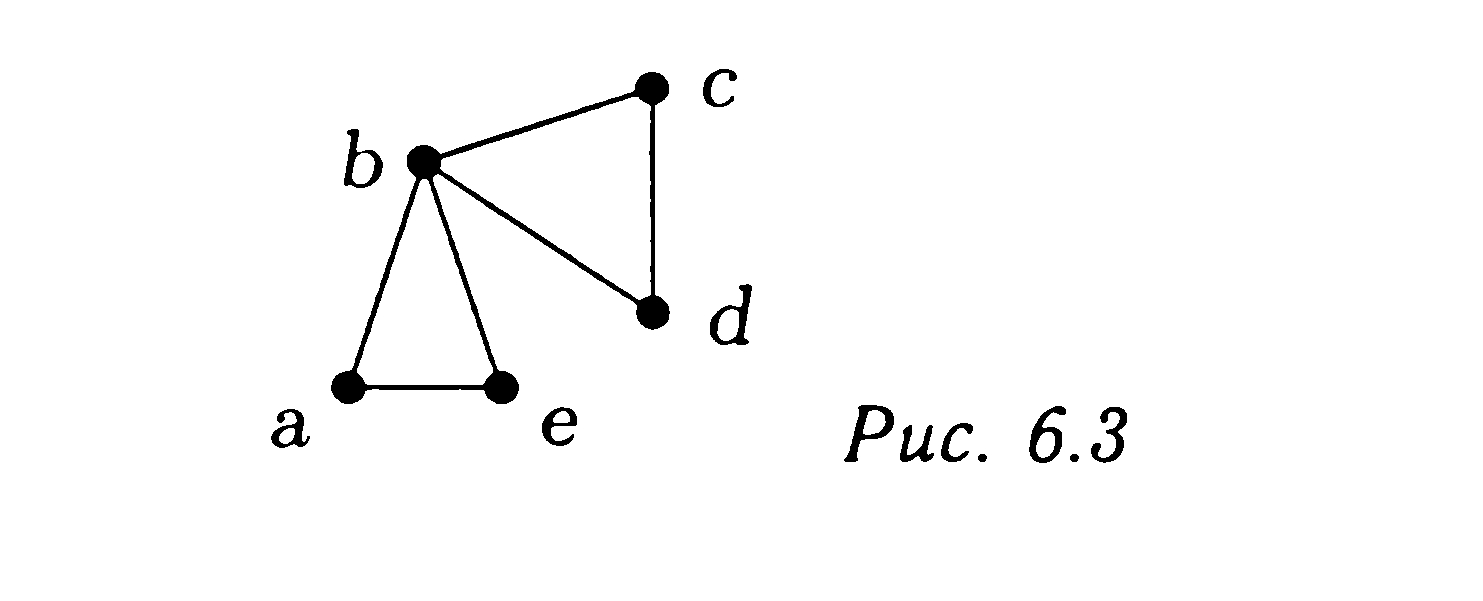
ПРИМЕР. Граф, у которого V = {a,b,c,d,e} и Е = {{а, b}, {а, е}, {b, е}, {b, d}, {b, с}, {с, d}},

Если e=(v₁,v₂), еÎЕ, то говорят, что ребро е соединяет вершины v₁ и v₂.

Две вершины v₁,v₂ называются смежными, если существует соединяющее их ребро. В этой ситуации каждая из вершин называется инцидентной соответствующему ребру.

Два различных ребра смежны, если они имеют общую вершину. В этой ситуации каждое из ребер называется инцидентным соответствующей вершине.

Число вершин графа G обозначим v, а число ребер - e:

.

Геометрическое представление графов следующее:

1) вершина графа – точка в пространстве (на плоскости);

2) ребро неориентированного графа – отрезок;

3) дуга ориентированного графа – направленный отрезок.

Определение 7.2. Если в ребре e=(v₁,v₂) имеет место v₁=v₂ , то ребро е называется петлёй. Если в графе допускается наличие петель, то он называется графом с петлями или псевдографом.

Если в графе допускается наличие более одного ребра между двумя вершинами, то он называется мультиграфом.

Если каждая вершина графа и (или) ребра помечена, то такой граф называется помеченным (или нагруженным). В качестве пометок обычно используются буквы или целые числа.

Определение 7.3. Граф G(V, E) называется подграфом (или частью) графа G(V,E), если V V, E E. Если V=V, то G называется остовным подграфом G.

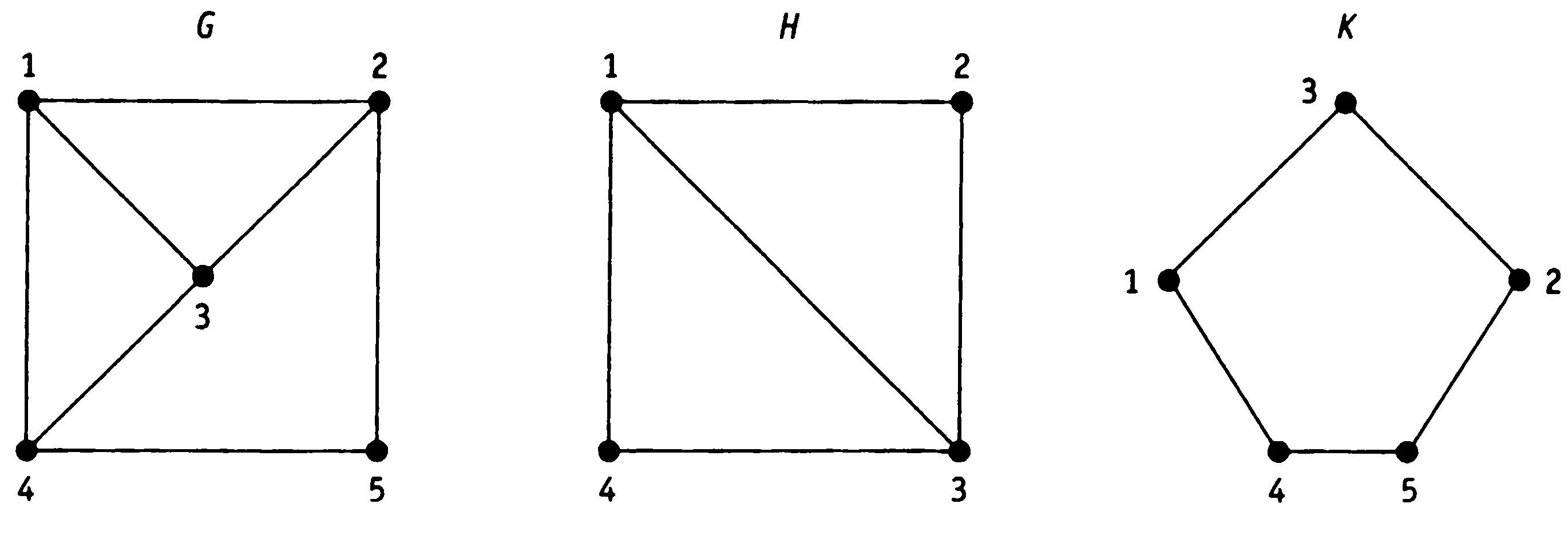
Пример 7.1. Дан неориентированный граф.

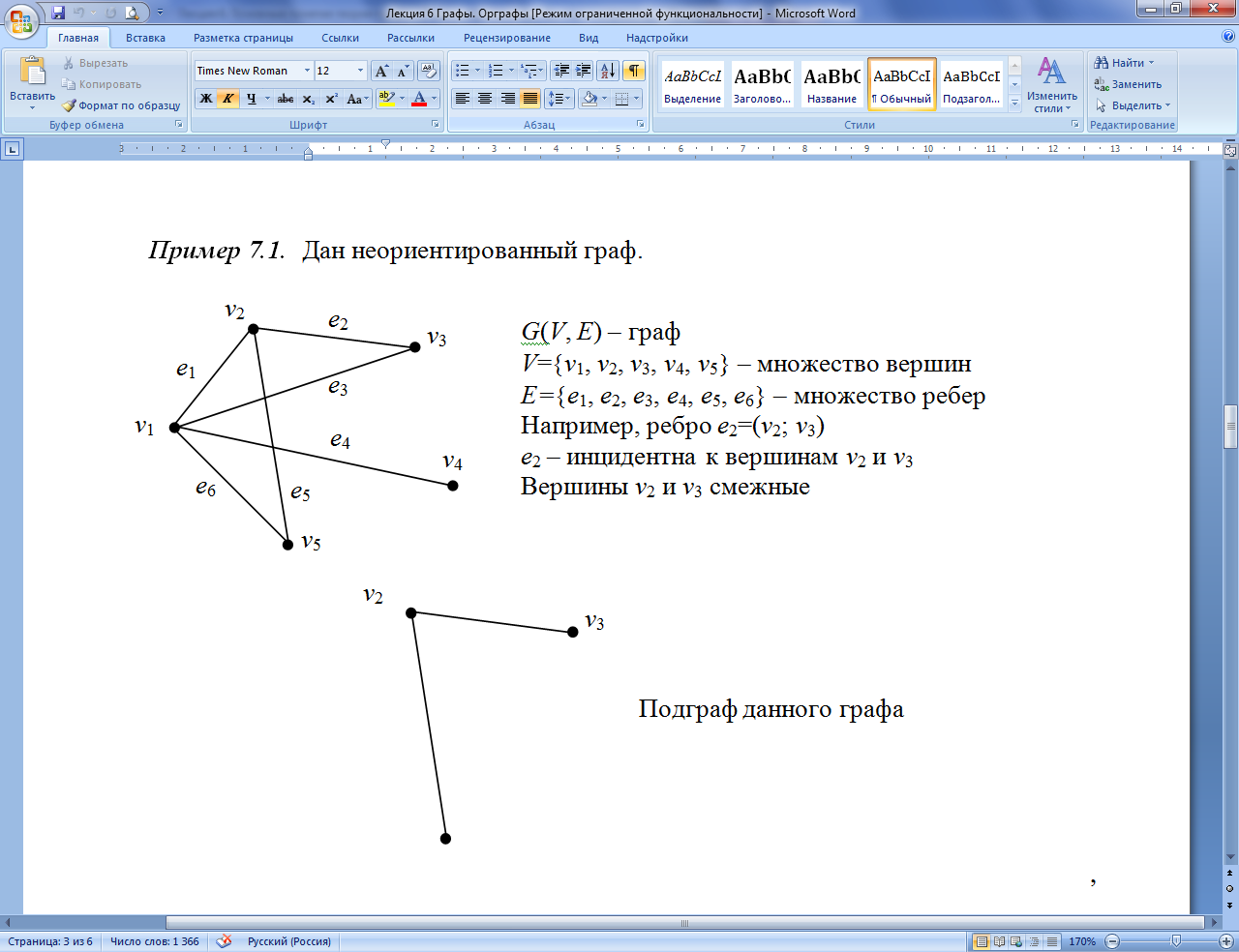
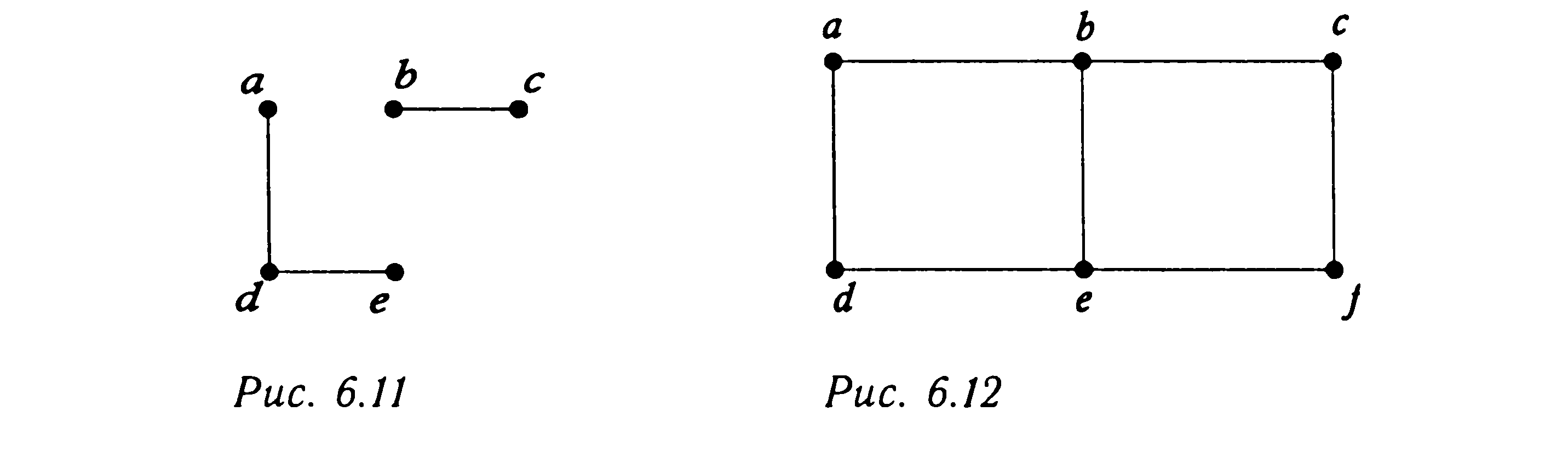
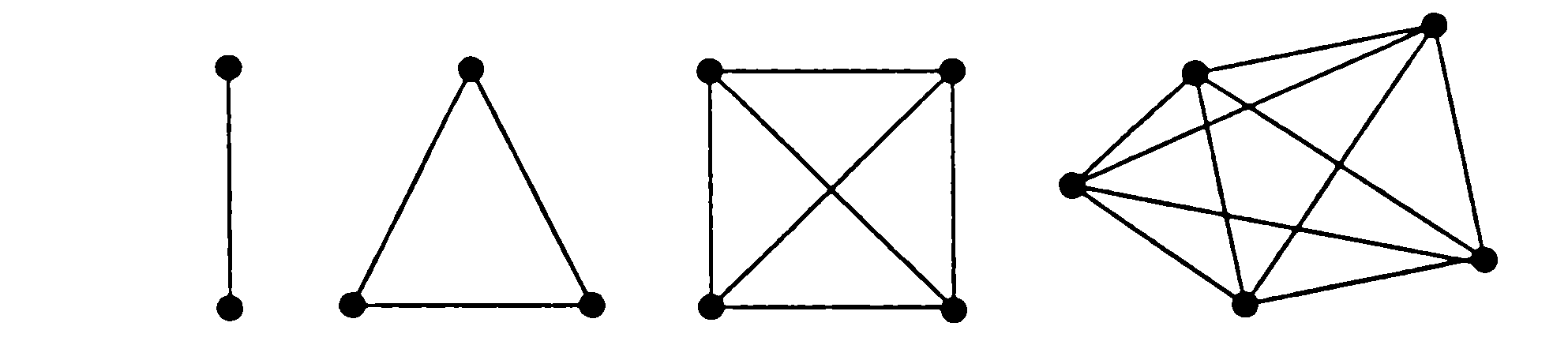
Определение 7.4. Граф называется полным, если любые две его вершины соединены ребром. Полный граф с n вершинами обозначается через K_n.

Графы К₂, К_3, К₄ и К₅.

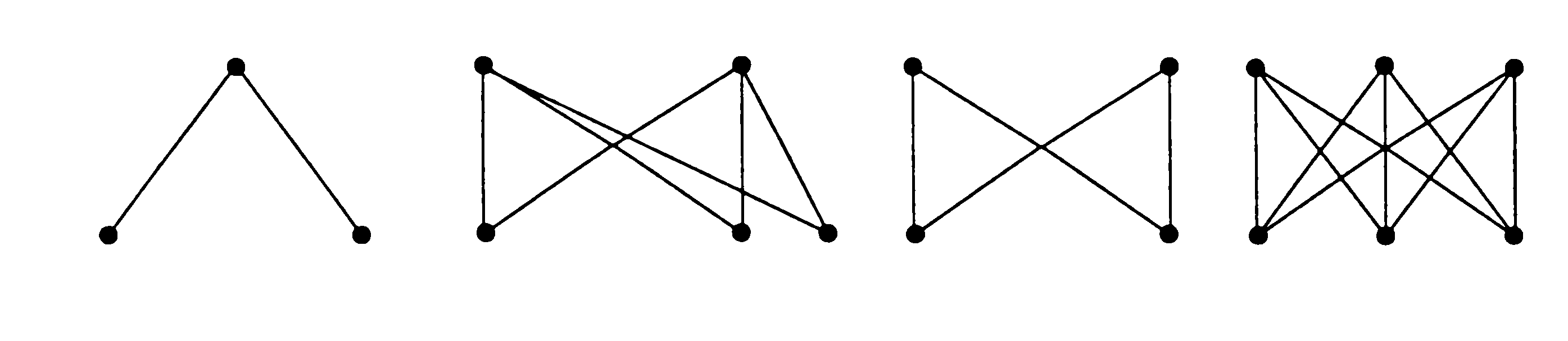
Определение 7.5. Граф G=G(V, E) называется двудольным, если V можно представить как объединение непересекающихся множеств, скажем V=AB, так что каждое ребро имеет вид (v_i, v_j), где v_iA и v_jB.

Каждое ребро связывает вершину из А с вершиной из В, но никакие две вершины из А или две вершины из В не являются связанными.

Двудольный граф называется полным двудольным графом K_{m, n}, если A содержит m вершин, B содержит n вершин и для каждого v_iA, v_jB имеем (v_i, v_j)E.

Таким образом, для каждого v_iA, и v_jB имеется связывающее их ребро.

K₁₂ K₂₃ K₂₂ K₃₃

Пример 7.2. Построить полный двудольный граф K_2,4 и полный граф K₄.

Граф единичного n-мерного куба В_n .

Вершины графа - n-мерные двоичные наборы. Рёбра соединяют вершины, отличающиеся одной координатой.

Пример: