3.3 Отношение эквивалентности. Отношение частичного порядка.

Определение 3.6. Отношение  на A есть отношение эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Отношение эквивалентности ab часто обозначается: a  b.

Пример .. Отношение равенства на множестве целых чисел есть отношение эквивалентности.



Пример .. Отношение «одного роста» есть отношение эквивалентности на множестве людей X.

Пример .. На множестве натуральных чисел можно определить отношение эквивалентности, считая числа a и b эквивалентными, если их сумма чётна.

1. (а + а) – всегда чётна Þ оно рефлексивно;

2. (а + b) = (b + а) Þ оно симметрично;

3. Если (а + b) и (b + с) - чётные числа, то а + с = (а + b) + (b + с) – 2b – также чётно

ß

R – транзитивно

Эквивалентные элементы, т.е. находящиеся в отношении эквивалентности, обладают какими-то общими признаками.

Если на множестве задано отношение эквивалентности, то все его элементы можно естественным способом разбить на непересекающиеся подмножества.

Все элементы в любом из таких подмножеств эквивалентны друг другу в прямом смысле. Наличие такого разбиения – движущая сила любой классификации.

Определение 3.8. Пусть R – отношение эквивалентности на множестве А. Определим класс эквивалентности, содержащий элемент аÎА (обозначение R[a]), как множество элементов из А, находящихся в отношении R с элементом а, т.е

R[a] = {x| xÎA и xRa}

Теорема 3.2(основное свойство классов эквивалентности):

Отношение эквивалентности R разбивает множество А на попарно непересекающиеся классы эквивалентных элементов таким образом, что каждый элемент А принадлежит точно одному классу эквивалентности.

Определение 3.9. Если R – отношение эквивалентности, то число классов эквивалентности называется рангом отношения R.

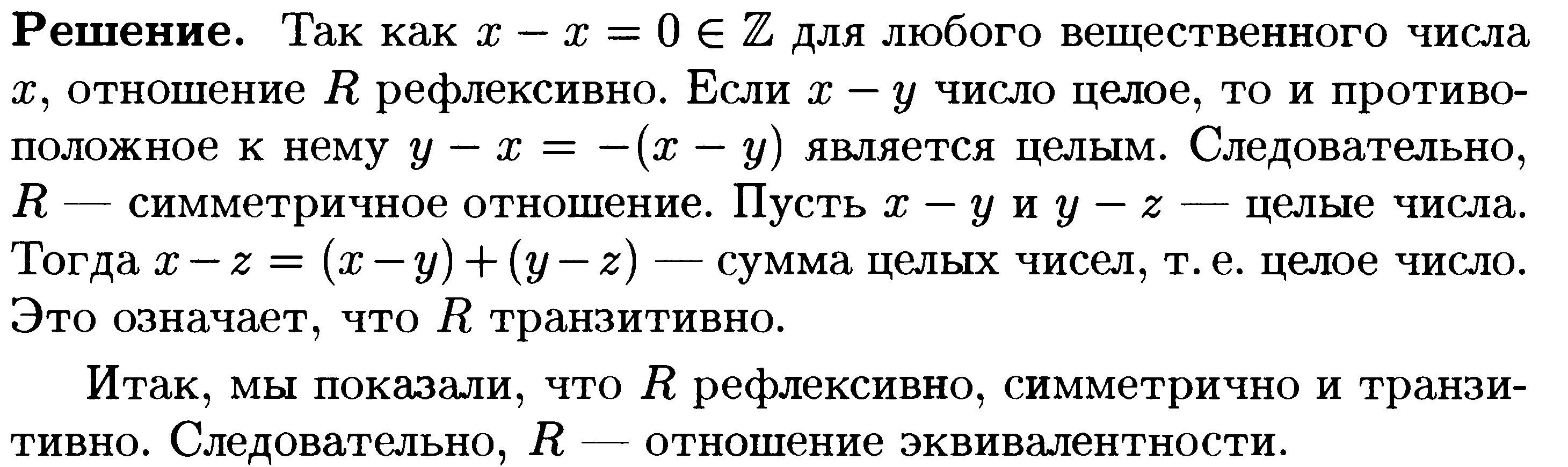
Класс эквивалентности произвольного вещественного числа x определяется по формуле

R[x] = {z| zÎR и z-x-целое число} или E_x

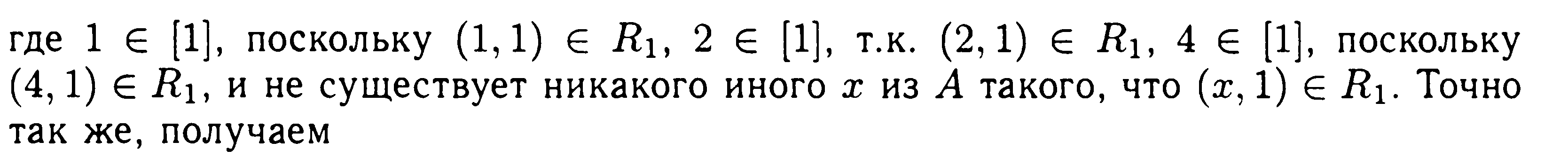
Множество всех классов эквивалентности множества А по отношению R равно

Определение 3.7. Отношение  на A есть отношение частичного порядка, если оно рефлексивно, антисимметрично и транзитивно и обозначается символом .

Частичный порядок важен в тех ситуациях, когда мы хотим как-то охарактеризовать старшинство.

Иными словами, решить при каких условиях считать, что один элемент множества превосходит другой.

Пример .. Отношение xy на множестве действительных чисел есть отношение частичного порядка.

Пример .. Во множестве подмножеств некоторого универсального множества U отношение AB есть отношение частичного порядка.

Пример .. Схема организации подчинения в учреждении есть отношение частичного порядка на множестве должностей.

Множества с частичным порядком принято называть частично упорядоченными множествами.

Если R – отношение частичного порядка на множестве А, то при x≠y и xRy мы называем x предшествующим элементом, а y последующим.

У произвольного взятого элемента y может быть много предшествующих элементов.

Однако, если x предшествует y, и не существует таких элементов z , для которых xRz и zRy, мы называем x непосредственным предшественником y и пишем xy.

Непосредственных предшественников можно изобразить с помощью графа, известного как диаграмма Хассе.

Вершины графа изображают элементы частично упорядоченного множества А, и если xy, то вершина x помещается ниже вершины y и соединяется с ней ребром.

Диаграмма Хассе выдаст полную информацию об исходном частичном порядке, если подняться по всем цепочкам ребер.

Линейным порядком на множестве А называется отношение частичного порядка, при котором, из любой пары элементов можно выделить предшествующий и последующий.

Различные сортирующие процедуры в информатике требуют, чтобы элементы сортируемых множеств были линейно упорядочены. В этом случае они могут выдавать упорядоченный список.

Другие приложения используют частичный порядок. Предполагая, что в любом частично упорядоченном множестве найдется минимальный элемент (не имеющий предшественников), и максимальный (не имеющий последующих элементов).

Определение 3.10. Отношение  на A есть отношение толерантности, если оно рефлексивно и транзитивно.

Пример .4. Пусть Н – произвольное множество,

В₁(Н) – множество непустых подмножеств множества Н.

Определим отношение R на элементах множества В₁(Н) условием

xRy Û x Ç y ¹ Æ, x,yÎ В₁(Н)

Симметричность и рефлексивность данного отношения очевидны, поэтому оно будет отношением толерантности.