§3. Системы массового обслуживания с ожиданием

Рассмотрим систему массового обслуживания с каналами и неограниченной очередью, в которой заявки не покидают очереди, т.е. чистую систему с ожиданием. Поскольку в этом случае, в формулах (4) и (6) необходимо положить, в результате чего из (4) получим:

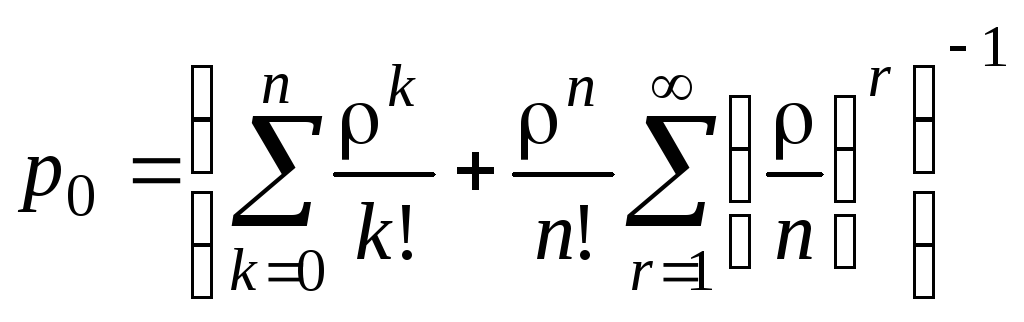. (10)

Как уже отмечалось, условие существования стационарного режима системы обслуживания совпадает с условием сходимости ряда в (10):

. (11)

Смысл неравенства (11) ясен: среднее число заявок, приходящих в систему за среднее время обслуживания одной заявки, должно быть меньшим числа каналов обслуживания. Если это условие не выполняется, то очередь неограниченно возрастает и стационарный режим не наступает.

Будем считать, что условие (11) выполнено и с помощью формулы суммы геометрической прогрессии из (10) найдем:

. (12)

Кроме того, запишем (5) и (6) при :

,; (13)

,. (14)

Определим теперь основные характеристики рассматриваемой системы обслуживания.

1. Среднее число занятых каналовпроще всего найти по формуле (1):. В системе обслуживания с неограниченной очередью при условии (11), поэтому

. (15)

В справедливости равенства (15) можно убедиться непосредственно, с использованием формул (12) - (14):

=.

2. Среднее число заявок в очереди найдем с помощью (14):

3. Среднее число заявок в системеравно сумме среднего числа занятых каналови средней длины очереди:.

4. Среднее время пребывания заявки в системенаходим по формуле Литтла (2):.

5. Среднее время ожидания заявки в очередиможно найти по формуле Литтла (3):.

Пример 4.

В порту работают три причала для разгрузки судов. В сутки в порт прибывают в среднем 8 судов с грузом. Среднее время разгрузки одного судна составляет 8 часов. Найти показатели эффективности системы разгрузки судов.

В данном случае интенсивности потоков заявок и обслуживаний равны, соответственно:,, приведенная плотность потока заявок=, число каналов обслуживания. Согласно (12). Поэтому:

1. среднее число занятых каналов ;

2. среднее число заявок в очереди ;

3. среднее число заявок в системе;

4. среднее время пребывания заявки в системе ;

5. среднее время ожидания заявки в очереди .

Заметим, что рассмотренная система массового обслуживания работает с заметной перегрузкой: из трех причалов заняты в среднем 2,67, в очереди со средней длиной более 6 судов приходится ожидать в среднем около суток, а находиться в порту - более суток.

§4. Системы массового обслуживания с ограниченной очередью

Рассмотрим систему массового обслуживания с каналами и ограничением на длину очереди: она не может превышатьзаявок. В такой системе заявка, поступившая в момент, когда все каналы обслуживания заняты и в очереди находятсятребований, получает отказ. Как отмечалось в конце§1, уравнения (4) - (6) в этом случае принимают вид

; (16)

,; (17)

,. (18)

Для чистойсистемы массового обслуживания (заявки не покидают очереди, т.е., значит) соотношения (16) - (18) упрощаются:

; (19)

,; (20)

,. (21)

Найдем основные характеристики такой системы.

1. Вероятность отказав обслуживании заявки;

2. относительная пропускная способность;

3. абсолютная пропускная способность ;

4. среднее число занятых каналовнайдем по формуле (1):;

5. среднее число заявок в очереди

=;

6. среднее число заявок в системе;

7. среднее время пребывания заявки в системе находим по формуле (2):;

8. среднее время ожидания заявки в очереди , см. (3).

Пример 5.

На одноканальный телефонный коммутатор поступает в среднем 30 вызовов в час. Средняя длительность разговора составляет 2,5 минуты. Если в момент очередного вызова канал связи занят, этот вызов может быть поставлен в очередь. Число заявок в очереди не превышает трех. Если в очереди находятся три заявки, то поступающие вызовы не обслуживаются.

Найти характеристики эффективности данной системы массового обслуживания.

В этом случае интенсивности потоков заявок и обслуживаний равныисоответственно, приведенная плотность потока заявок, число каналов обслуживания, максимальная длина очереди. Из (19) - (21) получаем:,,,,. Отсюда находим:

1. вероятность отказа;

2. относительная пропускная способность;

3. абсолютная пропускная способность;

4. среднее число занятых каналов;

5. среднее число заявок в очереди;

6. среднее число заявок в системе;

7. среднее время пребывания заявки в системе ;

8. среднее время ожидания заявки в очереди .

10