11 (2). Простейшие задачи квантовой механики. Линейный гармонический осциллятор

Гармоническим осциллятором называется частица, совершающая гармонические колебания. Потенциальная энергия равна

(11.1)

поэтому уравнение Шредингера принимает вид: (11.2)

Качественно задача подобна рассмотренной выше задаче о движении частицы в потенциальной яме, однако здесь имеется особенность, из-за которой задача довольно сильно усложняется: в пределах ямы потенциальная энергия не имеет постоянного значения, а изменяется по параболическому закону.

Обозначим: (11.3) Тогда уравнение Шредингера

принимает вид: (11.4)

Будем искать решение в виде (11.5)

Тогда для функции vполучаем следующее уравнение: (11.6)

Будем искать функциюvв виде бесконечного степенного ряда:

(11.7)

Для того, чтобы решение не обратилось в бесконечность, коэффициенты этого ряда надо подобрать так, чтобы они были равны нулю, начиная с некоторого номераn+1. (Другими словами, бесконечный ряд должен превратиться в полином степениn).

Подставим (11.7) в (11.6):

Приравнивая нулю сумму коэффициентов при одинаковых степенях, получаем следующие рекуррентные соотношения для коэффициентов ak:

(11.8) Как видно из этого соотношения, для того, чтобы an¹0, аan+2 = 0,

необходимо, чтобыln= 2n+1 (11.9)

Отсюда и из формулы (11.3) находим энергию осциллятора: (11.10) в частности, приn= 0 минимальная энергия осциллятора не равна нулю:

(11.11)

что согласуется с соотношениями неопределенности. Энергия E0 называется "нулевой энергией"; она не исчезает даже когда температура стремится к абсолютному нулю.

Рекуррентная формула (11.8) позволяет последовательно вычислить все члены ряда. Функциюvможно теперь записать в виде: еслиnчетное

еслиnнечетное

Эти полиномы называются полиномами Эрмитаи обозначаются . Таким образом, волновая функцияYn, принадлежащая собственному значениюEn, выражается формулой

(11.12)

Коэффициенты Cnнаходятся из условия нормировки:

Вычисления дают следующий результат:

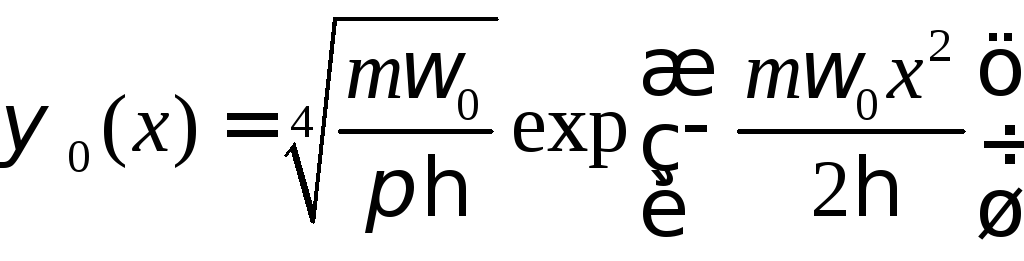(11.13)

В частности, для нулевого состояния собственная функция имеет вид:

15