9 (2). Простейшие задачи квантовой механики. Частица в "потенциальной яме" ("ящике")

Одномерная прямоугольная потенциальная яма ("ящик") (рис20)

Так называется одномерная область, в которой потенциальная энергия имеет вид, изображенный на (рис20). Для этой области легко получить точное решение уравнения Шредингера и рассмотреть задачу о квантовании энергии.

Потенциальная энергия равна нулю на дне ямы ("ящика"), и равна U0 вне стенок "ящика".

Одномерная прямоугольная потенциальная яма (ящик) с бесконечно высокими стенками (рис21).

Наиболее простым в математическом отношении является решение для потенциальной ямы с бесконечно высокими стенками. Иногда ее называют ямой с идеально отражающими стенками.

Ширина ямы (ящика) равна L, на дне ямы потенциальная энергия равна нулю, высота стенок бесконечно велика.

В этом случае внутри ямы частица движется свободно, но выйти за ее пределы не может, т.е. за пределами ямы волновая функция должна обратиться в нуль. Но волновая функция должна быть непрерывна, поэтому она должна быть равна нулю в точках x = 0 и x = L:(9.1) - это граничные условия для волновой функцииY.

Стационарное уравнение Шредингера (8.6)

внутри ямы принимает вид (т.к. U= 0): (9.2)

Общее решение этого уравнения хорошо известно: (9.3)

Из условия (9.1) Y(0) =0 следует, чтоB= 0.

Из второго граничного условия Y(L) =0 следует, что откуда или

(9.4) гдеn = 1, 2, 3, ... - целое число

Таким образом, собственными функциями уравнения Шредингера в рассматриваемой задаче являются волновые функции вида (9.5)Собственные значения энергии найдем из формулы (9.4): - дискретный спектр собственных значений энергии.

Таким образом, частица (например, электрон) в потенциальной яме может иметь не произвольные, а лишь дискретные, квантованные значения энергии.

Рассмотрим некоторые свойства собственных функций.

1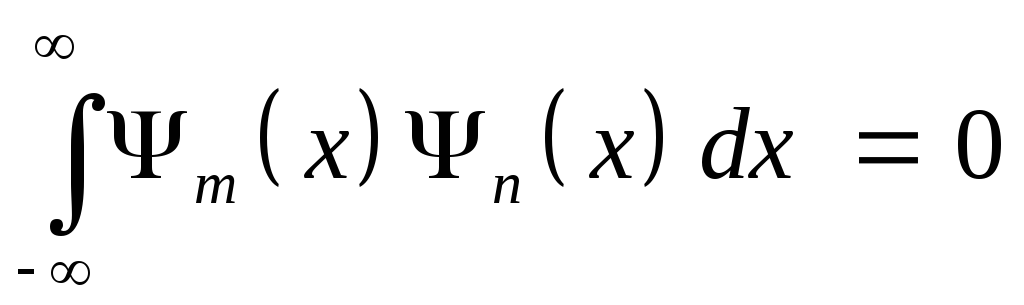). Собственные функции, принадлежащие различным собственным значениям, ортогональны, т.е.

Доказательство (9.7)

если m≠n

Если m=n, то интеграл (9.7) не равен 0, и из условия нормировки можно найти коэффициентAn:

т.е. нормирующий множитель у всех собственных функций одинаков. Поэтому (9.8)

Графики первых трех собственных функций(рис22) Плотность вероятности распределения частиц(рис23)

По физическому смыслу квадрат модуля собственной функции – это плотность вероятности распределения частиц по пространству. В низшем состоянии с наибольшей вероятностью можно найти частицу около середины ящика; вероятность найти ее у стенок равна нулю.

Этот результат резко отличается от классического: в классической механике нахождение частицы в ящике с зеркальными стенками равновероятно в любом месте ящика. Однако при больших nмаксимумы кривой располагаются все ближе друг к другу и к стенкам; приn→ ∞ близка к прямой, параллельной осиx, т.е. для большихnполучается распределение, соответствующее классической частице.

10 (2). Простейшие задачи квантовой механики.Прохождение частицы через потенциальный барьер. Туннельный эффект.

Рассмотрим одномерное движение частицы в области(рис24), где существует потенциальный барьер: "ступенька" прямоугольной формы. Направим ось xпо направлению движения частицы. На границе областей 1 и 2 частица либо пройдет через барьер в область 2, либо отразится и будет двигаться в область 1 в противоположном направлении. Если слева направо движется поток частиц, то часть из них пройдет через барьер, а часть отразится. Задача заключается в определении вероятностей прохождения и отражения частицы при прохождении через барьер.

Вклассической механике если кинетическая энергия частицы больше высоты барьера:T=E>U0, то частица преодолевает барьер с достоверностью. В квантовой механике это не так: частица может отразиться от барьера с некоторой вероятностьюR≠0. В классической механике приE<U0 переход частицы из области 1 в область 2 невозможен: отражение с достоверностью происходит на границе областей. В квантовой механике имеется вероятность найти частицу в области 2. Докажем это, найдем эти вероятности и соответствующие коэффициенты отражения и прохождения (прозрачности).

Запишем уравнение Шредингера: , где

Найдем решения отдельно в области 1 и 2, а затем, используя условие непрерывности, согласуем эти решения (“сошьем”) между собой.

В области 1: (10.1)

В области 2: (10.2)

Обозначим: (10.3)

Т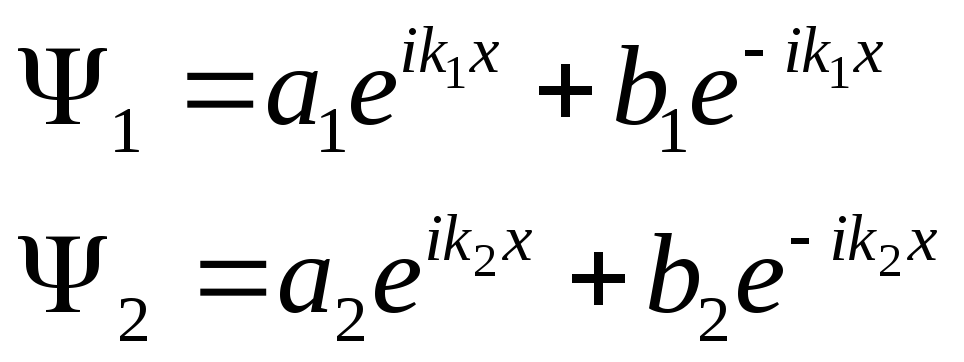огда записанные уравнения принимают вид: (10.4)

а их общие решения:

(10.5)

a1 – амплитуда падающей волны, в области 1,b1– амплитуда отраженной волны, в области 1,a2 – амплитуда прошедшей волны, в области 2,b2– амплитуда отраженной волны, в области 2.

Врассматриваемой задаче частицы, прошедшие в область 2, при движении в этой области никаких препятствий не встречают, поэтому отраженного потока в этой области быть не должно, значит амплитуда отраженной волны в области 2 должна равняться нулю:b2= 0.

Амплитуды b1иa2 найдем из условий непрерывности приx=0:

(10.6)→

Решая относительно b1иa2находим:

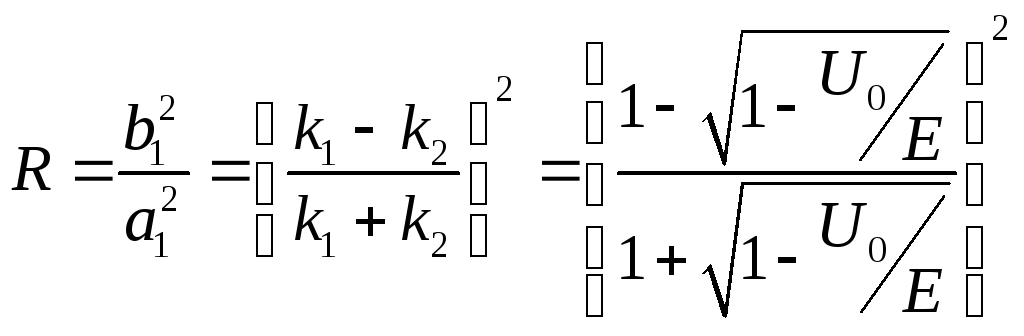(10.7)

Отсюда коэффициент отражения: (10.8)

Для определения коэффициента прохождения

(прозрачности) учтем различные скорости частицы в областях 1 и 2:

З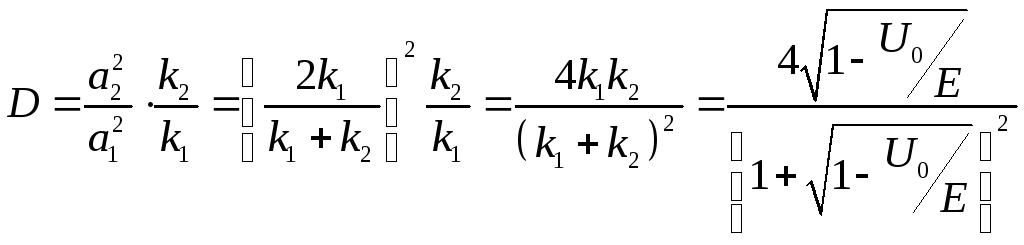десь и - потоки в областях 1 и 2. Поэтому коэффициент прозрачности:

(10.9)

Очевидно, D+R=1, т.е. частица либо отражается, либо преодолевает барьер, как и должно быть. В классической механике приE>U0 частица преодолевает барьер с достоверностью. В квантовой механике это не так: частица может отразиться от барьера и в этом случае (с некоторой вероятностьюR≠0). В классической механике приE<U0 переход частицы из области 1 в область 2 невозможен: отражение с достоверностью происходит на границе областей. В квантовой механике имеется вероятность найти частицу в области 2. Действительно, в этом случае

Отсюда вероятность найти частицу в области 2 равна:

(10.10)→

В то же время коэффициент отражения при E<U0 равен:

(10.11)→

Это означает, что отражение является полным, но не обязательно происходит на самой границе областей: некоторые частицы заходят в область 2, а затем возвращаются в область 1.

Рассмотрим теперь прохождение частиц через прямоугольный потенциальный барьер конечной ширины d:(рис25)

Отличие от предыдущей задачи состоит в том, что отражение происходит на двух границах: 1-2 и 2-3. Поэтому:

Как и в предыдущей задаче, из условий непрерывности ψ и ψ’ на границах, т.е. приx=0 иx=dможно найти коэффициентыb1,a1,b2,a3. Наиболее интересен коэффициентa3– амплитуда прошедшей волны. Вычисления дают:

Коэффициент прозрачности барьера при E<U0 равен:

(10.12)

где

Во многих практически интересных случаях kd>>1, тогда формула дляDупрощается:

(10.13) т.к.

Таким образом, частица с энергией E<U0 может пройти “сквозь” барьер. Вероятность этогоD(проницаемость, прозрачность барьера) сильно зависит от его ширины (dв показателе экспоненты).

Явление прохождения частицы сквозь потенциальный барьер называется туннельным эффектом; при прохождении “сквозь” барьер частица не теряет энергию, она выходит из барьера с той же энергией, с какой в него попадает. Туннельный эффект объясняет многие явления, невозможные с точки зрения классической механики (например, альфа-распад), а также используется в электронных приборах (туннельные диоды, полевые транзисторы).

Мы рассмотрели потенциальный барьер упрощенной прямоугольной формы. Однако, полученный результат легко обобщить на любую форму барьера: достаточно представить его в виде последовательности узких прямоугольных барьеров.

Тогда

(10.14)