8 (2). Уравнение Шредингера.

Н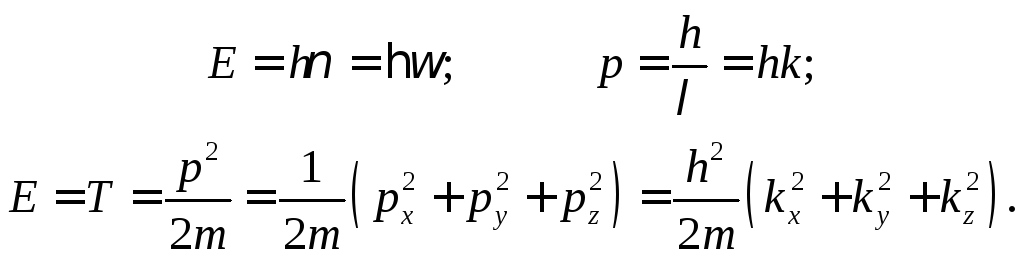айдем уравнение, которому подчиняются волны де-Бройля. Сначала рассмотрим свободную нерелятивистскую частицу. Для такой частицы имеются соотношения:

Сравнивая оба выражения дляE, находим

(8.1)

Свободной частице соответствует плоская волна де-Бройля:

Продифференцируем эту формулу поt,x,y,z:

ивыразим отсюдаn,kx,ky,kz

П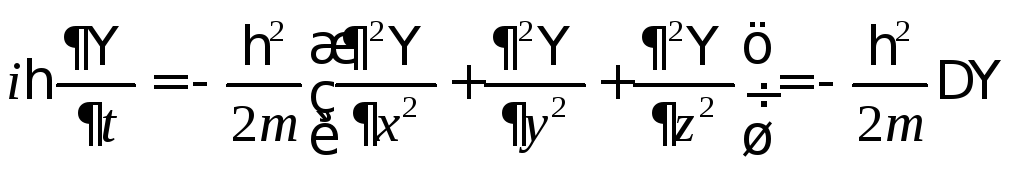одставляя это в формулу (8.1), получаем: или

Это и есть искомое волновое уравнение для свободной нерелятивистской частицы (уравнение Шредингера в простейшей форме):

(8.2)

Для частицы, движущейся в потенциальном поле кинетическая энергияT=E-U, поэтому уравнение (8.2) должно быть записано (обобщено) в виде: (8.3)

Это и есть общее нестационарное (содержащее время) уравнение Шредингера (SchrödingerE., 1926 г.) для частицы в потенциальном полеU.

Зависимость волновой функции от времени выражается множителем:

Поэтому волновая функция может быть представлена в виде

откуда (8.4)

Подставляя (8.4) в (8.2) и (8.3), находим: и

Это стационарное (не зависящее явно от времени) уравнение Шредингера для свободной частицы и для частицы в потенциальном поле U.

Итак, запишем еще раз все четыре формы уравнения Шредингера:

Нестационарное (8.2)

для свободной частицы

Нестационарное для

частицы в потенциаль- (8.3)

ном поле U

Стационарное (8.5)

для свободной частицы

Стационарное для

частицы в потенциаль- (8.6)

ном поле U

Приведенные рассуждения следует рассматривать как пояснения к тому, каким образом было установлено уравнение Шредингера, но не как “вывод” этого уравнения. Как и все основные уравнения физики (уравнения Ньютона, Максвелла и т.д.), уравнение Шредингера не “выводится”, а устанавливается, являясь, по существу, обобщением опытных фактов. Справедливость этого уравнения подтверждается согласием результатов, получаемых с его помощью, с данными экспериментов. Уравнение Шредингера содержит первую производную по времени и вторые по координатам. Поэтому никаких реальных волн, распространяющихся в физической среде, оно не описывает. Это еще один аргумент против гипотезы волнового пакета и подтверждение статистической интерпретации волновой функции:

Терминология

Уравнение Шредингера в зависимости от вида функции Uможет иметь решения, удовлетворяющие естественным условиям (конечности, однозначности, непрерывности, нормировки) либо при любых значенияхE, либо лишь при некоторых дискретных значенияхE.

Те значения E, при которых уравнение Шредингера имеет решение, называются собственными значениями.

Совокупность собственных значений образует энергетический спектр; он может быть непрерывным (если решения есть при любом E), или дискретным. Если движение частицы не ограничено в пространстве, то ее энергетический спектр непрерывен, в противном случае спектр дискретен. Функция Y(x,y,z), являющаяся решением уравнения при данном значении E называется собственной функцией, соответствующей данному собственному значению E.